决策树学习(上)——深度原理剖析及源码实现
引言
本文给大家分享的主题是决策树(Decision Tree)的原理剖析并附上代码实现供大家参考。由于基于决策树的算法较多,因此文章分为上下篇。上篇主要剖析决策树原理、需要掌握的信息论知识以及Java源码实现等内容。下篇内容包括基于决策树的ID3、CART以及C4.5等著名算法的深入比较、理解以及完整代码实现。
决策树是数据挖掘以及机器学习领域一个基础的算法。在此基础上产生诸多著名算法如ID3,CART以及C4.5等。其中C4.5更是被评为数据挖掘领域的十大经典算法。
原理剖析
示例
顾名思义,决策树是一颗关于决策的树。举个简单的例子稍作解释,当我们打算去某家餐厅吃饭的时候会有诸多因素影响我们的决定,例如“当前餐厅的顾客多不多?”、“去餐厅的交通路况如何?”、“餐厅类型,中式、法式还是意式?”等等。在这一系列的一步步的思考之后我们会做出最终的决策:去或者不去该餐厅吃饭。当然也可以在考虑某一个或者部分因素之后做出决策,例如对于某些单身汪“是否有异性相约”是一个无比重要的决策因素,那么对于这些人只考虑一个因素便可以做出最终决策。
我们一起再来看一个例子,银行在放贷款的时候经常会对借贷人进行综合考量,最终做出决策是否借贷款给这个人。当然在考核的过程中若有一项重要指标不符合要求,那么也会立即否决而不考虑其他因素。有如下记录(实际中往往比这些数据复杂得多):

上表中的数据记录了银行以往的借贷历史中用户的情况和最后的偿还情况。我们可以得出拥有房产的人一般是能偿还债务的,而没有房产的人则需要再考虑其他因素等结论。因此根据这些数据我们可以构造如下决策树:
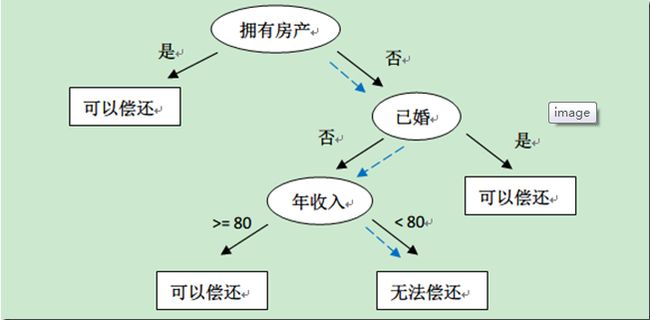
如果此时有一个客户前来贷款,该客户没有房产,单身且年收入只有50K。那么根据上面的决策树,银行可以预测他无法偿还债务(图中蓝色虚线),从而否决对其贷款。此外从上面的决策树,还可以知道是否拥有房产可以在一定程度上决定用户是否可以偿还债务,对借贷业务具有指导意义。
从上面的示例及解释中我们可以总结出如下结论:决策树是一种树形结构,其中每个内部节点表示一个属性上的测试,每个分支代表一个测试输出,每个叶节点代表一种类别。
构造决策树
经过上面的叙述,相信大家已经明白什么是决策树以及决策树的用途,这就解决了我们面对一个新事物时的三要素What,Why and How中的What和Why。那么如何构造一颗决策树呢(How)?这是我们的核心问题。在继续叙述之前,我们需要掌握一些信息论的基础知识。
信息论基础知识
1、熵(entropy)
在信息论里熵叫作信息量,即熵是对不确定性的度量。从控制论的角度来看,应叫不确定性。信息论的创始人香农在其著作《通信的数学理论》中提出了建立在概率统计模型上的信息度量。他把信息定义为“用来消除不确定性的东西”。在信息世界,熵越高,则能传输越多的信息,熵越低,则意味着传输的信息越少(什么鬼,大家可以忽略上述解释,咬文嚼字什么的最烦了)。还是举例说明,假设Kathy在买衣服的时候有颜色,尺寸,款式以及设计年份四种要求,而North只有颜色和尺寸的要求,那么在购买衣服这个层面上Kathy由于选择更多因而不确定性因素更大,最终Kathy所获取的信息更多,也就是熵更大。所以信息量=熵=不确定性,通俗易懂。在叙述决策树时我们用熵表示不纯度(Impurity)。
根据上面的叙述,可以给出如下熵的数学表达式(定义0*log(0)=0):

当然,这个表达式也可以用来量化不纯度。依旧举例解释一下,以前面的去餐厅吃饭为例说明。假设现在有两个独立的决策条件:1.餐厅中顾客数(Patrons),没有、有一些、满员;2.餐厅类型,法式、意式、泰式以及快餐厅。我们现在拥有12名顾客(正负样本各一半)的决策数据,如下图所示(绿色代表正样本,红色代表负样本):

对于这两种决策条件,在决策之前数据集的熵Entropy=H(N)=-(0.5*log(0.5) + 0.5*log(0.5) )=1。我们说此时的熵值最大,也就是说不纯度最小。若数据集中只有一类数据则不纯度最小,即数据是“纯的”。例如在第一种决策中,当餐厅中没有顾客(None)的时候,最终的决策是都不去该餐厅(有可能是该餐厅食物太难吃)。此时熵Entropy=H(N)=-(0*log(0) + 1*log(1))=0。我们说此时数据集不纯度最低,即数据是纯的。
此外,学术界也用基尼系数(Gini):
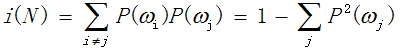
以及误差不纯度:
![]()
来度量不纯度。以上三种方式中通常情况下选用熵作为度量不纯度的指标。
2、信息增益(Information Gain)
数据集的一个属性的信息增益就是由于使用这个属性分割样例而导致的期望熵降低。也就是训练集D分割之前的信息熵减去依据某个属性A分割成若干个子集后的信息熵。其数学表达式为:

举例说明。在上述决策是否去餐厅吃饭的示例中,原数据集的熵为Entropy=H(6/12, 6/12)=1,在两种不同条件下的信息增益分别为:
Gain(Patrons)=1-[2/12H(0,1) + 4/12H(1,0) + 6/12H(2/6, 4/6)]=0.0541
Gani(Type)=1-[2/12H(1/2, 1/2) + 2/12H(1/2, 1/2) + 4/12H(2/4, 2/4) + 4/12H(2/4, 2/4)]=0
因此选用餐厅中顾客数为决策条件能获得的信息增益更大。信息增益越大意味着能将数据集划分得越简洁。通俗地解释,信息增益越大,在同一条件下子集的熵越小,亦即子集越“纯”。这也就是ID3算法的原理。
3、信息增益率(Information Gain Ratio)
历史的进程往往伴随着新的事物推翻旧的事物。ID3于1975年发明,而在1993年被更好的C4.5算法取代。
首先给出信息增益率的数学表达式:
![]()
其中SplitInformation的数学表达式如下所示,其意义为根据属性A划分的各子集所需要的信息量——熵。(有些晦涩,稍后举例说明)
![]()
之所以信息增益率作为划分数据的一种方式出现是由于信息增益 具有倾向于选择划分值多的属性的缺陷。举一个极端例子说明,在上述餐厅示例中,若以餐厅类别为决策条件,并且有12个类别,假设最终每个类别中均只有一个潜在客户的决策。那么此时每个子集中的熵都为0,信息增益增益最大,这样训练出来的决策树往往会导致过拟合。
我们以上述餐厅示例中的第一种情况为例,计算信息增益率。前面我们已经计算过Gain(Patrons)=0.0541,下面计算
SplitInformation(S,Patrons)=-(2/12*log(2/12) + 4/12*log(4/12) + 6/12*log(6/12))=0.7887,
GainRatio(S,Patrons)=Gain(Patrons)/SplitInformation(S,Patrons)=0.0686。
更进一步,信息增益率是如何避免信息增益 中由于优先选择值多的属性而导致过拟合现象的出现?上面我们讨论过以餐厅类型为条件并假设有12种不同餐厅,每类餐厅最后仅有一人做出决策的情况。这种情况下信息增益最大。我们在以顾客数目类型为条件进行决策时,假设仅有两种顾客数目(而不是上述三种类型)——没有顾客(None)以及满员(Full)(并假设数据集均分),并假设此种情况下信息增益略小于餐厅类型的信息增益。那么在算信息增益率的时前者SplitInformation(S,Types)=log(12),后者的SplitInformation(S,Patrons)=1,从而可能出现信息增益虽然前者大,但是信息增益率后者大的情况,这样便可以避免过拟合的出现。C4.5与ID3算法的不同在于C4.5使用信息增益率,而ID3使用信息增益。
当然信息增益率也有其不完美的一面,当某个属性的子集所占数据集的比重非常大的时候,会出现SplitInformation接近0而信息增益率异常大的情况。针对这种种情况可以采取某些处理方法,比如先计算每个属性的增益,然后仅对那些增益高过平均值的属性应用增益比率测试。
再论构造决策树
奥卡姆剃刀定律(Occam’s Razor, Ockham’sRazor)又称“奥康的剃刀”,是由14世纪逻辑学家、圣方济各会修士奥卡姆的威廉(William of Occam,约1285年至1349年)提出。这个原理称为“如无必要,勿增实体”,即“简单有效原理”。正如他在《箴言书注》2卷15题说“切勿浪费较多东西去做,用较少的东西,同样可以做好的事情。”
经过初探信息论 以及掌握一系列数学公式之后,我们继续讨论如何构造决策树。决策树的构造是一个贪心的、递归的、自顶向下的过程。算法选用能将数据集划分最“纯”的节点作为当前节点的子节点(关于熵以及不纯度的知识在上面小节中已经讨论)。决策树构造步骤如下:
- 开始,所有记录看作一个节点
- 遍历每个变量的每一种分割方式,找到最好的分割点
- 分割成两个节点N1和N2
- 对N1和N2分别继续执行2-3步,直到每个节点足够“纯”为止
当每个节点中的记录数小于一个阈值的时候算法停止。需要注意的是当阈值过小,例如为1的时候往往会导致过拟合现象。
剪枝 是解决过拟合的一个有效方法。当树训练得过于茂盛的时候会出现在测试集上的效果比训练集上差不少的现象,即过拟合。可以采用如下两种剪枝策略:
- 前置裁剪 在构建决策树的过程时,提前停止。那么,会将切分节点的条件设置的很苛刻,导致决策树很短小。结果就是决策树无法达到最优。实践证明这种策略无法得到较好的结果。
- 后置裁剪 决策树构建好后,然后才开始裁剪。采用两种方法:1)用单一叶节点代替整个子树,叶节点的分类采用子树中最主要的分类;2)将一个子树完全替代另外一颗子树。当然后置裁剪也同样存在问题,即计算效率,某些节点在计算后被裁剪会导致计算资源浪费,效率偏低。
至此,已经将决策树的原理、构造方法和理解决策树所需要的信息论等知识叙述完。有关基于决策树算法的讲解和代码实现将在《决策树学习(下)》中为大家呈现。
决策树优缺点
通过上面的讨论在这里给出决策树的优缺点。
优点:
- 决策过程接近人的思维习惯。
- 模型容易解释,比线性模型具有更好的解释性。
- 能清楚地使用图形化描述模型。
- 处理定型特征比较容易。
缺点:
- 一般来说,决策树学习方法的准确率不如其他的模型。针对这种情况存在一些解决方案,在后面的文章中为大家讲解。
- 不支持在线学习。当有新样本来的时候,需要重建决策树。
- 容易产生过拟合现象。
决策树实现Java版
import java.util.HashMap;
import java.util.LinkedList;
import java.util.List;
import java.util.Map;
import java.util.Map.Entry;
import java.util.Set;
public class DecisionTree {
public static void main(String[] args) throws Exception {
String[] attrNames = new String[] { "AGE", "INCOME", "STUDENT",
"CREDIT_RATING" };
// 读取样本集
Map> samples = readSamples(attrNames);
// 生成决策树
Object decisionTree = generateDecisionTree(samples, attrNames);
// 输出决策树
outputDecisionTree(decisionTree, 0, null);
}
/**
* 读取已分类的样本集,返回Map:分类 -> 属于该分类的样本的列表
*/
static Map> readSamples(String[] attrNames) {
// 样本属性及其所属分类(数组中的最后一个元素为样本所属分类)
Object[][] rawData = new Object[][] {
{ "<30 ", "High ", "No ", "Fair ", "0" },
{ "<30 ", "High ", "No ", "Excellent", "0" },
{ "30-40", "High ", "No ", "Fair ", "1" },
{ ">40 ", "Medium", "No ", "Fair ", "1" },
{ ">40 ", "Low ", "Yes", "Fair ", "1" },
{ ">40 ", "Low ", "Yes", "Excellent", "0" },
{ "30-40", "Low ", "Yes", "Excellent", "1" },
{ "<30 ", "Medium", "No ", "Fair ", "0" },
{ "<30 ", "Low ", "Yes", "Fair ", "1" },
{ ">40 ", "Medium", "Yes", "Fair ", "1" },
{ "<30 ", "Medium", "Yes", "Excellent", "1" },
{ "30-40", "Medium", "No ", "Excellent", "1" },
{ "30-40", "High ", "Yes", "Fair ", "1" },
{ ">40 ", "Medium", "No ", "Excellent", "0" } };
// 读取样本属性及其所属分类,构造表示样本的Sample对象,并按分类划分样本集
Map> ret = new HashMap>();
for (Object[] row : rawData) {
Sample sample = new Sample();
int i = 0;
for (int n = row.length - 1; i < n; i++)
sample.setAttribute(attrNames[i], row[i]);
sample.setCategory(row[i]);
List samples = ret.get(row[i]);
if (samples == null) {
samples = new LinkedList();
ret.put(row[i], samples);
}
samples.add(sample);
}
return ret;
}
/**
* 构造决策树
*/
static Object generateDecisionTree(
Map> categoryToSamples, String[] attrNames) {
// 如果只有一个样本,将该样本所属分类作为新样本的分类
if (categoryToSamples.size() == 1)
return categoryToSamples.keySet().iterator().next();
// 如果没有供决策的属性,则将样本集中具有最多样本的分类作为新样本的分类,即投票选举出分类
if (attrNames.length == 0) {
int max = 0;
Object maxCategory = null;
for (Entry> entry : categoryToSamples
.entrySet()) {
int cur = entry.getValue().size();
if (cur > max) {
max = cur;
maxCategory = entry.getKey();
}
}
return maxCategory;
}
// 选取测试属性
Object[] rst = chooseBestTestAttribute(categoryToSamples, attrNames);
// 决策树根结点,分支属性为选取的测试属性
Tree tree = new Tree(attrNames[(Integer) rst[0]]);
// 已用过的测试属性不应再次被选为测试属性
String[] subA = new String[attrNames.length - 1];
for (int i = 0, j = 0; i < attrNames.length; i++)
if (i != (Integer) rst[0])
subA[j++] = attrNames[i];
// 根据分支属性生成分支
@SuppressWarnings("unchecked")
Map>> splits =
/* NEW LINE */(Map>>) rst[2];
for (Entry>> entry : splits.entrySet()) {
Object attrValue = entry.getKey();
Map> split = entry.getValue();
Object child = generateDecisionTree(split, subA);
tree.setChild(attrValue, child);
}
return tree;
}
/**
* 选取最优测试属性。最优是指如果根据选取的测试属性分支,则从各分支确定新样本
* 的分类需要的信息量之和最小,这等价于确定新样本的测试属性获得的信息增益最大
* 返回数组:选取的属性下标、信息量之和、Map(属性值->(分类->样本列表))
*/
static Object[] chooseBestTestAttribute(
Map> categoryToSamples, String[] attrNames) {
int minIndex = -1; // 最优属性下标
double minValue = Double.MAX_VALUE; // 最小信息量
Map>> minSplits = null; // 最优分支方案
// 对每一个属性,计算将其作为测试属性的情况下在各分支确定新样本的分类需要的信息量之和,选取最小为最优
for (int attrIndex = 0; attrIndex < attrNames.length; attrIndex++) {
int allCount = 0; // 统计样本总数的计数器
// 按当前属性构建Map:属性值->(分类->样本列表)
Map>> curSplits =
/* NEW LINE */new HashMap>>();
for (Entry> entry : categoryToSamples
.entrySet()) {
Object category = entry.getKey();
List samples = entry.getValue();
for (Sample sample : samples) {
Object attrValue = sample
.getAttribute(attrNames[attrIndex]);
Map> split = curSplits.get(attrValue);
if (split == null) {
split = new HashMap>();
curSplits.put(attrValue, split);
}
List splitSamples = split.get(category);
if (splitSamples == null) {
splitSamples = new LinkedList();
split.put(category, splitSamples);
}
splitSamples.add(sample);
}
allCount += samples.size();
}
// 计算将当前属性作为测试属性的情况下在各分支确定新样本的分类需要的信息量之和
double curValue = 0.0; // 计数器:累加各分支
for (Map> splits : curSplits.values()) {
double perSplitCount = 0;
for (List list : splits.values())
perSplitCount += list.size(); // 累计当前分支样本数
double perSplitValue = 0.0; // 计数器:当前分支
for (List list : splits.values()) {
double p = list.size() / perSplitCount;
perSplitValue -= p * (Math.log(p) / Math.log(2));
}
curValue += (perSplitCount / allCount) * perSplitValue;
}
// 选取最小为最优
if (minValue > curValue) {
minIndex = attrIndex;
minValue = curValue;
minSplits = curSplits;
}
}
return new Object[] { minIndex, minValue, minSplits };
}
/**
* 将决策树输出到标准输出
*/
static void outputDecisionTree(Object obj, int level, Object from) {
for (int i = 0; i < level; i++)
System.out.print("|-----");
if (from != null)
System.out.printf("(%s):", from);
if (obj instanceof Tree) {
Tree tree = (Tree) obj;
String attrName = tree.getAttribute();
System.out.printf("[%s = ?]\n", attrName);
for (Object attrValue : tree.getAttributeValues()) {
Object child = tree.getChild(attrValue);
outputDecisionTree(child, level + 1, attrName + " = "
+ attrValue);
}
} else {
System.out.printf("[CATEGORY = %s]\n", obj);
}
}
/**
* 样本,包含多个属性和一个指明样本所属分类的分类值
*/
static class Sample {
private Map attributes = new HashMap();
private Object category;
public Object getAttribute(String name) {
return attributes.get(name);
}
public void setAttribute(String name, Object value) {
attributes.put(name, value);
}
public Object getCategory() {
return category;
}
public void setCategory(Object category) {
this.category = category;
}
public String toString() {
return attributes.toString();
}
}
/**
* 决策树(非叶结点),决策树中的每个非叶结点都引导了一棵决策树
* 每个非叶结点包含一个分支属性和多个分支,分支属性的每个值对应一个分支,该分支引导了一棵子决策树
*/
static class Tree {
private String attribute;
private Map children = new HashMap();
public Tree(String attribute) {
this.attribute = attribute;
}
public String getAttribute() {
return attribute;
}
public Object getChild(Object attrValue) {
return children.get(attrValue);
}
public void setChild(Object attrValue, Object child) {
children.put(attrValue, child);
}
public Set 参考文献及推荐阅读
- 机器学习,Tom M.Mitchhell著;
- 数据挖掘概念与技术,[美] Micheling Kamber/ Jian Pei 等著;
- 统计学习方法,李航著;
- http://blog.csdn.net/v_july_v/article/details/7577684
- http://www.cnblogs.com/bourneli/archive/2013/03/15/2961568.html
(by希慕,新浪微博:@希慕_North)