数据结构与算法笔记 —— 排序算法及代码实现
数据结构与算法笔记 —— 排序算法及代码实现
一. 直接插入排序
直接插入排序是向一个已经排序好的序列中插入一个数,但是,插入此数后,序列的仍然有序。改算法的时间复杂度为 O(n2) ,时间复杂度较高。适合小规模排序。
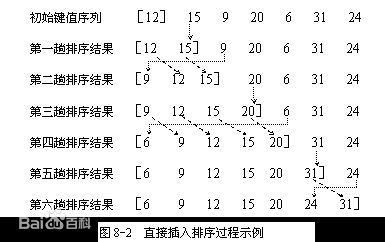
插入排序的基本思想是:每步将一个待排序的纪录,按其关键码值的大小插入前面已经排序的文件中适当位置上,直到全部插入完为止。过程如下图
// c/c++
void InsertSort(int *num,int length){
int t;
for (int i=1;iint j = i-1;
while(j>=0 && t < num[j]){
num[j+1] = num[j];
j--;
}
num[j+1] = t;
}
} 二. 冒泡排序算法
冒泡排序的时间复杂度为 O(n2) ,冒泡排序算法的运作如下:
1. 比较相邻的元素。如果第一个比第二个大,就交换他们两个。
2. 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。在这一点,最后的元素应该会是最大的数。
3. 针对所有的元素重复以上的步骤。
4. 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
// c/c++
void BubbleSort(int *num,const int length){
int tmp;
for (int i=0;ifor(int j=i+1;jif (num[i]>num[j]){
tmp = num[i];
num[i] = num[j];
num[j] = tmp;
}
}
}
} 三. 希尔排序
希尔排序是一种插入排序,它是将整个有序序列分割成若干小的子序列分别进行插入排序,使用增量分组的思想进行排序。
排序过程:先取一个正整数 d1<n , 把所有序号相隔 d1 的数组元素放一组,组内进行直接插入排序,然后取 d2<d2 ,重复上述分组和排序操作;直至 di=1 ,即所有记录放进一个组中排序为止,希尔排序的时间复杂度为 O(n1.2) 。
// c/c++
void ShellSort(int *num,int length){
int l = length/2;
while(l){
//轮换组数
for (int i=l;i//插入排序
int t=num[i];
int m =i-l;
while(m>=0 && tcontinue;
}
num[m+l] = t;
}
l >>=1;
}
} 四. 选择排序
核心思想:减而治之。在一趟扫描后,找出最小的项,放在最前面并将该项去除,从而降低数据项长度,形成新的数据链继续进行。算法时间复杂度 O(n2) 。
// c/c++
void ChooseSort(int *num,int length){
int m=0;
for (int i=0;ifor(int j=i+1;jif (num[j]int t =0;
t = num[i];
num[i] = num[m];
num[m] = t;
}
} 五. 快速排序
排序思想:每进行一次遍历都将比关键值大的数放在关键值后面,比关键值小的数放在关键值前面。然后分成两组进行递归。其算法时间复杂度为$O(n^{
2})$。
// c/c++
void QuickSort(int *num,int left,int right){
if(left >= right){
return;
}
int j = right;
int i = left;
int k = num[left];
while(iwhile(iwhile(i= num[i]) i++;
num[j] = num[i];
}
num[i] = k;
QuickSort(num,left,i-1);
QuickSort(num,i+1,right);
}
六. 归并排序
核心思想:如下图,将数组全部分开,然后两两合并。算法时间复杂度 O(nlogn)
// c/c++
void MergeSort(int *num,int *temp,int start,int middle,int end){
int i = start;
int j = middle+1;
int k = start;
while(i != middle+1 && j!=end+1){
if(num[i]>= num[j]) temp[k++] = num[j++];
else temp[k++] = num[i++];
}
while(i != middle+1) temp[k++] = num[i++];
while(j != end+1) temp[k++] = num[j++];
for(i=start;i<=end;i++)num[i]=temp[i];
}
void Merge11(int *num,int *temp,int start,int end){
int middle = 0;
if(start < end){
middle = (start+end)/2;
Merge11(num,temp,start,middle);
Merge11(num,temp,middle+1,end);
MergeSort(num,temp,start,middle,end);
}
}
