CenterNet之loss计算代码解析

[GiantPandaCV导语] 本文主要讲解CenterNet的loss，由偏置部分（reg loss）、热图部分(heatmap loss)、宽高(wh loss)部分三部分loss组成，附代码实现。

1. 网络输出

论文中提供了三个用于目标检测的网络，都是基于编码解码的结构构建的。

1. ResNet18 + upsample + deformable convolution : COCO AP 28%/142FPS
2. DLA34 + upsample + deformable convolution : COCO AP 37.4%/52FPS
3. Hourglass104: COCO AP 45.1%/1.4FPS

这三个网络中输出内容都是一样的，80个类别，2个预测中心对应的长和宽，2个中心点的偏差。

# heatmap 输出的tensor的通道个数是80，每个通道代表对应类别的heatmap
(hm): Sequential(
(0): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(1): ReLU(inplace)
(2): Conv2d(64, 80, kernel_size=(1, 1), stride=(1, 1))
)
# wh 输出是中心对应的长和宽，通道数为2
(wh): Sequential(
(0): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(1): ReLU(inplace)
(2): Conv2d(64, 2, kernel_size=(1, 1), stride=(1, 1))
)
# reg 输出的tensor通道个数为2，分别是w,h方向上的偏移量
(reg): Sequential(
(0): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(1): ReLU(inplace)
(2): Conv2d(64, 2, kernel_size=(1, 1), stride=(1, 1))
)

2. 损失函数

2.1 heatmap loss

输入图像$I\in R^{W\times H\times 3}$, W为图像宽度，H为图像高度。网络输出的关键点热图heatmap为$\hat{Y}\in [0,1{]}^{\frac{W}{R}\times \frac{H}{R}\times C}$其中，R代表得到输出相对于原图的步长stride。C代表类别个数。

下面是CenterNet中核心loss公式：

$$L_k=\frac{-1}{N}\sum _{xyc}\{\begin{array}{ll}(1-{\hat{Y}}_{xyc}{)}^{\alpha }log({\hat{Y}}_{xyc})& Y_{xyc}=1\\ (1-Y_{xyc}{)}^{\beta }({\hat{Y}}_{xyc}{)}^{\alpha }log(1-{\hat{Y}}_{xyc})& otherwise\end{array}$$

这个和Focal loss形式很相似，$\alpha$和$\beta$是超参数，N代表的是图像关键点个数。

• 在$Y_{xyc}=1$的时候，

对于易分样本来说，预测值${\hat{Y}}_{xyc}$接近于1，$(1-{\hat{Y}}_{xyc}{)}^{\alpha }$就是一个很小的值，这样loss就很小，起到了矫正作用。

对于难分样本来说，预测值${\hat{Y}}_{xyc}$接近于0，$ (1-\hat{Y}_{xyc})^\alpha$就比较大，相当于加大了其训练的比重。

• otherwise的情况下：

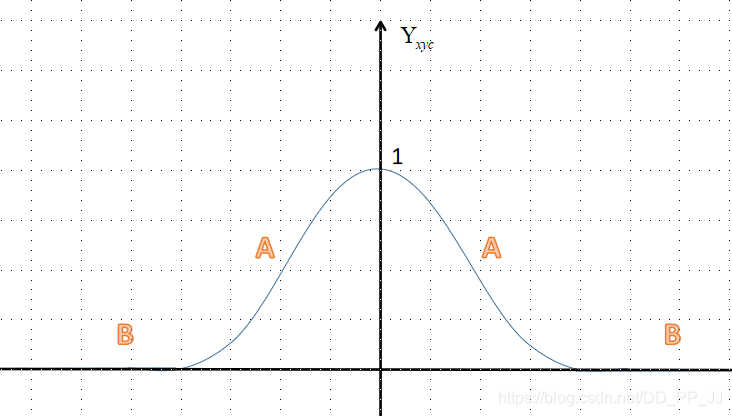
上图是一个简单的示意，纵坐标是$Y_{xyc}$，分为A区（距离中心点较近，但是值在0-1之间）和B区（距离中心点很远接近于0）。

对于A区来说，由于其周围是一个高斯核生成的中心，$Y_{xyc}$的值是从1慢慢变到0。

举个例子(CenterNet中默认$\alpha =2,\beta =4$)：

$Y_{xyc}=0.8$的情况下，

• 如果${\hat{Y}}_{xyc}=0.99$，那么loss=$(1-0.8{)}^4(0.99{)}^{2}log(1-0.99)$,这就是一个很大的loss值。

• 如果${\hat{Y}}_{xyc}=0.8$, 那么loss=$(1-0.8{)}^4(0.8{)}^{2}log(1-0.8)$, 这个loss就比较小。

• 如果${\hat{Y}}_{xyc}=0.5$, 那么loss=$(1-0.8{)}^4(0.5{)}^{2}log(1-0.5)$,

• 如果${\hat{Y}}_{xyc}=0.99$，那么loss=$(1-0.5{)}^4(0.99{)}^{2}log(1-0.99)$,这就是一个很大的loss值。

• 如果${\hat{Y}}_{xyc}=0.8$, 那么loss=$(1-0.5{)}^4(0.8{)}^{2}log(1-0.8)$, 这个loss就比较小。

• 如果${\hat{Y}}_{xyc}=0.5$, 那么loss=$(1-0.5{)}^4(0.5{)}^{2}log(1-0.5)$,

总结一下：为了防止预测值${\hat{Y}}_{xyc}$过高接近于1，所以用$({\hat{Y}}_{xyc}{)}^{\alpha }$来惩罚Loss。而$(1-Y_{xyc}{)}^{\beta }$这个参数距离中心越近，其值越小，这个权重是用来减轻惩罚力度。

对于B区来说，${\hat{Y}}_{xyc}$的预测值理应是0，如果该值比较大比如为1，那么$({\hat{Y}}_{xyc}{)}^{\alpha }$作为权重会变大，惩罚力度也加大了。如果预测值接近于0，那么$({\hat{Y}}_{xyc}{)}^{\alpha }$会很小，让其损失比重减小。对于$(1-Y_{xyc}{)}^{\beta }$来说，B区的值比较大，弱化了中心点周围其他负样本的损失比重。

2.2 offset loss

由于三个骨干网络输出的feature map的空间分辨率变为原来输入图像的四分之一。相当于输出feature map上一个像素点对应原始图像的4x4的区域，这会带来较大的误差，因此引入了偏置值和偏置的损失值。设骨干网络输出的偏置值为$\hat{O}\in R^{\frac{W}{R}\times \frac{H}{R}\times 2}$, 这个偏置值用L1 loss来训练：
$$L_{offset}=\frac{1}{N}\sum _p|{\hat{O}}_{\tilde{p}}-(\frac{p}{R}-\tilde{p})|$$
p代表目标框中心点，R代表下采样倍数4，$\tilde{p}=\lfloor \frac{p}{R}\rfloor$, $\frac{p}{R}-\tilde{p}$代表偏差值。

2.3 size loss/wh loss

假设第k个目标，类别为$c_k$的目标框的表示为$(x_1^{(k)},y_1^{(k)},x_2^{(k)},y_2^{(k)})$，那么其中心点坐标位置为$(\frac{x_1^{(k)}+x_2^{(k)}}{2},\frac{y_1^{(k)}+y_2^{(k)}}{2})$, 目标的长和宽大小为$s_k=(x_2^{(k)}-x_1^{(k)},y_2^{(k)}-y_1^{(k)})$。对长和宽进行训练的是L1 Loss函数：
$$L_{size}=\frac{1}{N}\sum _{k=1}^N|{\hat{S}}_{pk}-s_k|$$
其中$\hat{S}\in R^{\frac{W}{R}\times \frac{H}{R}\times 2}$是网络输出的结果。

2.4 CenterNet Loss

整体的损失函数是以上三者的综合，并且分配了不同的权重。
$$L_{det}=L_k+{\lambda }_{size}{L}_{size}+{\lambda }_{offset}{L}_{offset}$$
其中${\lambda }_{size}=0.1,{\lambda }_{offsize}=1$

3. 代码解析

来自train.py中第173行开始进行loss计算：

# 得到heat map, reg, wh 三个变量
hmap, regs, w_h_ = zip(*outputs)

regs = [
_tranpose_and_gather_feature(r, batch['inds']) for r in regs
]
w_h_ = [
_tranpose_and_gather_feature(r, batch['inds']) for r in w_h_
]

# 分别计算loss
hmap_loss = _neg_loss(hmap, batch['hmap'])
reg_loss = _reg_loss(regs, batch['regs'], batch['ind_masks'])
w_h_loss = _reg_loss(w_h_, batch['w_h_'], batch['ind_masks'])

# 进行loss加权，得到最终loss
loss = hmap_loss + 1 * reg_loss + 0.1 * w_h_loss

上述transpose_and_gather_feature函数具体实现如下，主要功能是将ground truth中计算得到的对应中心点的值获取。

def _tranpose_and_gather_feature(feat, ind):
  # ind代表的是ground truth中设置的存在目标点的下角标
  feat = feat.permute(0, 2, 3, 1).contiguous()# from [bs c h w] to [bs, h, w, c] 
  feat = feat.view(feat.size(0), -1, feat.size(3)) # to [bs, wxh, c]
  feat = _gather_feature(feat, ind)
  return feat

def _gather_feature(feat, ind, mask=None):
  # feat : [bs, wxh, c]
  dim = feat.size(2)
  # ind : [bs, index, c]
  ind = ind.unsqueeze(2).expand(ind.size(0), ind.size(1), dim)
  feat = feat.gather(1, ind) # 按照dim=1获取ind
  if mask is not None:
    mask = mask.unsqueeze(2).expand_as(feat)
    feat = feat[mask]
    feat = feat.view(-1, dim)
  return feat

3.1 hmap loss代码

调用：hmap_loss = _neg_loss(hmap, batch['hmap'])

def _neg_loss(preds, targets):
    ''' Modified focal loss. Exactly the same as CornerNet.
        Runs faster and costs a little bit more memory
        Arguments:
        preds (B x c x h x w)
        gt_regr (B x c x h x w)
    '''
    pos_inds = targets.eq(1).float()# heatmap为1的部分是正样本
    neg_inds = targets.lt(1).float()# 其他部分为负样本

    neg_weights = torch.pow(1 - targets, 4)# 对应(1-Yxyc)^4

    loss = 0
    for pred in preds: # 预测值
        # 约束在0-1之间
        pred = torch.clamp(torch.sigmoid(pred), min=1e-4, max=1 - 1e-4)
        pos_loss = torch.log(pred) * torch.pow(1 - pred, 2) * pos_inds
        neg_loss = torch.log(1 - pred) * torch.pow(pred,
                                                   2) * neg_weights * neg_inds
        num_pos = pos_inds.float().sum()
        pos_loss = pos_loss.sum()
        neg_loss = neg_loss.sum()

        if num_pos == 0:
            loss = loss - neg_loss # 只有负样本
        else:
            loss = loss - (pos_loss + neg_loss) / num_pos
    return loss / len(preds)

$$L_k=\frac{-1}{N}\sum _{xyc}\{\begin{array}{ll}(1-{\hat{Y}}_{xyc}{)}^{\alpha }log({\hat{Y}}_{xyc})& Y_{xyc}=1\\ (1-Y_{xyc}{)}^{\beta }({\hat{Y}}_{xyc}{)}^{\alpha }log(1-{\hat{Y}}_{xyc})& otherwise\end{array}$$

代码和以上公式一一对应，pos代表正样本，neg代表负样本。

3.2 reg & wh loss代码

调用：reg_loss = _reg_loss(regs, batch['regs'], batch['ind_masks'])

调用：w_h_loss = _reg_loss(w_h_, batch['w_h_'], batch['ind_masks'])

def _reg_loss(regs, gt_regs, mask):
    mask = mask[:, :, None].expand_as(gt_regs).float()
    loss = sum(F.l1_loss(r * mask, gt_regs * mask, reduction='sum') /
               (mask.sum() + 1e-4) for r in regs)
    return loss / len(regs)

4. 参考

https://zhuanlan.zhihu.com/p/66048276

http://xxx.itp.ac.cn/pdf/1904.07850