Python实战笔记(四) 正方体展开图自动出题
0、需求说明
最近笔者遇到一个需求,那就是自动生成正方体展开图的问题,要求生成的问题必须保证正确性与随机性
相信大家或多或少都有接触过这样的问题,这类型的问题主要考察的是做题者的空间推理能力
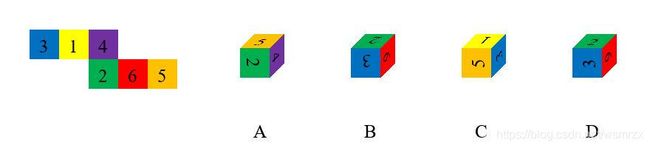
一个问题包含三个基本要素:题目、选项(包括正确答案与干扰项)、答案,最终效果如下:
题目:以下左图是正方体外表面的展开图,请问右边哪一项可以由它折叠而成?
答案:C
下面首先会讲解如何生成一道正确的问题,然后介绍怎么将问题转换成图片,最后会贴出完整的代码
不想看过程的朋友,可以直接拖动到最后的代码部分,开箱即用,下面让我们开始吧
PS:由于笔者能力和时间有限,若代码或结果中出现错误,欢迎大家指正!
1、逻辑部分
基本思路:
1、首先预定义好所有可能的正方体展开图,在生成问题时随机选择一种作为题目
2、然后对每一种正方体展开图预定义其中一种还原形态(正方体,过渡变量)
3、最后根据还原形态的正方体,通过旋转变换生成选项(三视图)
业务逻辑与用户界面分离,在日常开发中是一个很重要的准则
下面我们先来解决一个问题,即在不考虑如何画图的情况下,怎么生成一道正方体展开图的问题
(1)展开图到正方体的映射
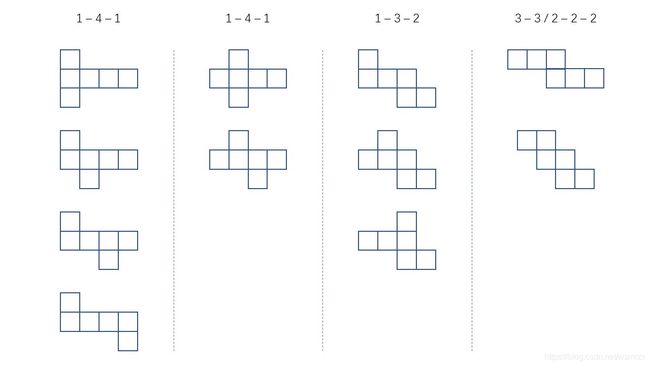
首先我们知道,一个正方体的展开图只有有限种情况,具体来说有 11 种,列举如下:
然后我们给正方体展开图中的每个面编个号,并定义其中一种还原状态,用代码表示如下:
# 展开图(题干) -> 正方体
figure2cube = [{
'figure': [
[1, 0, 0, 0, 0],
[2, 3, 4, 5, 0],
[6, 0, 0, 0, 0],
],
'cube': ['1/000', '2/000', '3/000', '4/000', '5/000', '6/180']
}, {
'figure': [
[1, 0, 0, 0, 0],
[2, 3, 4, 5, 0],
[0, 6, 0, 0, 0],
],
'cube': ['1/000', '2/000', '3/000', '4/000', '5/000', '6/270']
}, {
'figure': [
[1, 0, 0, 0, 0],
[2, 3, 4, 5, 0],
[0, 0, 6, 0, 0],
],
'cube': ['1/000', '2/000', '3/000', '4/000', '5/000', '6/000']
}, {
'figure': [
[1, 0, 0, 0, 0],
[2, 3, 4, 5, 0],
[0, 0, 0, 6, 0],
],
'cube': ['1/000', '2/000', '3/000', '4/000', '5/000', '6/090']
}, {
'figure': [
[0, 1, 0, 0, 0],
[2, 3, 4, 5, 0],
[0, 6, 0, 0, 0],
],
'cube': ['1/000', '3/000', '4/000', '5/000', '2/000', '6/180']
}, {
'figure': [
[0, 1, 0, 0, 0],
[2, 3, 4, 5, 0],
[0, 0, 6, 0, 0],
],
'cube': ['1/000', '3/000', '4/000', '5/000', '2/000', '6/270']
}, {
'figure': [
[1, 0, 0, 0, 0],
[2, 3, 4, 0, 0],
[0, 0, 5, 6, 0],
],
'cube': ['1/000', '2/000', '3/000', '4/000', '6/270', '5/000']
}, {
'figure': [
[0, 1, 0, 0, 0],
[2, 3, 4, 0, 0],
[0, 0, 5, 6, 0],
],
'cube': ['1/000', '3/000', '4/000', '6/270', '2/000', '5/270']
}, {
'figure': [
[0, 0, 1, 0, 0],
[2, 3, 4, 0, 0],
[0, 0, 5, 6, 0],
],
'cube': ['1/000', '4/000', '6/270', '2/000', '3/000', '5/180']
}, {
'figure': [
[1, 2, 3, 0, 0],
[0, 0, 4, 5, 6],
[0, 0, 0, 0, 0],
],
'cube': ['1/000', '4/180', '2/090', '6/180', '5/180', '3/000']
}, {
'figure': [
[1, 2, 0, 0, 0],
[0, 3, 4, 0, 0],
[0, 0, 5, 6, 0],
],
'cube': ['1/000', '3/090', '2/090', '6/180', '5/180', '4/270']
}]
其中,figure 表示正方体展开图,数字 0 不表示内容,数字 1~ 6 分别表示六个展开面
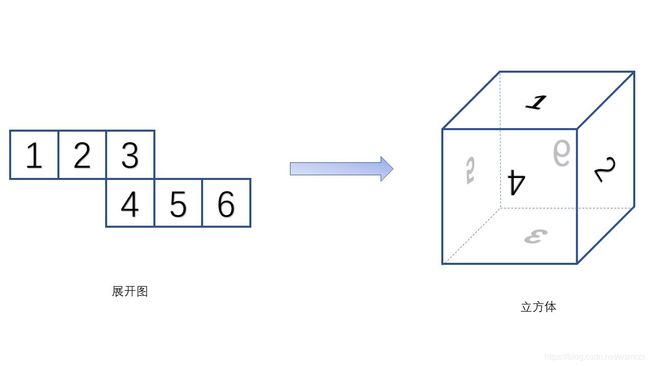
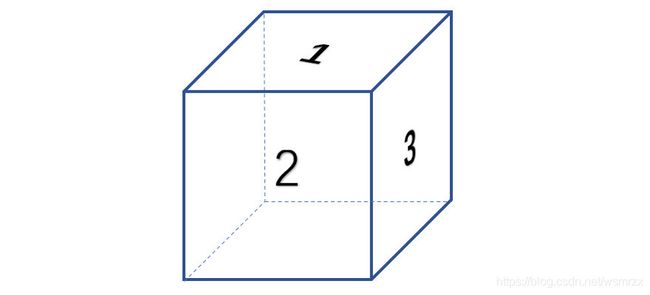
cube 表示折叠后的正方体,cube 中六个元素分别表示正方体的六个面,对应关系如下图所示:
cube 的值是统一的格式 s/aaa,s 表示对应展开图的哪个面,aaa 表示那个面顺时针旋转多少度
可能上面的描述不是很直观,下面举一个例子来说明:
{
'figure': [
[1, 2, 3, 0, 0],
[0, 0, 4, 5, 6],
[0, 0, 0, 0, 0],
],
'cube': ['1/000', '4/180', '2/090', '6/180', '5/180', '3/000']
}
figure 表示的展开图很直观,这里不再赘述,重点来看 cube 是怎么对应的
cube 第 1 个元素是 1/000,表示正方体上面由展开图中 1 号面顺时针旋转 0 度而来
cube 第 2 个元素是 4/180,表示正方体前面由展开图中 4 号面顺时针旋转 180 度而来
cube 第 3 个元素是 2/090,表示正方体右面由展开图中 2 号面顺时针旋转 90 度而来
cube 第 4 个元素是 6/180,表示正方体后面由展开图中 6 号面顺时针旋转 180 度而来
cube 第 5 个元素是 5/180,表示正方体左面由展开图中 5 号面顺时针旋转 180 度而来
cube 第 6 个元素是 3/000,表示正方体下面由展开图中 3 号面顺时针旋转 0 度而来
(2)正方体到三视图的映射
经过上面的映射,我们已经可以将展开图还原成一个正方体
接下来,我们要针对一个普通的正方体定义出其所有的三视图(上面、前面、右面)
所幸,给定一个正方体,它的三视图也只有有限种情况,具体来说有 24 种,用代码表示如下:
# 正方体 -> 三视图(选项)
view2cube = [
# 1 为上顶面,6 为下底面
['1/000', '2/000', '3/000'],
['1/090', '3/000', '4/000'],
['1/180', '4/000', '5/000'],
['1/270', '5/000', '2/000'],
# 6 为上顶面,1 为下底面
['6/000', '2/180', '5/180'],
['6/090', '5/180', '4/180'],
['6/180', '4/180', '3/180'],
['6/270', '3/180', '2/180'],
# 2 为上顶面,4 为下底面
['2/000', '6/180', '3/090'],
['2/090', '3/090', '1/180'],
['2/180', '1/180', '5/270'],
['2/270', '5/270', '6/180'],
# 4 为上顶面,2 为下底面
['4/000', '6/000', '5/090'],
['4/090', '5/090', '1/000'],
['4/180', '1/000', '3/270'],
['4/270', '3/270', '6/000'],
# 3 为上顶面,5 为下底面
['3/000', '6/090', '4/090'],
['3/090', '4/090', '1/270'],
['3/180', '1/270', '2/270'],
['3/270', '2/270', '6/090'],
# 5 为上顶面,3 为下底面
['5/000', '6/270', '2/090'],
['5/090', '2/090', '1/090'],
['5/180', '1/090', '4/270'],
['5/270', '4/270', '6/270'],
]
view2cube 变量中有 24 个子列表,其中每个列表代表一种可能的三视图
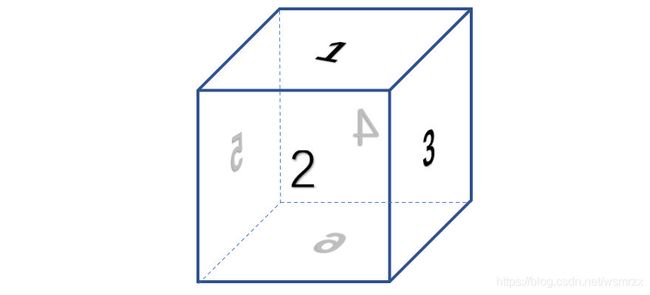
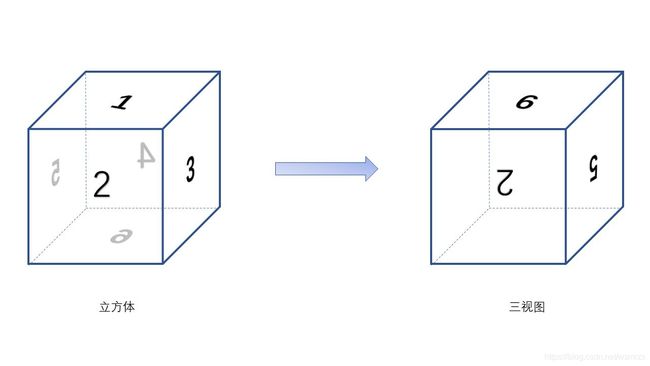
每个子列表有三个元素,分别代表三视图中的三个面,对应关系如下图所示:
元素的值也像上面是一样的格式 s/aaa,s 表示对应正方体的哪个面,aaa 表示那个面顺时针旋转多少度
这里也举一个例子来说明:
['6/000', '2/180', '5/180']
第 1 个元素是 6/000,表示三视图上面由正方体中 6 号面顺时针旋转 0 度而来
第 2 个元素是 2/180,表示三视图前面由正方体中 2 号面顺时针旋转 180 度而来
第 3 个元素是 5/180,表示三视图右面由正方体中 5 号面顺时针旋转 180 度而来
(3)生成问题
最后根据上述的两个对应关系,我们就可以生成题目和选项(包括答案和干扰项)
-
题目的生成逻辑:随机选择一个展开图作为题目
-
答案的生成逻辑:随机选择一个三视图作为答案
-
干扰项生成逻辑:随机选择一个三视图,替换一个面或选择一个面旋转若干角度
详情请看代码中的注释:
def generate_question(config):
# 从 figure2cube 随机选择一项作为题目
f2c = random.choice(figure2cube)
figure = f2c['figure'] # 展开图
cube = f2c['cube'] # 正方体
# 生成答案候选
answers = []
for _ in range(4):
# 从 view2cube 随机选择一项作为答案
v2c = random.choice(view2cube)
ans = []
for c1 in v2c:
s1 = c1.split('/')[0]
a1 = c1.split('/')[1]
c2 = cube[int(s1) - 1]
s2 = c2.split('/')[0]
a2 = c2.split('/')[1]
ans.append(
s2 + '/' + str((int(a1) + int(a2)) % 360).zfill(3)
)
answers.append(ans)
# 将候选答案中的第一项作为正确答案
answer = answers[0]
answer_k = ';'.join(answer)
# 将候选答案中的其余项作为干扰项
option = answers[1:]
for opt in option:
idx = random.choice([1, 2, 3])
isa = random.randint(0, 1)
s = opt[idx - 1].split('/')[0]
a = opt[idx - 1].split('/')[1]
# 替换一个面或选择一个面旋转若干角度
if config['canRotate'] and isa:
a = str((int(a) + random.choice([90, 180, 270])) % 360).zfill(3)
else:
filter_list = [int(opt[idx - 1].split('/')[0]) for idx in [1, 2, 3]]
chosen_list = list(filter(lambda x : x not in filter_list, [1, 2, 3, 4, 5, 6]))
s = str(random.choice(chosen_list))
opt[idx - 1] = s + '/' + a
# 合并正确答案和干扰项,得到所有选项
choice = []
choice.append(answer)
choice.extend(option)
random.shuffle(choice)
# 找出正确答案的选项值,得到答案选项
answer_v = ''
for i, c in enumerate(choice):
if answer_k == ';'.join(c):
answer_v = chr(i + 65)
break
# 返回结果
return figure, choice, answer_v
2、界面部分
基本思路:
1、首先画出六个小正方形分别作为正方体的六个面
2、根据六个正方形和题目(正方体展开图)的表示画出题目
3、根据六个正方形和选项(正方体三视图)的表示画出选项
4、将题目和选项拼接起来得到完整的问题
(1)画六个正方形
def draw_squares(config, side_len):
color = [(255, 0, 0), (255, 192, 0), (255, 255, 0), (0, 176, 80), (0, 112, 192), (112, 48, 160)]
random.shuffle(color)
border_width = 1
fills = [] # 作为填充的正方形
for i in range(6):
fill = Image.new('RGB', (side_len - border_width * 2, side_len - border_width * 2), color[i] if config['hasColor'] else (255, 255, 255))
fills.append(fill)
# 给正方形添加内容
draw_fills(config, fills)
squares = [] # 带有边框的正方形
for i in range(6):
background = Image.new('RGB', (side_len, side_len), color[i] if config['hasColor'] else (0, 0, 0))
background.paste(fills[i], (border_width, border_width, side_len - border_width, side_len - border_width))
squares.append(background)
return squares
给正方形添加内容,可选形状包括:数字、点(仿骰子)、线、面(三角形)
def draw_fills(config, fills):
pattern = config['pattern']
fillW, fillH = fills[0].size
if pattern == 'number': # 数字
order = [1, 2, 3, 4, 5, 6]
random.shuffle(order)
for idx, sur in enumerate(fills):
draw = ImageDraw.Draw(sur)
text = str(order[idx])
draw_ttf = ImageFont.truetype('times.ttf', 25)
ttfW, ttfH = draw_ttf.getsize(text)
draw_poX = (fillW - ttfW) // 2
draw_poY = (fillH - ttfH) // 2
draw.text((draw_poX, draw_poY), text, font = draw_ttf, fill = (0, 0, 0))
elif pattern == 'dot': # 点 (仿骰子)
order = [1, 2, 3, 4, 5, 6]
random.shuffle(order)
radius = 4
gapping = 2
direction = [
[
[fillW // 2 - radius, fillH // 2 - radius, fillW // 2 + radius, fillH // 2 + radius]
],
[
[fillW // 2 - radius, fillH // 2 - radius * 2 - gapping // 2, fillW // 2 + radius, fillH // 2 - gapping // 2],
[fillW // 2 - radius, fillH // 2 + gapping // 2, fillW // 2 + radius, fillH // 2 + gapping // 2 + radius * 2],
],
[
[fillW // 2 - radius * 3 - gapping, fillH // 2 - radius * 3 - gapping, fillW // 2 - radius - gapping, fillH // 2 - radius - gapping],
[fillW // 2 - radius, fillH // 2 - radius, fillW // 2 + radius, fillH // 2 + radius],
[fillW // 2 + radius + gapping, fillH // 2 + radius + gapping, fillW // 2 + radius * 3 + gapping, fillH // 2 + radius * 3 + gapping],
],
[
[fillW // 2 - gapping // 2 - radius * 2, fillH // 2 - gapping // 2 - radius * 2, fillW // 2 - gapping // 2, fillH // 2 - gapping // 2],
[fillW // 2 + gapping // 2, fillH // 2 - gapping // 2 - radius * 2, fillW // 2 + gapping // 2 + radius * 2, fillH // 2 - gapping // 2],
[fillW // 2 - gapping // 2 - radius * 2, fillH // 2 + gapping // 2, fillW // 2 - gapping // 2, fillH // 2 + gapping // 2 + radius * 2],
[fillW // 2 + gapping // 2, fillH // 2 + gapping // 2, fillW // 2 + gapping // 2 + radius * 2, fillH // 2 + gapping // 2 + radius * 2],
],
[
[fillW // 2 - radius * 3 - gapping, fillH // 2 - radius * 3 - gapping, fillW // 2 - radius - gapping, fillH // 2 - radius - gapping],
[fillW // 2 + radius + gapping, fillH // 2 - radius * 3 - gapping, fillW // 2 + radius * 3 + gapping, fillH // 2 - radius - gapping],
[fillW // 2 - radius, fillH // 2 - radius, fillW // 2 + radius, fillH // 2 + radius],
[fillW // 2 - radius * 3 - gapping, fillH // 2 + radius + gapping, fillW // 2 - radius - gapping, fillH // 2 + radius * 3 + gapping],
[fillW // 2 + radius + gapping, fillH // 2 + radius + gapping, fillW // 2 + radius * 3 + gapping, fillH // 2 + radius * 3 + gapping],
],
[
[fillW // 2 - gapping // 2 - radius * 2, fillH // 2 - radius * 3 - gapping, fillW // 2 - gapping // 2, fillH // 2 - radius - gapping],
[fillW // 2 + gapping // 2, fillH // 2 - radius * 3 - gapping, fillW // 2 + gapping // 2 + radius * 2, fillH // 2 - radius - gapping],
[fillW // 2 - gapping // 2 - radius * 2, fillH // 2 - radius, fillW // 2 - gapping // 2, fillH // 2 + radius],
[fillW // 2 + gapping // 2, fillH // 2 - radius, fillW // 2 + gapping // 2 + radius * 2, fillH // 2 + radius],
[fillW // 2 - gapping // 2 - radius * 2, fillH // 2 + radius + gapping, fillW // 2 - gapping // 2, fillH // 2 + radius * 3 + gapping],
[fillW // 2 + gapping // 2, fillH // 2 + radius + gapping, fillW // 2 + gapping // 2 + radius * 2, fillH // 2 + radius * 3 + gapping],
],
]
for idx, sur in enumerate(fills):
draw = ImageDraw.Draw(sur)
for point in direction[order[idx] - 1]:
draw.ellipse(point, fill = (0, 0, 0))
elif pattern == 'line': # 线
direction = [
(0, 0, fillW, fillH),
(fillW, 0, 0, fillH),
# (fillW // 2, 0, fillW // 2, fillH),
# (0, fillH // 2, fillW, fillH // 2),
]
for idx, sur in enumerate(fills):
draw = ImageDraw.Draw(sur)
draw.line(random.choice(direction), fill = (0, 0, 0))
elif pattern == 'triangle': # 面 (三角形)
tempW, tempH = fillW // 3, fillH // 3
direction = [
(tempW, 2 * tempH, 1.5 * tempW, tempH, 2 * tempW, 2 * tempH),
(tempW, tempH, 1.5 * tempW, 2 * tempH, 2 * tempW, tempH),
(tempW, tempH, 2 * tempW, 1.5 * tempH, tempW, 2 * tempH),
(2 * tempW, tempH, tempW, 1.5 * tempH, 2 * tempW, 2 * tempH),
]
for idx, sur in enumerate(fills):
draw = ImageDraw.Draw(sur)
draw.polygon(random.choice(direction), fill = (0, 0, 0))
else:
raise ValueError()
(2)画题目【正方体展开图】
def draw_figure(figure_data, squares, side_len):
row, col = 3, 5
padding = side_len
cn = -1
figure = Image.new('RGB', (col * side_len + padding * 2, row * side_len + padding * 2), (255, 255, 255))
for i in range(row):
for j in range(col):
if figure_data[i][j] != 0:
cn += 1
figure.paste(squares[cn], (padding + j * side_len, padding + i * side_len, padding + (j + 1) * side_len, padding + (i + 1) * side_len))
return figure
(3)画选项【正方体三视图】
def draw_view(choice_data, squares, square_len):
viewW, choiceW = 150, 150
viewH, choiceH = 150, 50
# 对每个选项遍历
views = []
for choice_idx, choice in enumerate(choice_data):
# 对每个三视图中的面遍历
view = Image.new('RGB', (viewW, viewH + choiceH), (255, 255, 255))
for idx, val in enumerate(choice):
s = val.split('/')[0]
a = val.split('/')[1]
square = squares[int(s) - 1].rotate(360 - int(a))
if idx == 0: # 三视图的上面
px = (viewW - (square_len + square_len // 2)) // 2
py = (viewH - (square_len + square_len // 2)) // 2 + square_len // 2
square = square.resize((square_len, square_len // 2))
matrixV = np.array(view)
matrixS = np.array(square)
for i in range(square_len // 2):
matrixV[py - i, px + i: px + i + square_len] = matrixS[square_len // 2 - i - 1]
view = Image.fromarray(matrixV)
elif idx == 1: # 三视图的前面
px = (viewW - (square_len + square_len // 2)) // 2
py = (viewH - (square_len + square_len // 2)) // 2 + square_len // 2
view.paste(square, (px, py))
elif idx == 2: # 三视图的右面
px = (viewW - (square_len + square_len // 2)) // 2 + square_len
py = (viewH - (square_len + square_len // 2)) // 2 + (square_len + square_len // 2)
square = square.resize((square_len // 2, square_len))
matrixV = np.array(view)
matrixS = np.array(square)
for i in range(square_len // 2):
matrixV[py - square_len - i: py - i, px + i] = matrixS[:, i]
view = Image.fromarray(matrixV)
# 写选项值 (A / B / C / D)
draw = ImageDraw.Draw(view)
draw_ttf = ImageFont.truetype('times.ttf', 25)
draw_poX = choiceW // 2 - 12
draw_poY = viewH + choiceH // 2 - 12
draw.text((draw_poX, draw_poY), chr(choice_idx + 65), font = draw_ttf, fill = (0, 0, 0))
# 得到一个选项的三视图
views.append(view)
# 拼接所有选项的三视图,合成一张图片
data = Image.new('RGB', (viewW * len(views), viewH + choiceH), (255, 255, 255))
for view_idx, view in enumerate(views):
data.paste(view, (view_idx * viewW, 0))
return data
(4)将题目和选项拼接起来
def draw_image(config, figure_data, choice_data):
# 小正方形边长
square_len = 40
# 画六个正方形
squares = draw_squares(config, square_len)
# 画展开图(题目)
figure = draw_figure(figure_data, squares, square_len)
# 画三视图(选项)
view = draw_view(choice_data, squares, square_len)
# 最终图片,拼接题目和选项
final_image = Image.new('RGB', (figure.size[0] + view.size[0], max(figure.size[1], view.size[1])), (255, 255, 255))
final_image.paste(figure, (0, 0))
final_image.paste(view, (figure.size[0], 0))
# 返回结果
return final_image
3、完整代码
完整代码和相关说明文档请移步我的 Github 仓库