算法概论笔记 - 分治法

1. 将原问题分解为一组子问题，每个子问题都与原问题类型相同，但是比原问题的规模小
2. 递归求解这些子问题
3. 将子问题的求解结果恰当合并，得到原问题的解

分治算法更多地是使已经能在多项式时间内解决的问题求解得更快。

二进制乘法

假设x和y是两个n位二进制整数，我们将每个数都一分为二，每个数的左半部分和右半部分都是n/2位二进制数：

(2^{n/2}y_L + y_R) = 2^nx_Ly_L + 2^{n/2}(x_Ly_R + x_Ry_L) + x_Ry_R)

此时，T(n) = 4T(n/2) + O(n)，时间复杂度为O(n^2)

(y_L + y_R) - x_Ly_L - x_Ry_R)

这时，T(n) <= 3T(n/2 + 1) + O(n)，时间复杂度为

矩阵乘法

两个nn的矩阵X和Y的乘积得到另一个nn的矩阵Z=XY

直接计算

时间复杂度= = O(n^3)​)

元素数目*每个元素的计算时间

分治优化

利用矩阵乘法能够分块进行的特性



从而，

其中，
\quad P_2=(A+B)H\quad P_3=(C+D)E\quad P_4=D(G-E)\quad P_5=(A+D)(E+H)\quad P_6=(B-D)(G+H)\quad P_7=(A-C)(E+F))

算法T(n) = 7T(n/2) + O(n^2)，根据主定理可得，

时间复杂度=

递归树视角：

算法的递归调用构成一个树状结构。在深度为k的层次上，共有

个子问题，每一个的规模都是

，该层次花费的时间为

。在

的层次上，子问题的规模降为1，此时^{log_2n}O(n) = 3^{log_2n} = n^{log_23})

换底公式

对于二进制乘法，通常不需要将子问题的规模降至1。对于大多数处理器而言，16位或32位的二进制乘法都被视为一次单独的操作

通用模式

在解决规模为n的问题时，总是先递归地求解a个规模为n/b的子问题，然后再

时间内将子问题的解合并起来，其中a>0, b>1,d>=0是一些特定的整数。
此时，主定理： = aT(\lceil n/b \rceil) + O(n^d))
时间复杂度为
 =\begin{cases}O(n^d) & if ; d > log_ba \O(n^dlogn) & if ; d = log_ba \O(n^{log_ba}) & if ; d < log_ba \\end{cases})

归并排序

将该数的序列分为两部分，递归地对每一部分进行排序，最后将两个有序子序列进行合并

merge

function merge(x[1...k], y[1...l])
if k=0: return y[1...l]
if l=0: return x[1...k]
if x[1] <= y[1]:
    return x[1]+merge(x[2...k],y[1...l])
else:
    return y[1]+merge(x[1...k],y[2...l])

merge()时间复杂度为O(k+l)，即线性时间
mergesort()满足T(n) = 2T(n/2) + O(n)，根据主定理可得时间复杂度为O(nlogn)

merge()的实现通常面临两个选择：

1. 线性附加内存，花费将数据拷贝到临时数组再拷贝回来的附加工作
2. 交换位置（类似插入排序），若y半段对应元素较小，则面临将x半段对应元素至x半段末尾的元素的这一子段全体右移一位的代价

做法2可能会使归并排序退化为插入排序，因此通常选择线性附加内存

function merge(x[1...k], y[1...l])
init empty z[1...k+l]
xPos, yPos, zPos -> 1

while xPos <= k && yPose <= l:
    if x[xPos] <= y[yPos]:
        z[zPos++] = x[xPos++]
    else:
        z[zPos++] = y[yPos++]:

while xPos <= k
    z[zPos++] = x[xPos++]
while yPos <= l
    z[zPos++] = y[yPos++]
    
copy temp array z back

任一时刻只需要一个临时数组，因此该临时数组可以仅存有一个，merge()使用该临时数组的任意部分

递归版

function mergesort(a[1...n])
Input: An array of number a[1...n]
Output: A sorted version of this array

if n > 1:
    return merge(mergesort(a[1...n/2]),
                mergesort(a[n/2+1...n]))
else:
    return a

see implement: divide.MergeSortRecur

迭代版

可以发现，合并操作直到递归进入到单元素数组的层次时才真正开始，1->2->4->8...依次类推(类似自底向上)

function iterative-mergesort(a[1...n])
Input: elements a1, a2, ..., an to be sorted

Q = [] (an empty queue whose elment's type is array)
for i = 1 to n:
    inject(Q, [ai])
while |Q| > 1:
    inject(Q, merge(eject(Q), eject(Q)))
return eject(Q)

see implement: divide.MergeSortIter

扩展

在Java的泛型排序（使用Comparator）中，进行一次元素比较可能比较昂贵（因为比较可能不容易被内嵌，从而动态调度的开销可能会减慢执行的速度），但是移动元素则是省时的（因为它们是引用的赋值，而不是庞大对象的拷贝）。归并算法使用所有流行的排序算法中最少的比较次数，因此，它就是标准Java类库中泛型排序所使用的的算法。

通过两两元素之间的比较进行排序，必须要执行O(nlogn)次比较操作。
原因
通过两两元素之间的比较进行排序的算法可以通过树结构来描述，树的每个叶节点都标记一个关于原输入元素序列的排列。从树根节点到树叶节点的最长路径上的比较次数为该算法时间复杂度的最差情况。

该二叉树至少包含有n!个叶节点（排列数目），因此这棵树的宽度至少是

，因此最差情况下必须要执行O(nlogn)次比较操作，即算法复杂度为O(nlogn)

选择S中第k小元素

普通策略

1. 排序问题：对S进行排序，返回相应位置k的元素
2. 取S中k个最小数的问题：将S中前k个元素读入（某数据结构）并以递减顺序对其进行排序。接着，逐个读入剩下的元素，若该元素大于第k个元素，则忽略它；否则将其放至（某数据结构）中正确的位置，同时将第k个元素挤出。当算法终止时，位于第k个位置上的元素作为答案返回

其中某数据结构可以是数组、二叉堆、等等

分治策略

对于任意给定的数v，S中的数被分成三组：

1. ，比v小的数

2. ，与v相等的数

3. ，比v大的数
   搜索范围缩小，转而在S的三个子集中进行：
    =\begin{cases}selection(S_L, k) & if ; k<=|S_L| \v & if ; |S_L| < k <= |S_L| + |S_V| \selection(S_R, k-|S_L|-|S_V|) & if ; k > |S_L| + |S_V| \\end{cases})

在理想情况下，算法T(n) = T(n/2) + O(n)，时间复杂度为O(n)

基准v的选择see also 快速排序

分治策略的实现

由于需要多维护一个

，partition()中将S分为

,

,

三个子集不易实现。

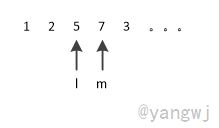
其中基准v为5，指针l左侧l为比基准v小的数，而指针m左侧为不超过基准的数。当分割时遇到比基准小的数时，需要将

和

两个子集整体向右移动一位，耗费极大时间

因此，实现时可将上述的三组放宽为：

1. ，不超过v的数

2. v
3. ，不小于v的数

显然，该变形不改变正确性

see implement: divide.FindKMin

快速傅里叶(Fourier)变换

值表示法

多项式具有如下性质

一个d次多项式被其在d+1个不同点处的取值所唯一确定
如:d=1时，即任意两点确定一条直线

该性质引出d次多项式的值表示法。

因此，对于一个d次多项式
 = a_0 + a_1x^1 + a_2x^2 + ... + a_dx^d)
有如下两种表示法（该表示法能够唯一确定该多项式）：

1. 系数表示法：多项式的系数a_0, a_1, a_2 .... a_d
2. 值表示法：A(x_0), A(x_1), A(x_2) .... A(x_d)的值

在值表示法下，对于多项式相乘问题，只要把

和

相乘，即可得到

的值，多项式相乘成为线性问题

在多项式乘法中，只要将多项式的变量x换成基数2，并留意进位，即可得到二进制乘法
多项式乘法的应用：信号处理
系数表示法和值表示法可以相互转换，系数到值的过程称为计算，值到系数的过程称为插值

求解多项式相乘（A*B=C）

• 选择

  其中

  ，因为相乘后的多项式有

  个未知数

• 计算, A(x_1), ..., A(x_{n-1}))和, B(x_1), ..., B(x_{n-1}))

• 相乘得到 = A(x_k)*B(x_k))

• 插值得到 = c_0 + c_1x + ... + c_{2d}x^{2d})

计算这步时间复杂度为

。

若对的选取有一定技巧，则可使计算过程之间产生重复步骤，从而节省算法的时间。快速

变换就是基于此将时间复杂度降为

若选择它们为正负数对，即。若以

为例，将它的奇次幂和偶次幂分离，则，

 + x(4+2x^2+10x4) = A_e(x^2) + xA_o(x^2))

则，

 = A_e(x_i^2) + x_iA_o(x_i^2))

 = A_e(x_i^2) - x_iA_o(x_i^2))

若对于正负数对的使用从递归顶层一直到到底层，那么其运算时间满足

 = 2T(n/2) + O(n))

假设我们底层选择的数选择为1，那么递归顶层选择的n个数，它们应该是，1的n次复根，即等式 的n个复数解。

复根的理解如下：

插值TODO

写在最后

• 立个Flag，TODO will be done some day。
• 渣代码，且轻喷​:worried:​。