数学学习并不是为了拥有多少数学知识,而是要在数学学习的过程中,发展孩子的思维,提高孩子的数学素养,用数学思考去分析、解决实际问题。比如破案的电视连续剧,处处不就在体现着数学的作用吗?
但如何用数学提高孩子的思维能力?我将通过多年的实践经验和引用部分家庭的培养方法总结为以下七点。
一、做出来不如讲出来,听得懂不如说得通。
>>做10道题,不如讲一道题。
孩子做完家庭作业后,家长不妨鼓励孩子开口讲解一下数学作业中的难题,我也在群里会经常发一些比较好的训练题,您也可以鼓励去想一想说一说,如果讲得好,家长还可进行小奖励,让孩子更有成就感。
原因:
做10道数学题,不如让孩子“说”明白一道题。小学数学,重在思维的训练,思维训练活了,升到初高中,数学都不会差到哪去。家长要加强孩子“说”题的训练,让孩子把智慧说出来。
孩子能开口说解题思路,是最好的思维训练模式。很多家长以为数学就是要多做题,可是有的孩子考试做错了题,但遇到同类或相似题型时,仍然一错再错。不妨让孩子把错题订正后,“说”清楚错误环节,这样孩子的思路一下子就豁然开朗了。
>>要培养质疑的习惯。
在家庭教育中,家长要经常引导孩子主动提问,学会质疑、反省,并逐步养成习惯。
在孩子放学回家后,让孩子回顾当天所学的知识:老师如何讲解的,同学是如何回答的?当孩子回答出来之后,接着追问:“为什么?”“你是怎样想的?”启发孩子讲出思维的过程并尽量让他自己作出评价。
有时,可以故意制造一些错误让孩子去发现、评价、思考。通过这样的训练,孩子会在思维上逐步形成独立见解,养成一种质疑的习惯。
二、举一反三,学会变通。
举一反三出自孔子的《论语·述而》:“举一隅,不以三隅反,则不复也。”意思是说:我举出一个墙角,你们应该要能灵活的推想到另外三个墙角,如果不能的话,我也不会再教你们了。后来,大家就把孔子说的这段话变成了“举一反三”这句成语,意思是说,学一件东西,可以灵活的思考,运用到其他相类似的东西上!
之前也常常听到家长反映,接到一些学生来信,说平时学习勤奋,请家教、上补习班,花了很多精力夯实基础知识,可考试时还是感觉反应慢、思路窄,只能就题论题,做不到举一反三,对于一些灵活性强的题目往往就束手无策。
在数学的训练中,一定要给孩子举一反三训练。一道题看似理解了,但他的思维可能比较直线,不多做几道举一反三或在此基础上变式的题,他还是转不过玩了。
举一反三其实就是“师傅领进门,学艺在自身”这句话的执行行为。
三、建立错题本,培养正确的思维习惯
每上第一次课,我所讲的课程内容都和学生的错题有关。我通常把试卷中的错题摘抄出几个典型题,作为课堂的例题再讲一遍。而学生的反应,或是像没有见过,或是对题目非常熟悉,但没有思路。
这些现象的发生,都是学生没有及时总结的原因。所以第一次课后我都建议我的学生做一个错题本,像写日记一样,记录下自己的错题和感想。
一般来说,错题分为三种类型:
第一种是特别愚蠢的错误、特别简单的错误;
第二种就是拿到题目时一点思路都没有,不知道解题该从何下手,但是一看到答案却恍然大悟;
第三种就是题目难度中等,按道理有能力做对,但是却做错了。
尤其第二种、第三种,必须放到错题本上。建立错题本的好处就是掌握了自己所犯错的类型,为防范一类错误成为习惯性的思维。
四、成为孩子探讨的伙伴,而非孩子的领导者
很多家长,在孩子学习的过程中,有意无意的说一些伤及孩子信心的话语,比如:真笨、你怎么跟你老爸一样,看看其他孩子,我怀疑你是不是亲身的,这道题都不会?快别上学了……。
我承认,思维能力是有超常的孩子,但觉对没有超笨的孩子,思维能力差,一定是外部环境与平时对孩子训练不够。
作为家长,孩子的第一任老师和生命中影响力最重要的老师,要多表扬、多鼓励,与孩子成为问题探讨的伙伴,而不是孩子的教导者和管理者。
道理越辩越明。父母要在家庭中创设一种“自由争辩交流”的氛围,当孩子学习遇到困难的时候,争辩、互相交流解决问题的方法;当孩子自己获得新的解题方法时,家长要以平和的心态,耐心地和孩子一起讨论这个解题方法的独特之处。
父母和孩子争辩解题思路,能促使孩子通过自由争辩,加深对问题的理解,拓宽思路,促使思维更灵活。这对突破固有的思维束缚、培养思维能力和品质有着良好的帮助。
五、图形推理是培养逻辑思维能力最好的工具
假是真时真亦假,真是假时假亦真;逻辑思维是在规则的确定下而进行的思维,如果联系生活就属于非常规思维。一切看似与生活毫无联系却自在法则约束规范的范围内。
逻辑推理的“瞒天过海”可谓五花八门,好似一个万花筒,百变无穷,乐趣无穷。
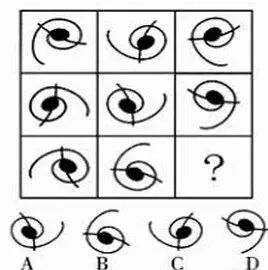
请看下面一道题,您能选出答案吗?
这道题的推理过程是:通过观察,我们唯一判断方法就是按照顺时针和逆时针来判断第一行是逆、顺、逆第二行是顺、逆、顺第三行诗逆、顺、?所以?应该是逆时针,则只有A是符合的
从这道题中,我们不仅要具备很强的观察能力,同时具备逻辑推理能力,否则,看两遍,你的大脑就跟这些图形一样:晕乎乎的。
几何图形是助其锻炼逻辑思维的好工具,经典的图形推理题总有其构思、思路、巧妙的思维;经典在于其看似变态,而实际解法却简而又简单。
因此,多训练一些图形推理题,对其逻辑思维很有帮助。
六、应巧妙利用生活中的数学提高思维能力
在家庭教育中经常有这种学以致用的机会,应该充分地加以利用。
(1)购物:低年级家长在购物中可以训练孩子的运算能力。例如拿10元钱购物,该花多少元?钱够不够?找回多少?高年级家长可以训练孩子在购物中思考哪种方法更优惠,哪种方法更合理。
(2)游戏:家长在和孩子游戏(搭积木、七巧板、下棋、摆小棒等)的同时,引导孩子用数学思考的方法去发现问题,解决游戏中的问题,提升游戏的技能与技巧。将逆推法,分类讨论法,假设法等等用于游戏当中。
(3)另外,在旅游或家庭进行投资时,都可以让孩子参与进来,进行旅游预算,运用数学思维合理安排旅游,使同样的钱发挥最大的经济效益;核计投资彩票、股票,进行银行存款、贷款等。在家庭中运用数学方法练习解决现实生活实际问题,也不失为一种训练孩子数学思维的好办法。
七、奥数是把双刃剑
奥数本是数学,之所以在数学中分出一个模块为奥数,是因为数学本身是奥妙而有趣的,一部分逻辑思维特别强或者有规律可循的题组成了奥数体系,这个体系就是为了对孩子思维和分析能力培养。
而为什么现在奥数却成了一把双刃剑,有的家长反感,有的家长支持,90%的孩子都排斥。其实很多孩子很反感奥数,其实这与孩子本身没有多大关系,而是被舆论、被有些学校老师一味的反对而造成的心里排斥。
奥秘是奥妙、有趣的,有趣的东西为什么会变得让人反感呢?
从今天起,不要在孩子面前再提奥数,它就是数学,只是在基础题上的拓展和拔高,或者说是在已有知识和能接受的范围内培养一种发散思维、逻辑思维、逆推思维等的思维训练题,它有初中的分类讨论思想和数形结合思想,引导对了,它是一门减压的学科,何为增加压力?
一个亲身的例子,我带着一个3年数学1年学的班,班里孩子学习奥数的有,没学过奥数的也有,很明显,学过奥数的孩子接受能力很强、思考能力更没法比,最后我不得不再次分层教学(其实我是很讨厌分层的),因为孩子的基础不一啊。
试问,这些学过奥数的孩子压力大,还是没有学过的压力大?
孩子心里不排斥,奥数就是以后数理化、包括语文等科目秘密武器。如果您或老师孩子给孩子树立一种“奥数没用论”,我建议趁早别说,奥数将封杀了孩子最后一点的自信心。
思维其实就是直线和曲线。一般说的感性的人就是直线思维,是顺着一条道走到黑的,不懂得返回来看看其他世界。而我们是通过多训练,让孩子的思维慢慢可以转弯、回头,让孩子在面对生活中很多问题能有独立的思考、分析和判断能力。孩子没有这项能力,永远学不好数学。
数学学习并不是为了拥有多少数学知识,而是要在数学学习的过程中,发展孩子的思维,提高孩子的数学素养,用数学思考去分析、解决实际问题。比如破案的电视连续剧,处处不就在体现着数学的作用吗?
但如何用数学提高孩子的思维能力?我将通过多年的实践经验和引用部分家庭的培养方法总结为以下七点。
一、做出来不如讲出来,听得懂不如说得通。
>>做10道题,不如讲一道题。
孩子做完家庭作业后,家长不妨鼓励孩子开口讲解一下数学作业中的难题,我也在群里会经常发一些比较好的训练题,您也可以鼓励去想一想说一说,如果讲得好,家长还可进行小奖励,让孩子更有成就感。
原因:
做10道数学题,不如让孩子“说”明白一道题。小学数学,重在思维的训练,思维训练活了,升到初高中,数学都不会差到哪去。家长要加强孩子“说”题的训练,让孩子把智慧说出来。
孩子能开口说解题思路,是最好的思维训练模式。很多家长以为数学就是要多做题,可是有的孩子考试做错了题,但遇到同类或相似题型时,仍然一错再错。不妨让孩子把错题订正后,“说”清楚错误环节,这样孩子的思路一下子就豁然开朗了。
>>要培养质疑的习惯。
在家庭教育中,家长要经常引导孩子主动提问,学会质疑、反省,并逐步养成习惯。
在孩子放学回家后,让孩子回顾当天所学的知识:老师如何讲解的,同学是如何回答的?当孩子回答出来之后,接着追问:“为什么?”“你是怎样想的?”启发孩子讲出思维的过程并尽量让他自己作出评价。
有时,可以故意制造一些错误让孩子去发现、评价、思考。通过这样的训练,孩子会在思维上逐步形成独立见解,养成一种质疑的习惯。
二、举一反三,学会变通
举一反三出自孔子的《论语·述而》:“举一隅,不以三隅反,则不复也。”意思是说:我举出一个墙角,你们应该要能灵活的推想到另外三个墙角,如果不能的话,我也不会再教你们了。后来,大家就把孔子说的这段话变成了“举一反三”这句成语,意思是说,学一件东西,可以灵活的思考,运用到其他相类似的东西上!
之前也常常听到家长反映,接到一些学生来信,说平时学习勤奋,请家教、上补习班,花了很多精力夯实基础知识,可考试时还是感觉反应慢、思路窄,只能就题论题,做不到举一反三,对于一些灵活性强的题目往往就束手无策。