Python编写动量交易策略

1. 概念介绍

动量交易策略，即Momentum Trading Strategy。在经典力学里，动量即物体质量和速度的乘积，动量一方面描述了物体的运动状态，另一方面也描述了惯性的大小。
在证券市场上，我们也可以把“证券的价格”类比成运动的物体，价格上涨时，可以说价格有着上涨的动量，价格下跌时其具有下跌的动量。这种动量可能会使上涨或下跌继续维持下去，也可能该动量会越来越小，直到使之运动状态发生改变。股票资产组合的中期收益存在延续性，即中期价格具有向某一方向连续变动的动量效应。
关于动量产生的原因，有三种说法：

1. 反应不足，即利好或利空不能一次完全消化，会持续在股价上体现。
2. 正反馈模式，即赢者恒赢，输者恒输。
3. 过度反应，即投资人对信息的高估而作出的决策。

---

2.计算动量

2.1 作差法求动量

即用今天的价格减去一段时间间隔(m期)以前的价格
$Momentu{m}_t=P_t-P_{t-m}$
Momentum_t为该股票t时期的m期动量
P_t为该股票t时期的价格
P_t-m为该股票在t-m期的价格

以平安银行(000001.SZ)日线数据为例:

# 导入相关模块
import numpy as np
import tushare as ts
import pandas as pd
import mplfinance as mpf
import matplotlib.pyplot as plt

token = 'Your token'   # 输入你的接口密匙，获取方式及相关权限见Tushare官网。
pro = ts.pro_api(token)
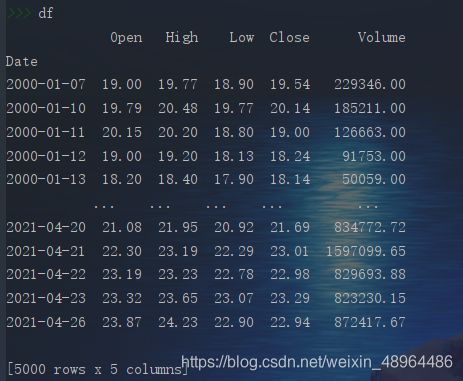
df = pro.daily(ts_code='000001.SZ')  # daily为tushare的股票数据接口。

# 将获取到的DataFrame数据进行标准化处理，转换为方便自己使用的一种规范格式。
df = df.loc[:, ['trade_date', 'open', 'high', 'low', 'close', 'vol']]
df.rename(
    columns={
     
        'trade_date': 'Date', 'open': 'Open',
        'high': 'High', 'low': 'Low',
        'close': 'Close', 'vol': 'Volume'},
    inplace=True)       # 重定义列名，方便统一规范操作。
df['Date'] = pd.to_datetime(df['Date'])  # 转换日期列的格式，便于作图
df.set_index(['Date'], inplace=True)  # 将日期列作为行索引
df = df.sort_index()  # 倒序，因为Tushare的数据是最近的交易日数据显示在DataFrame上方，倒序后方能保证作图时X轴从左到右时间序列递增。

查看一下df:

好，我们继续进行。

# 提取2020年日度收盘价
PABank =df.Close['2020']
PABank.describe()

# 假设时间跨度m为5，即求滞后5期的收盘价变量
lag5PABank = PABank.shift(5)
# 求5日动量
momentum5 = PABank - lag5PABank
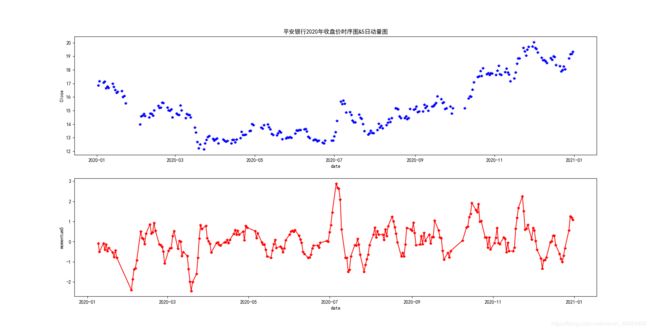
# 绘制收盘价时序图与动量曲线图
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.subplot(211)
plt.plot(PABank,'b*')
plt.xlabel('date')
plt.ylabel('Close')
plt.title('平安银行2020年收盘价时序图&5日动量图')

plt.subplot(212)
plt.plot(momentum5,'r-*')
plt.xlabel('date')
plt.ylabel('momentum5')
plt.show()

效果如图所示：

---

2.2 作除法求动量

另一种求动量的方法是作除法，使用t期的价格减去其m期以前的价格P_t-m再除以P_t-m。这种用动量变化率来表示动量的方式，将作差法得到的绝对指标转化成了一套相对指标。可以将不同的股票的股价放在一起有了一定的可比性，但是考虑到不同股票的状况不同，也要参考其本身的波动性情况。
用公式表示t时期的ROC(Rate of Change):

$RO{C}_t=\frac{P_t-P_{t-m}}{P_{t-m}}$
其中，ROC_t表示股票t时期的m期动量值。
依然以平安银行2020年收盘价为例

Momen5 = PABank/lag5PABank -1
Momen5 = Momen5.dropna()
# 然后基本同上：
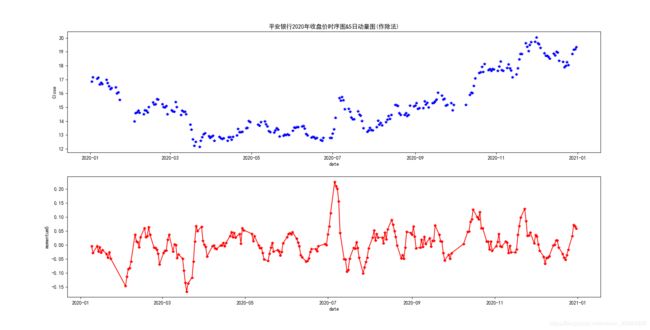
# 绘制收盘价时序图与动量曲线图
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.subplot(211)
plt.plot(PABank,'b*')
plt.xlabel('date')
plt.ylabel('Close')
plt.title('平安银行2020年收盘价时序图&5日动量图(作除法)')

plt.subplot(212)
plt.plot(Momen5,'r-*')
plt.xlabel('date')
plt.ylabel('momentum5')
plt.show()

效果如图：

3.定义求动量与作图函数

两个方法求得的动量图在图像上差别并不大。动量值一般采用作差法求得，可以编写一个求动量和作差法绘动量图的函数，以方便我们使用：

# 定义求动量的函数
def momentum(price, period):
	lagPrice = price.shift(period)
	momen = price - lagPrice
	momen = momen.dropna()
	return momen

# 定义求动量且绘时序图及动量图的函数
def momentum_plot(price, period):
	import matplotlib.pyplot as plt
	lagPrice = price.shift(period)
	momen = price - lagPrice
	momen = momen.dropna()
	
	plt.rcParams['font.sans-serif'] = ['SimHei']
	plt.rcParams['axes.unicode_minus'] = False
	plt.subplot(211)
	plt.plot(price,'b*')
	plt.xlabel('date')
	plt.ylabel('Close')
	plt.grid(True)
	plt.title('收盘价时序图(上)&{}日动量图(下)'.format(period))
	
	plt.subplot(212)
	plt.grid(True)
	plt.plot(momen,'r-*')
	plt.xlabel('date')
	plt.ylabel('Momentum')
	plt.show()
# 更多图像美化细节待你完善。

# 调用，求平安银行2020年十日动量图
momentum_plot(PABank,10)

效果如图：

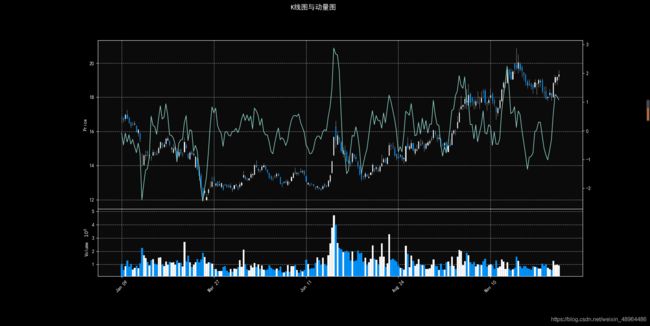
4. 绘制K线图与动量图

这次，我们选择使用万能的mplfinance库。

def candel_momen_plot(df, period):
    import matplotlib.pyplot as plt
    import mplfinance as mpf
    price = df.Close
    lagPrice = price.shift(period)
    momen = price - lagPrice
    momen = momen.dropna()
    df1 = df.loc[momen.index[0]:, :]  # 使K线图起始时间与动量图相同
    s = mpf.make_mpf_style(base_mpf_style='nightclouds', rc={
     'font.family': 'SimHei', 'axes.unicode_minus': 'False'})
    add_plot = [mpf.make_addplot(momen)]
    mpf.plot(df1, type='candle', style=s, title='K线图与动量图', addplot=add_plot, volume=True)

# 调用
candel_momen_plot(df['2020'],5)

生成图像如下(nightclouds风格)：

5. 动量交易策略的制定

四个步骤：

• 获取数据
• 确定时间跨度与计算方法
• 选择关键点
• 回测与评价。

最直觉的交易策略是动量大于0，说明股票还有上涨的能量，释放出买入信号。反之则相反。
在时间跨度m的设定上，仁者见仁智者见智，没有统一标准。
本次接下来计算将其设置为35日。

# 这次我们提取平安银行从2019年到昨天(2021-04-26)的收盘数据
Close = df['2019':'2021'].Close
momen35 = momentum(Close,35)    # 使用前边定义过的函数
signal = []   # 交易信号空列表
#  动量值为负表示卖出
# 动量值为正表示买入
for i in momen35:
	if i > 0:
		signal.append(1)
	else:
		signal.append(-1)

signal = pd.Series(signal, index=momen35.index)		

# 根据买卖点，指定买入和卖出交易，并计算收益率
tradeSig = signal.shift(1)    # 滞后一天交易
ret = Close/Close.shift(1)-1    # 计算收益率
Mom35Ret = (ret*tradeSig).dropna()  # 去空值

查看一下：

# 策略评价
# 计算胜率
win=Mom35Ret[Mom35Ret>0]
winrate = len(win)/len(Mom35Ret != 0)

查看胜率结果：

还没完，然后我们可以根据收益率与动量交易策略收益率的时序图，查看收益率分布情况：

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

plt.subplot(211)
plt.plot(ret[-len(Mom35Ret):],'b')
plt.ylabel('return')
plt.title('收益率时序图')
plt.subplot(212)
plt.plot(Mom35Ret,'r')
plt.ylabel('Mom35Ret')
plt.title('动量交易策略收益率时序图')
plt.show()

效果如下：

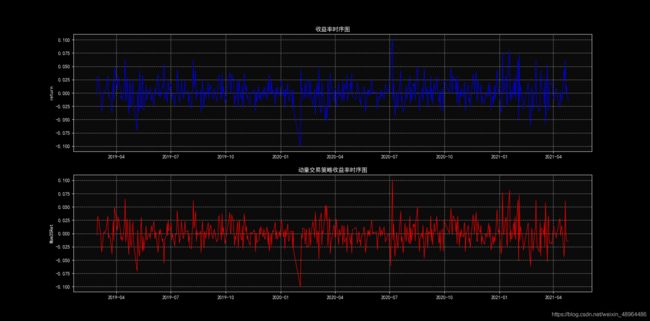
(这一点需要说明一下：在python console中，只要用mplfinance绘了一次图，在再次打开python console前，前边设定的风格会一直沿用下去了，会影响到matplotlib.pyplot。)

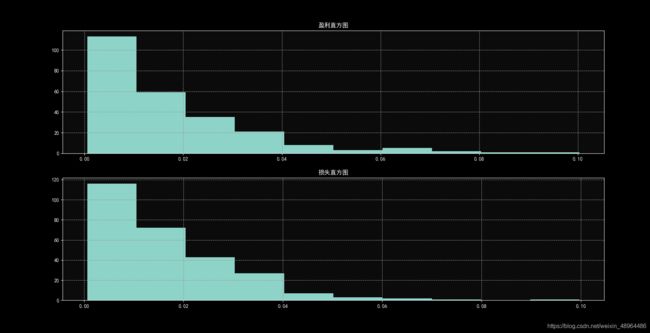
再然后，我们可以将预测成功与预测失败的收益率进行比较分析：

loss = -Mom35Ret[Mom35Ret < 0]

plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.subplot(211)
win.hist()
plt.title("盈利直方图")

plt.subplot(212)
loss.hist()
plt.title("损失直方图")

如图所示：

最后，我们计算两种收益率的平均值与分位数值：

performance = pd.DataFrame({
     "win":win.describe(),"loss":loss.describe()})

查看结果：

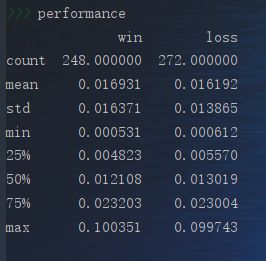
投资有风险，入市需谨慎。量化投资要结合多种策略的结论，而非单一指标。动量交易策略也只是其一。

---

路过的各路神仙大佬哥哥姐姐叔叔阿姨们，如果觉得我写得还可以的，就请点一下那个红色的关注按钮吧。以及那个灰色的大拇指，让它变成红色吧。
更多内容，敬请期待，博主会持续更新。感谢来访！