# 实现numpy_Numpy实现神经网络框架(8)——卷积神经网络基础
这篇主要讨论卷积层的实现,前面几篇讨论了一些基本概念和一些常用的层的实现,主要是围绕全连接神经网络模型开展的,而其中最为主要的线性层也叫全连接层,不过对于图像识别任务,全连接网络还是有所不足:
第一个就是参数过多,举个栗子
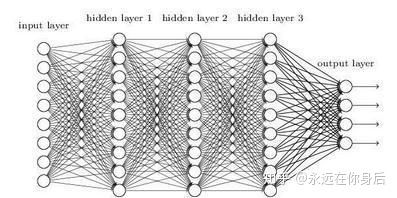
图片来自网络上图是典型的全连接网络了,而这只是个很小的网络,对比之前使用的MNIST数据集,一个样本是28x28像素的图片,展开成向量就是784个元素,如果第一个线性层神经元数目与之相当,那么光这一层的参数就是784x784,至少60万的参数,还有没算偏置(b)
如果现在有个1000x1000像素的图像,若是把该图像作为输入丢给全连接网络,展开成向量就是100万个元素,如果考虑颜色数量还要再乘3(RBG三个通道),至于接下来各层的参数,那更是无以计数,这么多参数,不但训练困难,而且容易过拟合
另一个问题就是,对于图像来说,全连接网络不能有效利用像素之间的位置信息,或者说把图像展成一维向量的时候已经破坏了这种信息,考虑下面三个向量:
a = [1 0 1 0 0 1 0 0 1 0 1 0 0 0 0 0]
b = [0 0 1 0 1 0 0 1 0 0 1 0 1 0 0 0]
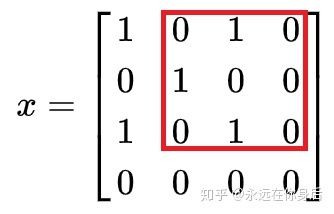
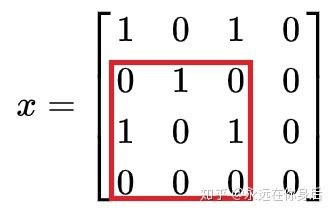
c = [0 0 0 0 0 1 0 1 0 0 1 0 0 1 0 1]粗略一看,它们似乎有些联系,值为1的元素之间距离都一样,如果是一个分类任务,那么能否将它们归为同一类?现在将它们还原成2维矩阵:
这样就看上去就很明显了,矩阵a、c都是一个‘x’,分别在左上和右下的位置,它们可以算是同一类的,而矩阵b的差异与其他两个的区别就有点大了
通过以上栗子就可以发现由于全连接网络对会图像展开,所以即使网络对于a能够很好的识别,碰到b和c这种栗子,也就不能指望它有良好的表现了;并且如果图像再大一些,或者包含多个颜色通道时,对图像的内容进行平移然后将它们展开成一个向量,差异会更加巨大
而全连接网络要解决这种由于图像内容平移所造成的差异,就需要更多的训练;但是既然a和c本质上是同一类事物,有没有方法通过一次计算将a、c和b区分开来呢?
现在假设有这么一个函数
而第二个参数
卷积函数
然后将这部分当做一个矩阵,与
这里得到3,然后换一行继续上述操作:
这里还是得到3;接下来的步骤就不用解释了,红框就这样一行行的扫过,然后点乘;根据以上的计算过程,可以知道
同理,还可以算出:
接着,再来看一个函数
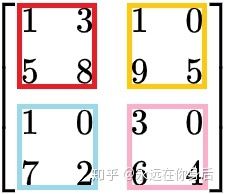
例如现在传给池化函数以下输入
并且按照步长为2计算,那么
先将
现在,将前面三个通过卷积函数计算得到的矩阵
现在,可以看到经过卷积和池化两个函数的处理,矩阵a和c的输出都是5,而b的输出是3,由是将它们区分开了
通过上述的方法,保证了网络输出对图像内容的平移不变性,而上面的卷积函数
卷积层(Convolutional layer),光看名字就知道是CNN里最核心的层了,与之前讨论过的线性层,Relu层等一样,它也有前向传播和反向传播的过程:
class Conv(Layer):
def forward(self, x):
pass
def backward(self, eta):
pass卷积神经网络的卷积层与全连接网络中的线性层对比,有几个优点:
一个参数更少,例如前面的例子中,输入数量为16(4x4),输出数量4(2x2),如果是线性层的话,需要为每个输入和输出之间设置一个权重(Weight),所以参数的数量就是64(16x4),而上面栗子中卷积层只需要使用9个参数(即卷积核的大小)
另一个是可以接受不同大小的输入,线性层一旦实例化,便只能接受固定大小的输入,而卷积层不受此限制
最后就是,线性层会将输入展成一维向量,而卷积层保留了输入元素间的位置信息
先来讨论前向传播(forward),因为forward只接受一个参数的输入,前面的卷积函数
与
卷积层的前向传播计算过程大致和前面的卷积函数中的计算过程一样,只是前面讨论的卷积计算比较基础:
二维卷积如上图中,输入和卷积核都只两个维度(分别定义为宽和高),这是二维卷积;除此之外,还有三维卷积:
三维卷积如上图所示,输入和卷积核在宽度和高度之外都多了一个维度:通道数(但是输出仍然是二维的);并且上图中输入和卷积核的通道数量一致,也就是说:卷积核的通道数必须等于输入的通道数
多通道最常见的栗子就是图片了,一个图像包含三个颜色通道,例如一个100x100大小的图片,若是用一个多维数组来存放该图片的数据,则数组大小为(100,100,3);但是卷积的输入不仅限于图片,所以也通道的数量也不止于3个,例如VGG16的卷积层最多是512个通道
更进一步的,还可以使用多个卷积核分别对输入进行卷积:
多卷积核上图中3个卷积核分别标记了不同的颜色,同时输出也变成了三维张量,其通道数与卷积核的个数相等,并且每个通道都标记了不同的颜色;也就是说:一个卷积核与输入进行卷积只得到输出的一个通道,各个卷积核之间的计算互相独立(这一点在反向传播的计算中尤其要注意)
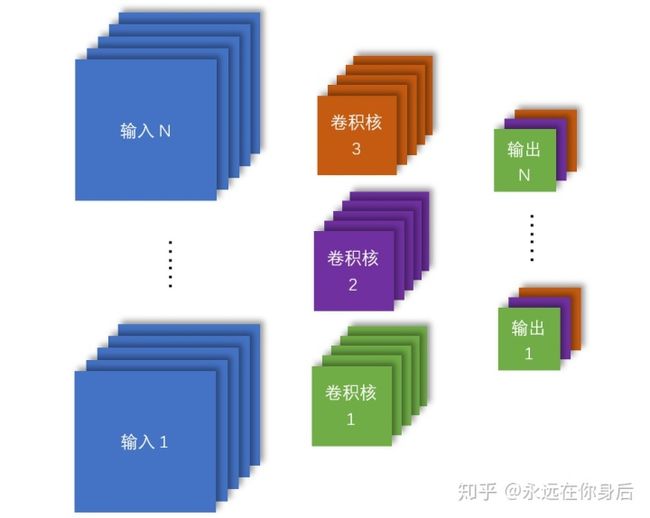
现在,输入输出都是三维的,而单个的卷积核是三维的,所有的卷积核一起可以用一个四维张量表示;又因为可以使用批量的样本进行训练,所以一整批输入可以用一个四维张量表示:
批量训练至此,卷积层的输入和卷积核都变成四维张量,并且可以和前面的情况兼容
上面的几个例子只是从大体上介绍了卷积层的前向传播,关于详细的实现和推导过程可以看:
永远在你身后:im2col方法实现卷积算法zhuanlan.zhihu.com这一篇笔记是以前写的,详细的讨论了从单个输入单通道单卷积核到批量输入多通道多卷积核的卷积计算推导过程和实现,并且已经重新改了一遍,符号约定和整体结构基本上与前几篇都是一致
除此之外,还有一篇笔记里使用了numpy自带的一个将张量分割函数(as_strided)来实现卷积算法,主要的区别是消除了im2col实现方法里的for循环,也是我的实现里使用的方法,可以对照上面一篇看
永远在你身后:卷积算法另一种高效实现,as_strided详解zhuanlan.zhihu.com卷积层的前向传播通过前面的介绍和两篇笔记的详细讨论(主要是第一篇),基本上已经说的很清楚了
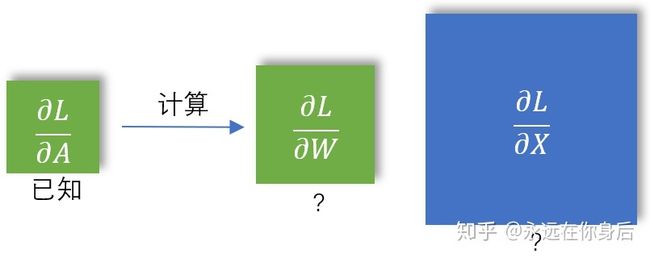
接下来介绍一下反向传播的过程,为了更好的进行讨论,先把forward中的输入、输出使用符号表示:
如上图,
那么在反向传播中,损失对于
如上图所示,其中
前向传播从基础版到最终版,反向传播也与之一一对应:
上图对应的是前面三维卷积的情况;接下来是多卷积核的情况:
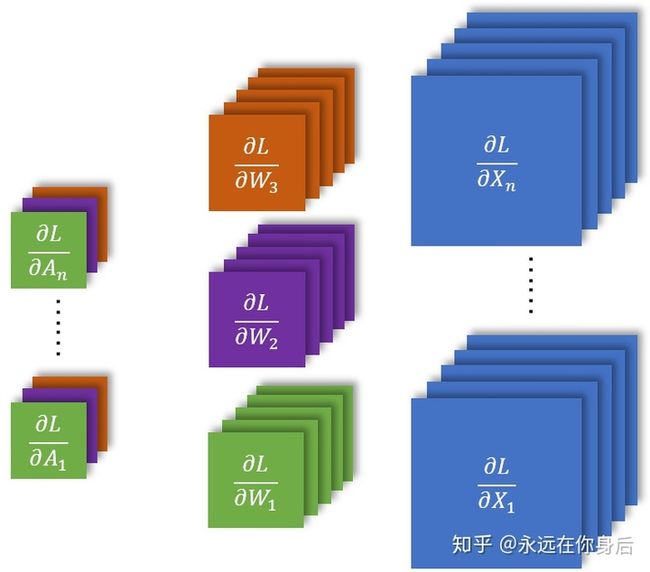
这里需要注意的是因为在前向传播的计算中,各个卷积核独立计算,所以输出的一个通道只与一个卷积核相关,那么在反向传播计算梯度是自然也是如此;最后,是批量训练时的情况:
关于卷积核的梯度(
这篇笔记也是以前总结的,但是也已经从新改过一边了,更新了一些内容,使其更加详细,也符合前面的符号约定和结构,关于卷积输入的梯度(