搜索与图论——最小生成树

1. 最小生成树定义
给定一张边带权的无向图G=(V, E)，其中V表示图中点的集合，E表示图中边的集合，n=|V|，m=|E|。由V中的全部n个顶点和E中n-1条边构成的无向连通子图被称为G的一棵生成树，其中边的权值之和最小的生成树被称为无向图G的最小生成树。

2. 最小生成树的应用
例如：要在n个城市之间铺设光缆，主要目标是要使这 n 个城市的任意两个之间都可以通信，但铺设光缆的费用很高，且各个城市之间铺设光缆的费用不同，因此另一个目标是要使铺设光缆的总费用最低。这就需要找到带权的最小生成树。

3. 最小生成树算法结构

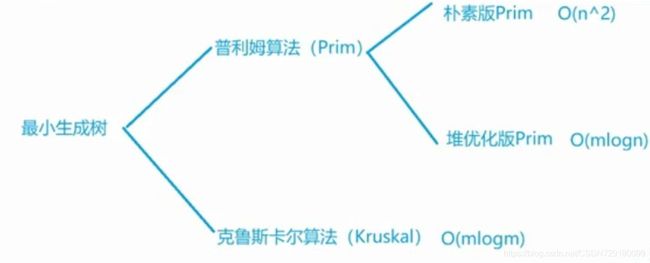
4. 朴素版Prim算法
算法思路：
1）初始化所有点到最小生成树集合的距离为无穷大
2）找到距离最小生成树集合最近的点，该点到集合的距离就是最小生成树中的一条边
3）用该点更新所有点到集合的距离
4）迭代2）3）步n次

例题：Prim算法求最小生成树——用于稠密图
给定一个n个点m条边的无向图，图中可能存在重边和自环，边权可能为负数。
求最小生成树的树边权重之和，如果最小生成树不存在则输出impossible。
给定一张边带权的无向图G=(V, E)，其中V表示图中点的集合，E表示图中边的集合n=|V|，m=|E|。
由V中的全部n个顶点和E中n-1条边构成的无向连通子图被称为G的一棵生成树，其中边的权值之和最小的生成树被称为无向图G的最小生成树。

输入格式
第一行包含两个整数n和m。
接下来m行，每行包含三个整数u，v，w，表示点u和点v之间存在一条权值为w的边。

输出格式
共一行，若存在最小生成树，则输出一个整数，表示最小生成树的树边权重之和，如果最小生成树不存在则输出impossible。

数据范围
1≤n≤500,
1≤m≤10⁵,
图中涉及边的边权的绝对值均不超过10000。

输入样例：
4 5
1 2 1
1 3 2
1 4 3
2 3 2
3 4 4
输出样例：
6

#include
#include
#include

using namespace std;

const int N = 510, INF = 0x3f3f3f3f;

int n, m;
int g[N][N], dist[N];
bool str[N];

int prim()
{
     
	memset(dist, 0x3f, sizeof(dist));

	int res = 0;	// 记录最小生成树所有边权的和
	// 循环n次，每次把一个点加入生成树的集合
	for(int i = 0; i < n; i++)
	{
     
		int t = -1; 
		// 找到距离最小生成树集合中的距离最近的点
		for(int j = 1; j <= n; j++)
		{
     
			if(!str[j] && (t == -1 || dist[j] < dist[t]))
				t = j;
		}

		if(i && dist[t] == 0x3f3f3f3f) return 0x3f3f3f3f;
		if(i) res += dist[t];	// 距离最近的点的距离一定是最小生成树中的一条边
		// 为了防止存在负的自环，要让求和在更新之前

		for(int j = 1; j <= n; j++) dist[j] = min(dist[j], g[t][j]);

		str[t] = true;
	}
	return res;
}
				
int main()
{
     
	cin >> n >> m;
	
	memset(g, 0x3f, sizeof(g));
	
	while(m--)
	{
     
		int a, b, c;
		cin >> a >> b >> c;
		g[a][b] = g[b][a] = min(g[a][b], c);
	}
	
	int t = prim();
	if(t == 0x3f3f3f3f) printf("impossible");
	else printf("%d", t);
	return 0;
}	

5. 鲁斯卡尔算法Kruskal——用于稀疏图
算法思路：
1）用结构体存储每条边的信息并根据边的权值从小到大排序
2）从小到大枚举每一条边，如果该边的两个端点不在同一个集合中（根节点是否相同）就把这两个点放到一个集合中（把一个节点赋值为另一个节点的父节点），并把这条边的权值累加。
3）判断枚举完所有边后，集合中边的数量，如果小于n-1则说明有一个点不连通，则不存在生成树

例题：Kruskal算法求最小生成树
给定一个n个点m条边的无向图，图中可能存在重边和自环，边权可能为负数。
求最小生成树的树边权重之和，如果最小生成树不存在则输出impossible。
给定一张边带权的无向图G=(V, E)，其中V表示图中点的集合，E表示图中边的集合，n=|V|，m=|E|。
由V中的全部n个顶点和E中n-1条边构成的无向连通子图被称为G的一棵生成树，其中边的权值之和最小的生成树被称为无向图G的最小生成树。

输入格式
第一行包含两个整数n和m。
接下来m行，每行包含三个整数u，v，w，表示点u和点v之间存在一条权值为w的边。

输出格式
共一行，若存在最小生成树，则输出一个整数，表示最小生成树的树边权重之和，如果最小生成树不存在则输出impossible。

数据范围
1≤n≤105,
1≤m≤2∗10⁵,
图中涉及边的边权的绝对值均不超过1000。

输入样例：
4 5
1 2 1
1 3 2
1 4 3
2 3 2
3 4 4
输出样例：
6

#include
#include
#include
#include

using namespace std;

const int N = 200010;

int n, m;
int p[N];

struct Edge
{
     
	int a, b, w;

	bool operator < (const Edge &W) const
	{
     
		return w < W.w;
	}
}edges[N];

int find(int x)
{
     
	if(p[x] != x) p[x] = find(p[x]);
	return p[x];
}

int main()
{
     
	cin >> n >> m;
			
	for(int i = 0; i < m; i++)
	{
     
		int a, b, w;
		cin >> a >> b >> w;
		edges[i] = {
     a, b, w};
	}
	
	sort(edges, edges + m);

	for(int i = 1; i <= n; i++) p[i] = i;
	
	int res = 0, cnt = 0;
	for(int i = 0; i < m; i++)
	{
     
		int a = edges[i].a, b = edges[i].b, w = edges[i].w;
	
		a = find(a), b = find(b);
		if(a != b)
		{
     
			p[a] = b;
			res += w;
			cnt ++;
		}
	}

	if(cnt < n - 1) puts("impossible");
	else printf("%d\n", res);
	
	return 0;
}