图论——最小生成树

图论——最小生成树

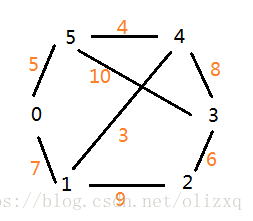
一个有 n 个结点的连通图的生成树是原图的极小连通子图，且包含原图中的所有 n 个结点，并且有保持图连通的最少的边。最小生成树可以用kruskal（克鲁斯卡尔）算法或prim（普里姆）算法求出。其实际应用比如：
我们要在n个城市中建立一个通信网络，则连通这n个城市需要布置n-1一条通信线路，这个时候我们需要考虑如何在成本最低的情况下建立这个通信网？

1、kruskal算法

（1）概览

Kruskal算法是一种用来寻找最小生成树的算法，用来解决同样问题的还有Prim算法和Boruvka算法等。三种算法都是贪婪算法的应用。和Boruvka算法不同的地方是，Kruskal算法在图中存在相同权值的边时也有效。

（2）基本思路：

先对边按权重从小到大排序，先选取权重最小的一条边，如果该边的两个节点均为不同的分量，则加入到最小生成树，否则计算下一条边，直到遍历完所有的边。

（3）图解

---

2、prim算法

（1）概览

普里姆算法（Prim算法），图论中的一种算法，可在加权连通图里搜索最小生成树。意即由此算法搜索到的边子集所构成的树中，不但包括了连通图里的所有顶点，且其所有边的权值之和亦为最小。

（2）基本思路：

所有节点分成两个group，一个为已经选取的selected_node（为list类型），一个为candidate_node，首先任取一个节点加入到selected_node，然后遍历头节点在selected_node，尾节点在candidate_node的边，选取符合这个条件的边里面权重最小的边，加入到最小生成树，选出的边的尾节点加入到selected_node，并从candidate_node删除。直到candidate_node中没有备选节点（这个循环条件要求所有节点都有边连接，即边数要大于等于节点数-1，循环开始前要加入这个条件判断，否则可能会有节点一直在candidate中，导致死循环）。

（3）图解

3、算法实现（python3）

图：

class Graph(object):
    def __init__(self, maps):
        self.maps = maps
        self.nodenum = self.get_nodenum()
        self.edgenum = self.get_edgenum()

    def get_nodenum(self):
        return len(self.maps)

    def get_edgenum(self):
        count = 0
        for i in range(self.nodenum):
            for j in range(i):
                if self.maps[i][j] > 0 and self.maps[i][j] < 9999:
                    count += 1
        return count

    def kruskal(self):
        res = []
        if self.nodenum <= 0 or self.edgenum < self.nodenum - 1:
            return res
        edge_list = []
        for i in range(self.nodenum):
            for j in range(i, self.nodenum):
                if self.maps[i][j] < 9999:
                    edge_list.append([i, j, self.maps[i][j]])  # 按[begin, end, weight]形式加入
        edge_list.sort(key=lambda a: a[2])  # 已经排好序的边集合

        group = [[i] for i in range(self.nodenum)]
        for edge in edge_list:
            for i in range(len(group)):
                if edge[0] in group[i]:
                    m = i
                if edge[1] in group[i]:
                    n = i
            if m != n:
                res.append(edge)
                group[m] = group[m] + group[n]
                group[n] = []
        return res

    def prim(self):
        res = []
        if self.nodenum <= 0 or self.edgenum < self.nodenum - 1:
            return res
        res = []
        # 选择节点
        seleted_node = [0]
        # 备选节点
        candidate_node = [i for i in range(1, self.nodenum)]

        while len(candidate_node) > 0:
            begin, end, minweight = 0, 0, 9999
            for i in seleted_node:
                for j in candidate_node:
                    if self.maps[i][j] < minweight:
                        minweight = self.maps[i][j]
                        begin = i
                        end = j
            res.append([begin, end, minweight])
            seleted_node.append(end)
            candidate_node.remove(end)
        return res


max_value = 9999
row0 = [0, 7, max_value, max_value, max_value, 5]
row1 = [7, 0, 9, max_value, 3, max_value]
row2 = [max_value, 9, 0, 6, max_value, max_value]
row3 = [max_value, max_value, 6, 0, 8, 10]
row4 = [max_value, 3, max_value, 8, 0, 4]
row5 = [5, max_value, max_value, 10, 4, 0]
maps = [row0, row1, row2, row3, row4, row5]
graph = Graph(maps)
print('邻接矩阵为\n%s' % graph.maps)
print('节点数据为%d，边数为%d\n' % (graph.nodenum, graph.edgenum))
print('------最小生成树kruskal算法------')
print(graph.kruskal())
print('------最小生成树prim算法')
print(graph.prim())

运行结果：

邻接矩阵为
[[0, 7, 9999, 9999, 9999, 5], 
[7, 0, 9, 9999, 3, 9999], 
[9999, 9, 0, 6, 9999, 9999], 
[9999, 9999, 6, 0, 8, 10], 
[9999, 3, 9999, 8, 0, 4], 
[5, 9999, 9999, 10, 4, 0]]

节点数据为6，边数为8

------最小生成树kruskal算法------
[[1, 4, 3], [4, 5, 4], [0, 5, 5], [2, 3, 6], [3, 4, 8]]
------最小生成树prim算法
[[0, 5, 5], [5, 4, 4], [4, 1, 3], [4, 3, 8], [3, 2, 6]]

参考：
https://www.cnblogs.com/biyeymyhjob/archive/2012/07/30/2615542.html
https://blog.csdn.net/mashijia986/article/details/79100925