图论——深度优先搜索

图论——深度优先搜索

什么是深度优先搜索：

深度优先搜素是对先序遍历的一种推广，和广度优先搜索不同，深度优先搜素的搜索顺序是先遍历当前节点，然后下次只先探索一个当前节点的临近节点，然后重复刚才的过程，直到达到最大深度，也就是不存在临近节点的情况，才算完成其中的一次搜索，我们这里回忆对比广度优先搜索，广度优先搜索的不同在于，可以将遍历每一层节点定义为一次探索，也就是每一次搜索中，我们都要将当前节点的全部临近节点都找出来才算完成一次搜索，而深度优先搜索是一直一个节点一个节点地向下探索临近节点，直到碰到死胡同才完成一次探索。

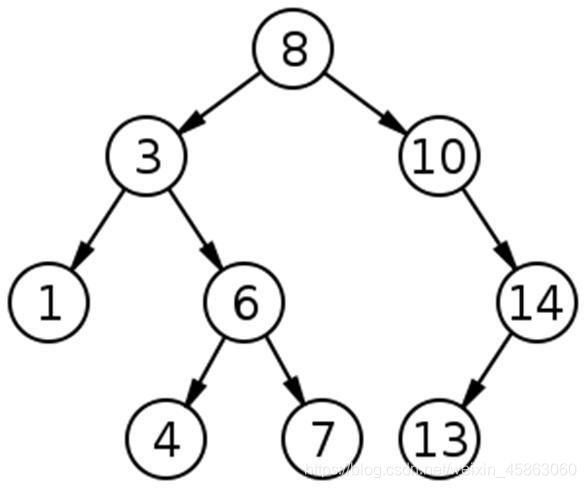
我们从百度偷来一张二叉树来表示图中某些节点的邻接关系，然后分别用深度优先搜索和广度优先搜索来表示以下对节点遍历的顺序，以区别这两种搜索方式的不同之处：
我们假设8节点也就是二叉树的根为我们探索的起始节点，也就是距离为0的节点。
我们先来说一下广度优先搜索的遍历顺序，那么也其实就相当于层序遍历这棵二叉树：8 -> 3 -> 10 -> 1 -> 6 -> 14 -> 4 -> 7 -> 13
而深度优先搜索就是先序遍历这棵二叉树：8 -> 3 -> 1 -> 6 -> 4 -> 7 -> 10 -> 14 -> 13
从树的角度来讲深度优先搜索可以被形象地描述成从根节点开始去依次遍历树地每一个分支，直到探索到每一个分支的最深处为止。

深度优先搜索的算法

假设现在有一张图，图里有很多节点，但是这是一张有向无圈图。图里有且只有一个起始节点s，和一个终点e，我们要寻找从s到e的一条路径，我们可以使用深度优先搜索来实现这样的路径查找：
无论图是否有向，我们都不能走回头路，因为一旦走回头路我们就会陷入一个圈的循环而始终无法到达某一个最大深度的终止条件。所以即便图是无方向的，我们也要注意不走回头路。这里我们为了排除这样的限制条件，从最简单的有向无圈图说起。
我们先遍历s节点，打印出s节点的数据，然后通过循环去递归地遍历s节点的全部可以到达的邻接节点，当然如果当遍历的某一个节点没有可以到达的邻接节点时，那么说明已经到达了最大深度，就直接进行返回。否则继续重复执行上面的过程。
看似简单的算法描述确实可以使我们每一次以最大深度遍历到图中的每一个可以到达的节点。

深度优先搜索的应用举例

1.全排列

我们可以使用深度优先搜索来获得一串数的全排列
假设我们给出一串没有顺序的随机整数：3 8 9 1
我们将使用DFS来得到这4个数的所有全排列

#include 
#include 
int nums[4]={
     3,8,9,1};
int book[4]={
     0};
int results[24][4];
int result[4];
int N=0;
void DFS(int step,int n)
{
     
	int i=0;
    if(step==n)
    {
     
    	//将这一次搜索到的结果加入结果集 
    	for(i=0;i<4;i++)
    	{
     
    		results[N][i]=result[i];
		} 
    	N++;
    	return;
	}
	for(i=0;i<4;i++)
	{
     
		if(book[i]==0)
		{
     
			result[step]=nums[i];
			book[i]=1;
			DFS(step+1,n);
			book[i]=0;
			result[step]=0;
		}
	}
}
main()
{
     
	DFS(0,4);
	int i,j;
	for(i=0;i<24;i++)
	{
     
		for(j=0;j<4;j++)
		{
     
			printf("%d",results[i][j]);
		}
		printf("\n");
	}
}

对上述获取全排列的DFS算法我们做以下描述：
首先在全局定义结果集数组和结果数组，用来保存每一次搜索的结果
并且额外地定义了一个很重要的book数组来记录目前结果中哪些数被用到了，以保证不会重复查找一样的数。
DFS算法使用递归的形式实现，在递归的头部，我们先判断本次搜索的步数step是否达到我们预期的步数，也就是我们期望进行全排列的数的个数，这里是4，如果step达到4的话，我们就结束本次搜索，将本次搜索到的结果result加入到结果集results中；如果没有达到预期的步数，那我们就继续进行搜索，搜索的方式是：通过循环依次遍历每一个元素，查看它是否已经在本次搜索中被使用，如果有，那么跳过它继续遍历下一个元素，如果没有，那么将它加入到本次搜索的结果中，同时在book数组中将它标记为已被搜索，然后继续调用DFS进行下一步的搜索，这里通过在DFS形参中传递step+1来表示步数的递增。值得注意的是，在一次对DFS的调用完成并返回时，我们需要在DFS调用的后面将之前进行的操作还原，这样的操作其实可以被称为回溯，这里的具体进行回溯的操作有两个，一个是将刚才book数组中标记为已经搜索的元素还原为未被搜索的状态，同时将刚才把这个元素加入结果的操作还原，当然这一步完全可以省略，因为即便不将这个元素删除也会被下一个元素覆盖。

2.图的最短路径

1.简单的走迷宫算法
假设我们通过二维数组给出一张迷宫地图，其中元素为1的位置表示有障碍不能通过，元素为0的位置表示可以通过，我们在迷宫中任意给出两个元素为0的位置分别表示起点和终点，通过DFS算法来寻找终点和起点之间的最短路径并显示这条路径和最短路径的步数。

#include 
#include 
#define N 8
int map[N][N]={
     0,0,0,1,1,0,1,1,
               1,0,1,0,0,1,1,1,
               0,0,0,0,0,0,0,0,
               1,1,1,0,1,0,1,0,
               0,0,0,0,1,0,1,1,
               1,0,1,1,1,0,1,1,
               1,0,0,0,0,0,1,0,
               1,1,1,0,1,1,1,1,   
			   };//迷宫地图 
int book[N][N]={
     0};//当前路径记录
int min_path[N][N]={
     0};//记录最短路径 
int min_step=9999999;//最小路径，初始默认为很大
void book_min_path(int [][N],int [][N]);
void DFS(int x,int y,int endx,int endy,int step) 
{
     
	if(x==endx&&y==endy)
	{
     
		if(step<min_step) 
		{
     
		 min_step=step;
		 book_min_path(book,min_path);
	    }
		return;
	}
	int direction[4][2]={
     {
     0,1},{
     0,-1},{
     1,0},{
     -1,0}};//定义方向数组，用以表示每一步的移动方向
	int i,j,k,nextx,nexty; 
	for(i=0;i<4;i++)
	{
     
		nextx=x+direction[i][0];
		nexty=y+direction[i][1];
		if(map[nextx][nexty]!=1&&book[nextx][nexty]!=1&&nextx>=0&&nexty>=0&&nextx<N&&nexty<N)// 下一位置不越界并且可通过 
		{
     
			book[nextx][nexty]=1;
			DFS(nextx,nexty,endx,endy,step+1);
			book[nextx][nexty]=0; 
		}
	}
}
book_min_path(int book[][N],int min_path[][N])//将最短路径更新 
{
     
	int i,j;
	for(i=0;i<N;i++)
	{
     
		for(j=0;j<N;j++)
		{
     
			min_path[i][j]=book[i][j];
		}
	}
}
Show_min_path()
{
     
	int i,j;
	printf("最短路径显示如下：\n");
	for(i=0;i<N;i++)
	{
     
		for(j=0;j<N;j++)
		{
     
			if(map[i][j]==1)
			{
     
				printf("@ ");
			}
			else if(min_path[i][j]==1)
			{
     
				printf("* ");
			}
			else printf("  ");
		}
		printf("\n");
	}
}

main()
{
     
	int i,j,k,startx,starty,endx,endy;
	printf("地图坐标范围为：(1,1)---(%d,%d)\n",N,N);
	printf("请输入起点：\n");
	scanf("%d %d",&startx,&starty) ;
	printf("请输入终点：\n");
	scanf("%d %d",&endx,&endy) ;
	book[startx-1][starty-1]=1;
	DFS(startx-1,starty-1,endx-1,endy-1,0);
	printf("最短路径为:  %d\n",min_step);
	Show_min_path();	
}

在这个应用中，DFS的算法思路是对每一个位置上下左右四条路径的搜索，且每次搜索都是递进连续的，除非到达终点或者碰到死胡同才开始折回，也就是回溯。
对于四个探索方向的变更，我们通过定义了一个方向数组来实现这样的功能，这是一个四行两列的数组，每一行都代表对一个方向的探索，其中每一行中的两个元素始终有一个是0，另一个为1或-1，并且每一行不相重复，这样我们通过列的循环让x和y分别去加上每一行的第一个元素和第二个元素，这样的结果是，每一次循环相加都会使x和y中的一个发生+1或者-1的变化而另一个保持不变，在图中也就代表了向某一个方向的一次移动。
探索的思路和上一个算法一样都是相同的套路，即就是如果下一个探索的目标可以被探索，那么就将其进行一些标记和相关操作，然后进行下一步的探索，并在下一步探索返回时还原这样的操作，也就是回溯操作。如果我们新探查到了一条可以从起点通向终点的路径，那么我们将这条路径所花费的步数和当前的最小步数相比较，如果这条新路径的步数更少，那么我们就更新最小步数的值，并将记录的最小路径更新呢为这条路径的位置。