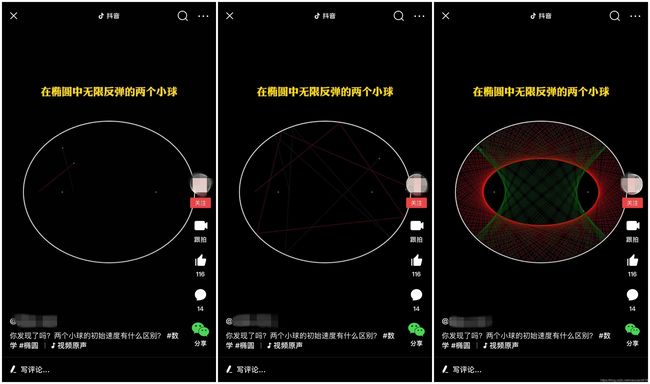
抖音同款系列——Python告诉你两个小球在椭圆内部无限反弹会产生什么效果
爬代码前先提一个问题请大家思考:
如果一个刚体小球(碰撞不形变,无能量损失)在一个同样是刚体的椭圆内部无限反弹,它的轨迹会是什么样子?(也可以考虑激光束在完美镜面椭圆内部无限反射的状态)
爱刷抖音的朋友可能看过这样一个视频,两个小球在椭圆内部无限反弹,最终的轨迹竟然是双曲线体 或 椭圆体!也不知道这个叫法对不对,大家看效果图领会吧。
配文中作者通过一个问题暗示了小球初始条件不同会导致最终轨迹不同,上文中我也专门强调了“或”字,正是与这个问题有关,这里先埋下伏笔,后面有精力的话会和大家讨论椭圆、双曲线转换的临界条件。
本文的重点是用python实现“碰撞-反弹”无限循环效果(无飞行漫游过程,有兴趣的小伙伴可以在本文基础上用pygame实现),Let’s go。
老规矩,先看效果图!!!(视频是加速播放录制的,实际速度要慢一些。)
1.做个称职的调包贼
用到numpy、sympy、matplotlib、pandas三个站点包,先写在这里了,后面不再专门import。
编程环境:python3.7.6,编辑器:Anaconda3。
# -*- coding: utf-8 -*-
"""
Created on Tue Apr 27 14:07:56 2021
@author: ck
"""
import numpy as np
import sympy #坑:scipy解多元多次方程只给出不完备解,以后弃用!
import matplotlib.pyplot as plt
from pandas.plotting import register_matplotlib_converters
from matplotlib import animation
#解决plt不显示中文
register_matplotlib_converters()
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei'] 2.数学原理
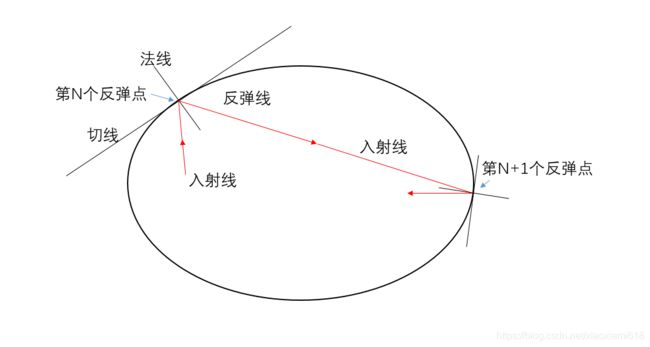
要实现“发射-反弹”无限循环,实质上就是不断计算小球每次反弹的弹射位置、方向,如下图所示
为便于大家调整参数,要强调几个重要的几何关系,对数学不感兴趣的同学也请留步一看,我保证你每个字都能看懂,绝对不用公式
对第N个反弹点有:
1)切线是反弹点(切点)处椭圆的切线
2)法线是切点处切线的垂线
3)小球入射方向与反弹方向关于法线对称(入射角=反射角),且入射轨迹与反弹轨迹交于反弹点(废话,重要的废话!)
4)第N+1个反弹点的入射线与第N次反弹线在同一条直线上,方向相同(斜率相等)
利用以上几何关系,就可以依次计算出无限“碰撞-反弹”过程中的逐个碰撞点坐标,再将这些坐标顺次连接以动画的形式实时显示出来就达到目的了。
3.初始化参数
通过上述数学原理,你会发现,要实现无限“碰撞-反弹”过程,我们还缺一个触发条件,即小球初始的发射位置和方向
所以,必须为小球指定以下几个初始化参数:
1)背景椭圆的形状参数
即文章开头提到刚体椭圆的长轴长度2a、短轴长度2b(a>b>0,椭圆定义),若焦距为2c,则由公式可得出
![]()
2)小球初始发射位置(x0,y0)
这个位置是背景椭圆上的某一点,为方便调试,我们先用位置比例参数q(0 有了x0,y0可由椭圆方程确定,由于椭圆具有上下对称的性质,一个x0对应2个y0,这里我们只用椭圆下半球方程解出一个负数y0,即将小球初始发射位置限定在下半球上(你也可以尝试从上半球发射,结果一样) 确定了发射位置,还需要确定发射方向,就可以开始“碰撞-反弹”过程了, 事实上,本步骤是要确定小球初始发射射线所在的直线(斜率k0和截距m0) 斜率k0可任意指定,m0由下式计算 在满足限制条件的前提下,初始化参数中椭圆长轴长度a、短轴长度b、位置比例参数q、初始射线斜率k0 四个参数可以任意指定,其他参数由这四个参数派生。 为便于大家上手调试代码,这里要对前文伏笔做一个简短的回应: 上述四个参数的不同组合可以生成不同形状的椭圆体、双曲线体形状,大家跟着本文敲完代码就会发现,调节参数、摸索规律才是这件事的乐趣所在!!! tip:实际操作中可以固定一组合适的a、b,只对调整位置q和发射方向k0做调节。 代码如下: 本节是按照2中的几何关系爬代码,步骤: 1)创建四个列表分别存放下一个反弹点的x、y坐标,反弹射线斜率k、截距m;显然,起始点坐标x0、y0和方向k0、m0应该分别是各自列表的第一个成员 2)联立方程,计算交点 从xs,yx,ks,ms中取出上一个反弹点的坐标、反弹线斜率、截距,构造反弹线所在直线 联立椭圆和直线方程,两组解即直线与椭圆的两个交点,分别对应第N、N+1个反弹点 3)从解集中挑出下一个反弹点坐标 由于第N个反弹点是已知的,我们要挑出哪一组解是第N+1个反弹点的坐标; 可以通过与第N个反弹点(X0,Y0)做距离判断达到目的 4)计算小球在下一个反弹点处的反弹射方向(为第N+2次反弹做准备) 切线斜率的计算用到了求导,不再展开,切线法线(垂线)、反弹线的计算用到了解析几何中向量垂直、对称的有关内容,也不再展开,大家自行推导,以下直接套用推导结果。 至此,我们完成对小球1个“碰撞-反弹-再碰撞-再反弹”动作周期的参数计算,接下来只需要将这个过程无限重复进行下去,就能得到后续所有的反弹点位置坐标和反射方向。 值得说明的是,你可以选择先用for循环限定迭代次数包裹上述代码,生成足够数量的反弹点坐标,然后再用画图工具(pygame、matplotlib、seaborn……)实现最终效果; 也可以像我一样实现实时显示,这样就需要反复调用上述代码,所以,我用while True包裹上述代码并打包成generator函数,代码如下: 这部分要使用matplotlib的animation工具,关于这个工具的用法,网上参考资料很多,不再赘述,直接贴代码: animat()函数内部只有“#双曲线”的代码,并没有椭圆,其实这里关系不大,还记得上面讲过要调整四个参数的事吗?对了!实现椭圆体和双曲线体效果在代码层面没有差别,只是参数设置不同而已。在文后贴出的完整的代码里,我会将椭圆的代码也放进来,实现椭圆体、双曲线体同时生成的效果。 看到这里,肯定会有同学产生疑问,既然是四个参数不同会导致最终的结果不同,那么产生椭圆体与双曲线体的临界条件又是什么? 关于这个问题,我没有答案,曾想用纸笔推导一下的,工作太忙,实在没有精力了,但我可以告诉大家,在临界条件下最终结果既不是椭圆体也不是双曲线,而是一个奇特的形状:一个稳定的五角星或多边形,感兴趣的话大家可以自己通过调整初始条件q0和k0试试,这两个初始值具体怎么搭配我忘了,很抱歉,如果后面想起来我会写在留言区。小伙伴们加油!!! 写到这里,我的同事袁立来博士在不停地催我走一起回家,所以,从本小节起,博文质量我不再保证,发现错误请找袁立来博士算账!!! 草草收场,跟老袁回家。 ![]()
3)小球初始发射方向
![]()
小结:
#初始化椭圆形状参数
a = 10 #长轴
b = 8 #短轴
c = (a**2-b**2)**0.5 #焦距
#初始化发射点位置
q = 0.35 #初始位置(x0,y0)横坐标在(-a,a)区间的百分比位置
x0 = -a + q * (a - (-a)) #(-a,a)
y0 = -b*np.sqrt(1 - x0**2/a**2) #初始位置出现在椭圆下半球
#初始化发射方向(初始射线斜率和截距)
k0 = -10 #初始射线斜率
m0 = y0 - k0*x0 #初始射线斜率截距
label = 'x0=%.1f,y0=%.1f,k0=%.1f)'%(x0,y0,k0)4.计算下一个反弹位置
xs = [x0,]
ys = [y0,]
ks = [k0,]
ms = [m0,]K,M,X0,Y0 = ks[-1],ms[-1],xs[-1],ys[-1]#取出上一个反弹点的坐标、反弹线斜率、截距
#联立椭圆方程和反弹线所在直线方程
ss = []
x = sympy.Symbol('x')
y = sympy.Symbol('y')
rd = sympy.solve([-b*(1 - x**2/a**2)**0.5 - y, K*x + M - y], [x, y])
if len(rd) > 0: ss.extend(rd)
ru = sympy.solve([b*(1 - x**2/a**2)**0.5 - y, K*x + M - y], [x, y])
if len(ru) > 0: ss.extend(ru)d = [((px - X0)**2 + (py - Y0)**2 , (px,py)) for px,py in ss]
d.sort(key = lambda x: x[0], reverse = True) #逆序排列
_, (x1,y1) = d[0]#距离最远的即下一个反弹点坐标
x1,y1 = float(x1),float(y1)
xs.append(x1); ys.append(y1)#计算反射点处椭圆切线的垂线斜率kk
kk = a*(a**2-x1**2)**0.5/(b*x1) if y1 > 0 else -a*(a**2-x1**2)**0.5/(b*x1)
kk = 0 if y1 == 0 else kk
# print('反射线斜率:', kk)
#计算反射线的斜率k1和截距m1
k1 = (K*kk**2 + 2*kk - K)/(2*kk*K - kk**2 + 1)
m1 = y1 - k1 * x1 ###################################计算下一个弹射点################################
xs = [x0,]
ys = [y0,]
ks = [k0,]
ms = [m0,]
def get_p1(): #双曲线
# print('start')
while True:
K,M,X0,Y0 = ks[-1],ms[-1],xs[-1],ys[-1]#出射点坐标,射线斜率、截距
# print('出射:', K, M, X0, Y0)
ss = []
x = sympy.Symbol('x')
y = sympy.Symbol('y')
rd = sympy.solve([-b*(1 - x**2/a**2)**0.5 - y, K*x + M - y], [x, y])
if len(rd) > 0: ss.extend(rd)
ru = sympy.solve([b*(1 - x**2/a**2)**0.5 - y, K*x + M - y], [x, y])
if len(ru) > 0: ss.extend(ru)
#计算反射点坐标
d = [((px - X0)**2 + (py - Y0)**2 , (px,py)) for px,py in ss]
d.sort(key = lambda x: x[0], reverse = True)
_, (x1,y1) = d[0]
x1,y1 = float(x1),float(y1)
xs.append(x1); ys.append(y1)
#计算反射点处椭圆切线的垂线斜率kk
kk = a*(a**2-x1**2)**0.5/(b*x1) if y1 > 0 else -a*(a**2-x1**2)**0.5/(b*x1)
kk = 0 if y1 == 0 else kk
# print('反射线斜率:', kk)
#计算反射线的斜率k1和截距m1
k1 = (K*kk**2 + 2*kk - K)/(2*kk*K - kk**2 + 1)
m1 = y1 - k1 * x1
ks.append(k1); ms.append(m1)
yield (xs,ys,ks,ms)5.效果实时显示
#####################################显示######################################
fig = plt.figure(figsize=(10,9),facecolor = 'black')
ax1 = fig.add_subplot(111, facecolor = 'black')
xe = np.linspace(-a, a, 1000)
yeu = b*(1-xe**2/a**2)**0.5
yed = -b*(1-xe**2/a**2)**0.5
def animat(i):#i:帧数
ax1.clear()
#双曲线
xss, yss, _, _ = next(get_p1())
ax1.plot(xss, yss, 'r', linewidth = 0.4)#轨迹
#背景椭圆
ax1.plot(xe, yeu, 'w', linewidth = 0.8)#椭圆up
ax1.plot(xe, yed, 'w', linewidth = 0.8)#椭圆down
ax1.scatter([-0.5*c,0.5*c], [0,0], s=10, c='w')#椭圆焦点
ax1.set_ylim(-a-1,a+1)
ax1.set_xlim(-a-1,a+1)
ax1.set_title(label, size = 10, c= 'w')
return ax1,
def initial():
ax1.plot(xe, yeu, 'w', linewidth = 0.8)#椭圆up
ax1.plot(xe, yed, 'w', linewidth = 0.8)#椭圆down
ax1.scatter([-c,c], [0,0], s=10,c='w')#椭圆焦点
ax1.set_ylim(-a-1,a+1)
ax1.set_xlim(-a-1,a+1)
ax1.set_title(label,size = 10, c= 'w')
return ax1,
fn = 10000
ani = animation.FuncAnimation(fig=fig,func=animat,frames=fn,init_func=initial,interval=0.001,blit=False)
plt.show()6.小讨论
7.完整代码
# -*- coding: utf-8 -*-
"""
Created on Tue Apr 27 14:07:56 2021
@author: ck
"""
import numpy as np
import sympy #坑:scipy解多元多次方程只给出不完备解,以后弃用!
import matplotlib.pyplot as plt
from pandas.plotting import register_matplotlib_converters
from matplotlib import animation
#解决plt不显示中文
register_matplotlib_converters()
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
####################################初始化椭圆参数#################################
#椭圆形状参数
a = 10 #长轴
b = 8 #短轴
c = 0.5*(a**2-b**2)**0.5
################################双曲线#########################################
#初始发射点位置
q = 0.45 #初始位置(x0,y0)横x坐标在(-a,a)区间的百分比位置
x0 = -a + q * (a - (-a)) #(-a,a)
y0 = -b*np.sqrt(1 - x0**2/a**2) #初始位置出现在椭圆下半球
#小球发射的初始方向(射线斜率和截距)
k0 = -2.4999999
m0 = y0 - k0*x0
label1 = '双曲线(x0=%.1f,y0=%.1f,k0=%.1f)'%(x0,y0,k0)
###################################计算下一个点################################
xs = [x0,]
ys = [y0,]
ks = [k0,]
ms = [m0,]
def get_p1(): #双曲线
# print('start')
while True:
K,M,X0,Y0 = ks[-1],ms[-1],xs[-1],ys[-1]#出射点坐标,射线斜率、截距
# print('出射:', K, M, X0, Y0)
ss = []
x = sympy.Symbol('x')
y = sympy.Symbol('y')
rd = sympy.solve([-b*(1 - x**2/a**2)**0.5 - y, K*x + M - y], [x, y])
if len(rd) > 0: ss.extend(rd)
ru = sympy.solve([b*(1 - x**2/a**2)**0.5 - y, K*x + M - y], [x, y])
if len(ru) > 0: ss.extend(ru)
#计算反射点坐标
d = [((px - X0)**2 + (py - Y0)**2 , (px,py)) for px,py in ss]
d.sort(key = lambda x: x[0], reverse = True)
_, (x1,y1) = d[0]
x1,y1 = float(x1),float(y1)
xs.append(x1); ys.append(y1)
#计算反射点处椭圆切线的垂线斜率kk
kk = a*(a**2-x1**2)**0.5/(b*x1) if y1 > 0 else -a*(a**2-x1**2)**0.5/(b*x1)
kk = 0 if y1 == 0 else kk
# print('反射线斜率:', kk)
#计算反射线的斜率k1和截距m1
k1 = (K*kk**2 + 2*kk - K)/(2*kk*K - kk**2 + 1)
m1 = y1 - k1 * x1
ks.append(k1); ms.append(m1)
yield (xs,ys,ks,ms)
################################椭圆#########################################
#初始点位置
q = 0.35
x10 = -a + q * (a - (-a)) #(-a,a)
y10 = -b*np.sqrt(1 - x10**2/a**2) #初始位置出现在椭圆下半球
#小球发射的初始方向(射线斜率和截距)
k10 = -1.1
m10 = y10 - k10*x10
label = label1 + '椭圆(x0=%.1f,y0=%.1f,k0=%.1f)'%(x10,y10,k10)
###################################计算下一个点################################
xs1 = [x10,]
ys1 = [y10,]
ks1 = [k10,]
ms1 = [m10,]
def get_p2(): #椭圆
# print('start')
while True:
K,M,X0,Y0 = ks1[-1],ms1[-1],xs1[-1],ys1[-1]#出射点坐标,射线斜率、截距
# print(K,M,X0,Y0)
ss = []
x = sympy.Symbol('x')
y = sympy.Symbol('y')
rd = sympy.solve([-b*(1 - x**2/a**2)**0.5 - y, K*x + M - y], [x, y])
if len(rd) > 0: ss.extend(rd)
ru = sympy.solve([b*(1 - x**2/a**2)**0.5 - y, K*x + M - y], [x, y])
if len(ru) > 0: ss.extend(ru)
#计算反射点坐标
d = [((px - X0)**2 + (py - Y0)**2 , (px,py)) for px,py in ss]
d.sort(key = lambda x: x[0], reverse = True)
_, (x1,y1) = d[0]
x1,y1 = float(x1),float(y1)
xs1.append(x1); ys1.append(y1)
#计算反射点处椭圆切线的垂线斜率kk
kk = a*(a**2-x1**2)**0.5/(b*x1) if y1 > 0 else -a*(a**2-x1**2)**0.5/(b*x1)
kk = 0 if y1 == 0 else kk
# print(kk)
#计算反射线的斜率k1和截距m1
k1 = (K*kk**2 + 2*kk - K)/(2*kk*K - kk**2 + 1)
m1 = y1 - k1 * x1
ks1.append(k1); ms1.append(m1)
yield (xs1,ys1,ks1,ms1)
#####################################显示######################################
fig = plt.figure(figsize=(10,9),facecolor = 'black')
ax1 = fig.add_subplot(111, facecolor = 'black')
xe = np.linspace(-a, a, 1000)
yeu = b*(1-xe**2/a**2)**0.5
yed = -b*(1-xe**2/a**2)**0.5
def animat(i):#i:帧数
ax1.clear()
#椭圆
xss, yss, _, _ = next(get_p2())
ax1.plot(xss, yss, 'r', linewidth = 0.4)#轨迹
#双曲线
xss, yss, _, _ = next(get_p1())
ax1.plot(xss, yss, 'g', linewidth = 0.4)#轨迹
#背景椭圆
ax1.plot(xe, yeu, 'w', linewidth = 0.8)#椭圆up
ax1.plot(xe, yed, 'w', linewidth = 0.8)#椭圆down
ax1.scatter([-c,c], [0,0], s=10, c='w')#椭圆焦点
ax1.set_ylim(-a-1,a+1)
ax1.set_xlim(-a-1,a+1)
ax1.set_title(label, size = 10, c= 'w')
return ax1,
def initial():
ax1.plot(xe, yeu, 'w', linewidth = 0.8)#椭圆up
ax1.plot(xe, yed, 'w', linewidth = 0.8)#椭圆down
ax1.scatter([-c,c], [0,0], s=10,c='w')#椭圆焦点
ax1.set_ylim(-a-1,a+1)
ax1.set_xlim(-a-1,a+1)
ax1.set_title(label,size = 10, c= 'w')
return ax1,
fn = 10000
ani = animation.FuncAnimation(fig=fig,func=animat,frames=fn,init_func=initial,interval=0.01,blit=False)
plt.show()