深入浅出强化学习编程实战——第七章笔记
深入浅出强化学习编程实战(第7章) ---策略梯度方法
一、缘由
1、概述
RL的目的是找到一种可以得到最大累计奖励的策略,其中有两大思路:
(1) 基于值函数的方法:基本思路是根据与环境交互,利用算法,计算得到状态值V和状态行为值Q,然后根据V&Q利用贪婪策略或其他策略来求出最终的Agent的策略。
(2) 基于策略的方法(直接策略搜索方法):不同于值方法,策略方法不需要计算V&Q,而是利用算法直接根据状态计算得到策略。
通俗来讲,基于值函数的方法为: ![]() ,而基于策略的方法为:
,而基于策略的方法为:![]() 。
。
2、为什么要使用基于策略的方法
(1) 直接策略搜索方法是对策略![]() 进行参数化表示,与值函数方法中对值函数进行参数化表示相比,策略参数化更简单,有更好的收敛性
进行参数化表示,与值函数方法中对值函数进行参数化表示相比,策略参数化更简单,有更好的收敛性
(2) 基于值函数的方法得到的策略是利用V&Q值加上贪婪策略(例![]() )重构得到最终策略,当要解决的问题动作空间很大或者动作集为连续集的时候,该式无法有效求解。
)重构得到最终策略,当要解决的问题动作空间很大或者动作集为连续集的时候,该式无法有效求解。
(3) 直接策略搜索方法经常采用随机策略,因为随机策略可以将探索和利用结合在一起。(直白的说,在利用随机策略的同时,由于随机策略会选择随机的动作,这本质上就是在探索,所以利用和探索耦合在了一起)
3、缺点
策略搜索方法也普遍存在一些缺点,例如:
(1) 容易收敛到局部最小值点(这是由于策略搜索方法本质上是一种优化问题)
(2) 评估单个策略时方差比较大(这是由于通常策略搜索方法的处理部分位于样本采样之后,而这里的样本是一条轨迹,所以由于策略的随机性,样本千变万化)
二、算法基本原理
1、主要思路(博主总结)
为了要找到一个好的策略,我们先随机初始化一个策略(不一定那么好),然后根据我们的目标(最大化累积奖励)来优化我们的策略的参数,即让一个初始化策略逐渐收敛到最优策略。
所以这就类似于优化参数的问题。即:![]()
书中第97的原话为:将策略进行参数化,利用梯度的方法找到最优的参数,从而得到最优的策略。
所以总的思路为:
step1:参数化一个策略![]()
step2:构建目标函数,
step3:根据目标函数的梯度来更新参数,逐渐找到最优策略
2、Step 1 初始化一个策略(策略表示)
由于我们的方法是直接搜索策略,所以策略应该是由状态直接得到的,即得到某一状态,我们通过一个函数直接得到该状态下做的动作:![]() 。
。
根据a的分布,分为了确定性策略和随机性策略,其中确定性策略表示为:![]() ,即一个状态下对应做一个动作。随机性策略表示为:s下做
,即一个状态下对应做一个动作。随机性策略表示为:s下做![]() 动作的概率为
动作的概率为![]()
如图:
(左)确定性策略表示在当前做a1动作的概率为1。(右)随机性策略表示在当前动作下做每个动作都有一定的概率。
不同的策略类型,要求我们初始化的策略函数不同。例如,对于连续动作随机性策略,我们可以利用高斯分布来拟合策略,然后逐步优化高斯分布的均值和方差。对于离散动作随机性策略,我们能可以利用softmax函数进行求解每个动作的概率,对于确定性策略的话,后面专门章节讲解。
3、Step 2 构建目标函数
众所周知,基于梯度的方法都需要找到一个目标函数,然后根据目标函数的梯度,找到最优解。RL中的策略搜索也不例外。
而RL中的一个最简单的目标就是最大化累计奖励。当认为一个策略足够好的时候,可以等价于认为这个策略可以得到更大的累计奖励。
为了忽略采样带来的偏差,在这里设定期望累计奖励为目标函数,即:
第一项为在以![]() 为参数的策略下得到本条轨迹(episode)的概率,第二项为本条轨迹的累计奖励,即:
为参数的策略下得到本条轨迹(episode)的概率,第二项为本条轨迹的累计奖励,即:
综合得到期望累计奖励函数(关于![]() 的函数)。
的函数)。
至此,可以根据目标函数进行优化![]() 了。
了。
4、Step 3 根据目标函数的梯度来更新参数,逐渐找到最优策略
目标函数为:
目标函数的梯度为:
这个最终的式子仍然是无法通过计算机来实现,所以
先将期望写成经验平均的形式:
其中 i 为第 i 条轨迹
再将式子中的P拆开:
至此:
且
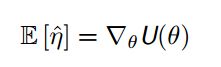 ,所以是
,所以是![]() 目标函数的梯度的无偏估计。所以我们求解梯度等价于得到
目标函数的梯度的无偏估计。所以我们求解梯度等价于得到![]()
4、总结
先产生一个策略的表达式,利用策略进行采样轨迹,并得到![]() ,则策略表达式中的参数更新公式即为:
,则策略表达式中的参数更新公式即为:
![]()
逐步迭代,找到最优的参数。











