文献阅读（十七）：So-ViT: Mind Visual Tokens for Vision Transformer

• 原始ViT：
  
• 本文创新点：
  ViT的骨干网完全由自注意力机制组成，但是性能在很大程度上取决于使用超大规模数据集进行的预训练，如果从头开始训练，它在ImageNet-1K上的性能将大大落后。本文通过利用视觉tokens，努力解决这个问题。
• 改进：具体在3.2节、3.3节、4节
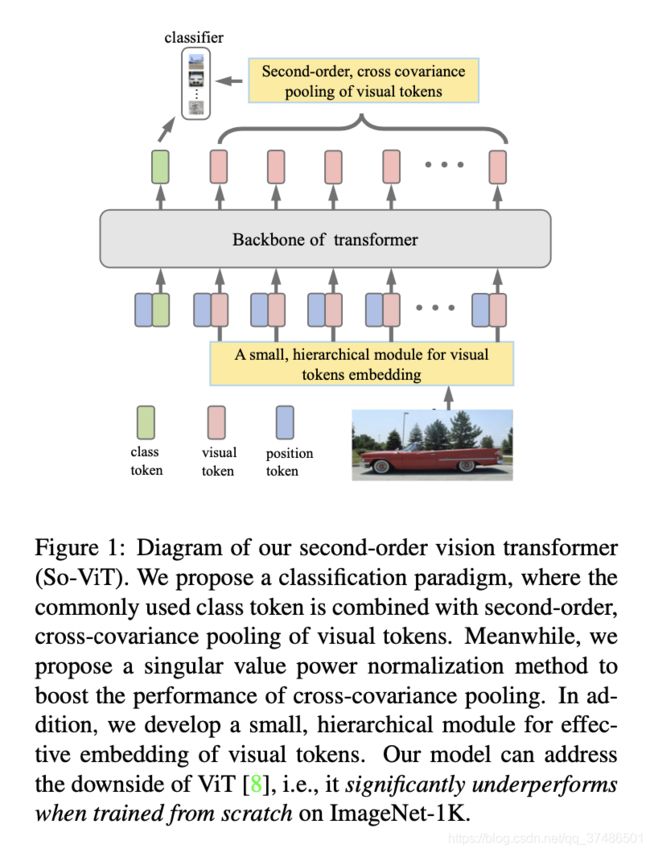
  分类head：现有的ViT利用class token，而完全忽略了高级visual token固有的丰富语义信息。——本文So-ViT：提出了一种新的分类范式，其中视觉标记的二阶交叉协方差池与class token结合在一起以进行最终分类。
  图像patches：原始的ViT采用固定大小图像patches的naive embedding，缺乏对平移等方差和局部性进行建模的能力。——本文So-ViT：开发了一种基于现成卷积的轻量级分层模块，用于visual token embedding。
  

摘要

视觉转换(ViT)体系结构以纯粹的自注意机制为核心，在视觉分类领域取得了很好的效果。然而，原始ViT的高性能很大程度上依赖于使用超大数据集进行预处理，如果从头训练，它的性能明显低于ImageNet-1K。
本文通过仔细考虑可视化标记的作用，努力解决这一问题。
首先，对于分类头，现有的ViT只利用类标记，而完全忽略了高级视觉标记中固有的丰富语义信息。因此，我们提出了一种新的分类范式，将二阶交叉协方差池化的可视标记与类标记相结合进行最终分类。同时，提出了一种快速的奇异值幂归一化方法来改进二阶池。
第二，原ViT采用固定大小的图像小块的朴素嵌入，缺乏对平移等方差和局部化的建模能力。为了缓解这一问题，我们开发了一个轻量级的、基于现有卷积的分层模块来进行视觉标记嵌入。提出的体系结构(我们称之为So-ViT)在ImageNet-1K上进行了全面的评估。
广泛的结果显示，我们的模型，当从零开始训练时，优于竞争的ViT变量，同时与最先进的CNN模型持平或更好。

1. Introduction

在过去的几年里，人们在视觉识别、目标检测和语义分割等多种计算机视觉任务上取得了显著的进展。这一进展主要是由深度神经网络的重大进步推动的[19,1]，该网络通过一堆基本构建块来学习不同级别的特征。在计算机视觉中，卷积神经网络(CNN)[36, 13, 16]是支持从视觉识别到下游任务的主要架构。尽管CNN的架构已经有了很大的发展，但基本的构建块主要依赖于卷积[20]。

与CNN截然不同的是，与CNN截然不同的是，纯粹由注意机制组成的变形结构[39]在自然语言处理(NLP)方面取得了巨大的成功。注意机制能够自然地学习cnn所面临的长期依赖和全局情境，因此引起了视觉研究者越来越多的兴趣。然而，大多数视觉任务的方法集中于开发自我注意模块，插入到cnn的骨干以提高性能。直到最近，视觉变压器(ViT)[8]，它的主干是完全由一堆变压器块构建的，在视觉识别方面取得了令人印象深刻的性能。不幸的是，在ImageNet-1K数据集上，当在超大规模的ImageNet-21K或JFT-300M数据集上进行预训练时，ViT模型能够匹配或优于最先进的cnn，但如果从头开始训练[8]，则ViT模型的性能明显低于。
有几个原因可以解释这种较差的表现。ViT的分类范式遵循NLP[39]中常用的分类范式。也就是说，对于最终的分类，ViT只利用单个类标记，而完全忽略了可视化标记。我们认为高级块的视觉信息包含丰富的语义信息，有助于分类。此外，在ViT中，视觉标记通过固定大小的图像块的简单线性投影嵌入，然后主干总是学习生成的视觉标记序列的全局关系。因此，与CNN不同的是，ViT模型不包含层次结构，缺乏对翻译等方差和局部结构[8]的学习能力。

基于以上两个考虑，我们提出了一个新的ViT架构，通过修改其分类头和视觉标记的输入嵌入。对于分类头，我们提出二阶交叉协方差池视觉标记作为全局图像表示，并与类标记相结合进行最终分类。同时，我们设计了一个轻量级的分层模块，由一个主干和一个有效嵌入视觉标记的阶段组成。然后，视觉标记嵌入到标准视觉转换器块堆栈的主干中。图1给出了所提出的模型，我们称之为二阶视觉变换(So-ViT)。

以往的研究表明，矩阵功率归一化(MPN)[40]在二阶表示中起着核心作用。然而，由于我们的池化方法产生的表示法是一般的方阵(非对称或非正定义)或非方阵，现有的MPN及其快速算法无法应用。在MPN的启发下，我们提出了奇异值幂零化(svPN)方法。svPN可以通过奇异值分解(singular value decomposition, SVD)实现，但由于奇异值分解对GPU不友好，因此计算开销较大。因此，我们进一步发展了一个近似归一化变量，这是非常快速和有效的。

我们的贡献总结如下。
•我们提出了一种二阶视觉变换架构。我们引入了一个集成了可视标记和类标记的分类范式。同时，我们开发了一个小的，分层的模块，以有效嵌入可视标记。
•我们给出了奇异值幂的归一化，一般二阶表示。此外，我们还开发了一种适用于大规模深度学习的近似归一化方法。
•我们在ImageNet-1K上进行了广泛的实验
用来验证和评估我们的方法。我们是第一批证明了当从头开始训练时，视觉转换器可以在ImageNet-1K上实现引人注目的性能的人。

2. Related works

Transformer in vision field

变压器架构[39]的巨大成功吸引了计算机视觉领域越来越多的兴趣。这种独特的注意机制在视觉识别和后续视觉任务[11]中得到了应用。关于注意机制的众多著作大致可以分为两类：
在第一类中，不同的自我注意模块被明智地设计并插入CNN的骨干以提高性能[47,41,43]。这些模块可以捕获全局上下文知识，可以缓解CNN固有的局部接受域有限的缺点。
第二类研究网络骨干网本身是否可以纯粹基于注意机制[3,48]。
最近，视觉转换器(ViT)[8]在超大规模数据集上的训练已经赶上或超过了最先进的cnn。但是，如果在ImageNet-1K上从头开始训练ViT模型，则性能会显著下降。已经提出了几种方法来克服这一限制[38,44,12]。
DeiT[38]采用知识蒸馏策略对ViT模型进行培训，引入蒸馏token向教师模型学习知识。
T2T-ViT[44]提出了一个token到token的模块，用于嵌入可视token，而不是原始ViT中使用的幼稚token化。
在TNT[12]中，提出了一种变压器中变压器块，其中外部变压器块和内部变压器块分别学习块间和块内的依赖关系。
我们的工作与这些ViT变体平行，但不同的是，我们提出了一个分类范式，集成了视觉标记和类标记的二级池，以及一种有效的视觉标记嵌入方法。

Second-order pooling in CNN

二阶池化(又称双线性池化)通常产生对称正定(SPD)矩阵作为图像表示，是一个非常活跃的课题[46,42]。在一些视觉任务中，二阶池化被证明优于一阶全局平均池化[24,40]。规范化在改善二阶表征方面起着核心作用。
双线性CNN[26]由Fisher向量法[30]驱动，引入了元素级幂标准化和l2标准化。DeepO2P[17]利用了基于协方差矩阵黎曼几何的矩阵对数归一化，但这受到了数值稳定性的困扰。矩阵幂次归一化(Matrix power normalization, MPN)[22,25]计算协方差矩阵的幂次作为图像表示，其性能明显优于同类算法。特别是Li等人[40]揭示了MPN是稳健的协方差估计，同时有效利用了协方差矩阵的几何结构。由于MPN依赖于GPU不友好的特征分解，iSQRT[21]提出了一种快速迭代计算矩阵平方根的方法，适合于GPU并行实现。最近[31]的一项研究表明，二阶池的MPN改进了损耗函数的Lipschitzness，带来了快速的网络加速和对畸变图像的鲁棒性。本文研究了一般方阵和非方阵不能应用MPN的交叉协方差矩阵的归一化问题。

3. Second-order ViT architecture

我们首先概述So-ViT架构(第3.1节)。
然后，我们描述了可视化标记的交叉协方差池，
以及如何结合类到知进行分类(第3.2节)。
最后，我们介绍了可视化标记嵌入方法(第3.3节)。

3.1. Architecture overview

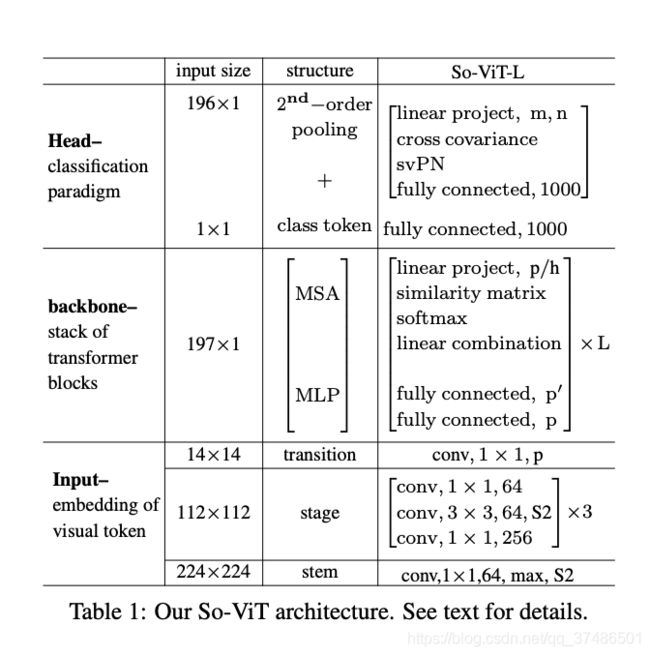
表1中给出了我们的二阶ViT (So-ViT)体系结构。在给定输入图像的基础上，设计了一个轻量级的分层结构模块，实现了视觉标记的嵌入。该模块是一个基于卷积的小型网络，由一个主干和一个级组成。从嵌入模块的卷积特征被重塑为一个向量序列作为视觉标记。
和[8]一样，我们在可视标记序列前添加一个可学习的类标记class token，然后添加位置嵌入以保留位置信息position embeddings。token sequence通过堆叠标准变压器块[8]送入主干。每个transformer block 由多头自注意(MSA)和多层感知器(MLP)组成。每个变压器块前后分别采用Layer normalization and shortcut connection。在每个SA中，将输入特征分别线性投影到称为查询、键和值的特征上，然后计算查询和键之间的相似度矩阵，最后通过将这些值与相似度矩阵相乘(在softmax之后)来计算值的线性组合。MLP包含两个完全连接(FC)层，在第一个FC之后有一个GELU非线性。通过主干，标记维数、头数和隐藏层维数(分别用p、h和p’表示)保持不变。
我们结合 visual tokens and class token进行分类。我们通过两个独立的线性投影将视觉标记映射到低维m和n的特征上。然后我们对特征的两个分支进行交叉协方差池，产生二阶表示。通过svPN对可视化标记进行归一化后，将其与类标记的表示相结合，提供给最终的softmax分类器。

3.2. Fusing class and visual tokens for classification 融合类和可视标记进行分类

变压器模型的传统分类范式完全依赖类标记，完全抛弃了视觉标记[8,39]。高级视觉符号包含丰富的图像语义知识，是类符号的补充。因此，我们提出了视觉tokens的二阶池，与类tokens集成用于分类。
设Z∈Rp×N是一个矩阵，其中每一列是一个视觉标记的p维特征。我们对特征矩阵Z分别进行两个线性投影，得到X = W1Z和Y = W2Z，其中W1∈Rm×p和W2∈Rn×p是可学习权矩阵。在不失一般性的前提下，我们假设X和Y都以零为中心，且m≥n。我们计算X和Y之间的交叉协方差矩阵，即XYT，然后奇异值幂零化作为二阶全局图像表示：
svPN（XY协方差矩阵）

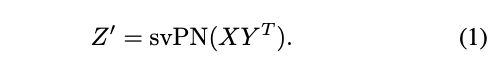
注意XYT可以是一般的方阵(非对称或正定)或非方阵。正如[40]所指出的，规范化对全局二阶池起着重要作用。然而，矩阵功率归一化及其快速版本[40]只能用于SPD矩阵。我们提出了交叉协方差矩阵的奇异值幂归一化(svPN)。我们将svPN的动机和方法的细节推迟到下一节。
备注1。我们的二级表征XY T不同于自我注意(SA)机制。一个SA的输出形式可以是(XY T)W3Z，基本上是一阶表示，因为它是输入Z的线性组合，其中线性组合的系数由相似矩阵XT Y计算。这里W3是一个可学习权矩阵。
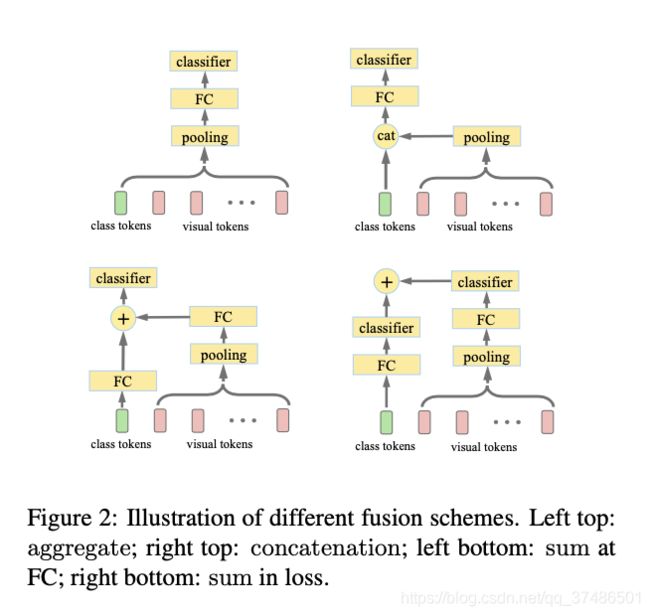
我们介绍了类tokens与视觉tokens相结合的几种融合方案，即聚合、求和、拼接，如图2所示。我们建议为可视化标记使用交叉协方差池。我们认为，一级全局平均池也可以使用[23,36,13]。
对于聚合方案，我们在最后一个变压器块(tranL)之后为所有令牌执行池，然后连续连接到FC和softmax分类器。
对于拼接方案，我们在tranL之后，将类标记和视觉标记的池化结果进行级联，并将级联后的表示提供给FC和softmax分类器。
对于求和方案，我们有两个独立的分支:一个分支是常用的类令牌，后面跟着FC，而另一个分支在汇集可视令牌之后，连接到一个单独的FC。两个fc的输出可以添加到一个softmax分类器中。或者，我们可以将每个FC连接到一个独立的softmax分类器，然后将这两个分类损失相加。

3.3. Embedding of visual tokens嵌入可视标记

原有的ViT缺乏翻译等方差和局域性的归纳偏差，而依靠超大的训练数据来克服这一限制[8]。一个自然的替代方案是将CNN和transformer结合起来的混合模型。在[8]中，ResNet-50第4阶段的卷积特征被反馈到变压器模型中，使得混合模型很重而获得很少。我们的理念是不同的:我们的想法是一个用于嵌入可视tokens的小层次模块，而主干仍然依赖于transformers块。
我们提出了一个轻量级的分层模块来实现视觉标记的嵌入，而不是在[8]中通过固定大小的补丁的线性投影来实现的简单方法。我们的模块非常简单，由一个干stem和一个阶段stage组成。
该stem由3×3卷积(conv)与64个滤波器，随后的最大池化stride 2 (S2)。
后续stage阶段包含3个剩余瓶颈[13]的堆栈。每个瓶颈的中间3×3 conv的下采样步长为2。
为了兼容后续变压器块的尺寸，我们利用了一个带有p通道的1×1 conv过渡层。在每个卷积层之后依次是BN层和ReLU层。对于H × W像素的输入图像，我们的标记嵌入的输出是空间大小为H/8 × W/8的特征映射，有p个通道，其中p是变压器块的维数。通过将空间维度展平，我们得到了一个N = HW/64个p维视觉标记序列。
我们模块中的阶段是基于ResNet块的。无论如何，我们的选择是非常灵活的:我们也可以堆叠Inception块[37]，DenseNet块[16]，或者非本地块[41]。我们的实验(5.1节)表明，这些不同的选择表现良好，都优于T2T[44]的视觉标记嵌入竞争方法。这表明我们基于卷积的嵌入思想很重要，而不是特定的卷积块。

4. Normalization of cross-covariance matrix交叉协方差矩阵的标准化

我们首先描述交叉协方差矩阵的奇异值幂归一化svPN(第4.1节)。接下来，我们介绍一种高效快速的近似svPN(4.2节)。

4.1. Singular value power normalization奇异值功率归一化

我们的方法是基于MPN[40]，这是一种对协方差矩阵XXT进行归一化的有效方法。它由协方差矩阵的特征向量对应的特征值的计算能力构成。主成分分析的最大方差公式[2，第12章]指出，将随机样本连续投影到主成分的不相关方向上，可以依次得到从方差最大到方差最小的结果。由于主成分/方差对应于协方差矩阵的特征向量/特征值，所以MPN可以统计上解释为根据主成分特征方向缩小方差。进一步，我们提出了交叉协方差矩阵XYT的奇异值归一化。
我们把X和Y分别看作随机向量X∈Rm和Y∈Rn的N个样本组成的两个矩阵。设u∈Rm, v∈Rn为两个单位向量，即:∥u∥=∥v∥= 1。我们知道R(Q,u,v) = uTXYTv是x在u上的投影和y在v上的投影的协方差，其中Q = XYT。对目标maxu,v，∥u∥=∥v∥=1 R(Q, u,v) = uT XY T v的解u1和v1是对应于最大值λ1 = R(Q, u1, v1)的左、右奇异向量。给定uk和vk, k≥1，在uTui =0andvTvi =0fori

4.2. Approximate, fast singular value power nor- malization近似，快速奇异值幂化

基于机器学习[10]中广泛使用的低秩假设，我们只需估计几个最大奇异值就可以有效地实现近似归一化。我们利用[34]中引入的迭代法，按降序连续估计奇异值。给定初始向量v(0)，迭代过程采用如下形式:

其中上标表示迭代次数。经过多次迭代，我们得到了近似的最大奇异值σˆ1 =∥QT u(j+1)∥和相应的左、右奇异向量uˆ1 = u(j+1)， vˆ1 = v(j+1)，其中ˆ表示它们是近似的值。假设我们有第k个最大奇异值，我们压缩矩阵Q得到

合理的做法是，我们将第1个奇异值缩小到(r−1)个奇异值，与相应的奇异向量对齐，同时使用第r个最大奇异值来缩小剩下的奇异值。

5. Experiments

我们首先评估了提议的So-ViT架构(第5.1节)，
然后进行了奇异值功率归一化的奇异值研究(第5.2节)。
然后我们与T2T-ViT[44]进行比较，这与我们的方法密切相关(5.3节)。
最后，我们比较了目前最先进的ViT变体和CNN模型(5.4节)。

我们的实验是在ImageNet-1K基准[6]上进行的，该基准[6]包含128万张训练图像和5万张验证图像。
我们的实现：
基于PyTorch框架，
模型使用8个NVIDIA 2080Ti gpu进行训练。
我们从零开始训练So-ViT模特。
我们采用标准尺度、颜色和翻转抖动进行数据增强[18,13]。
在[44]之后，我们还采用了一些常用的数据增强技术，包括mixup[14]、randAugment[5]、cutmix[45]，以及值为0.1[36]的标签平滑。
我们使用AdamW[28]算法进行网络优化，
batch为512，
权值衰减为0.05。
迭代从初始学习速率1e-6开始，增加到5e-4(重复，1e-3)，在14和19模型的三个预热期(重复，7和10)变压器块。
我们使用最终学习率为1e- 5[27]的余弦退火算法。
我们使用310个训练epoch，因为变压器模型需要更多的迭代[8,44,12]。为了便于5.1和5.2节中广泛的烧蚀分析，我们使用了包含7个transformer blocks(即So- vita -7)的浅网，图像分辨率为112×112。为了与最先进的模型进行比较，在5.3和5.4节中，我们采用了传统的图像分辨率224×224。
我们设计了一系列具有不同数量的变压器块L的模型，即So-ViT-7/10/14/19，其中p =256/256/384/448, h = 4/4/6/7，其中对于前两个模型p ’ = 2p，对于后两个模型p ’ = 3p。

5.1. Evaluation of the So-ViT architecture

本节评估所提出的视觉token嵌入方法、将视觉token与类token集成起来的分类范式。

可视化标记嵌入模块
我们的嵌入模块如表1底部所示，由一个3 × 3 conv的stem和一个由3个残块组成的stage组成。stage的设计也可以基于Inception, DenseNet或Non-local块。由于篇幅有限，有关嵌入变体的细节见附录。

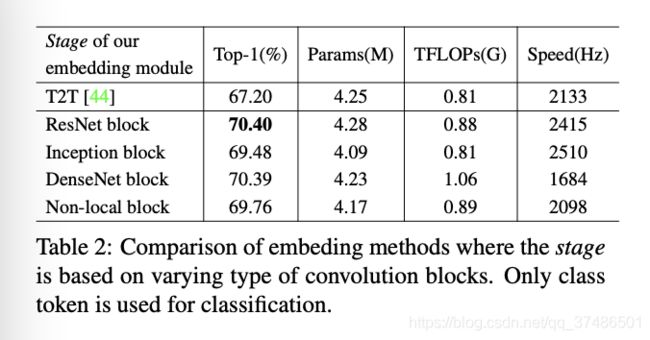
表2比较了不同嵌入模块和T2T模块[44]。我们提到T2T模块是一个强基线，其中软分裂操作被引入到变压器块堆栈之前的变压器块中，以学习visual标记的局部结构。值得注意的是，所有基于卷积的嵌入模块的性能比T2T模块高出约2% ~ 3%。结果表明，基于卷积的嵌入方法是非常有效的。这也暗示了自动设计更高级的嵌入方法的潜力(例如，通过神经结构搜索[9])。

分类头的融合方案

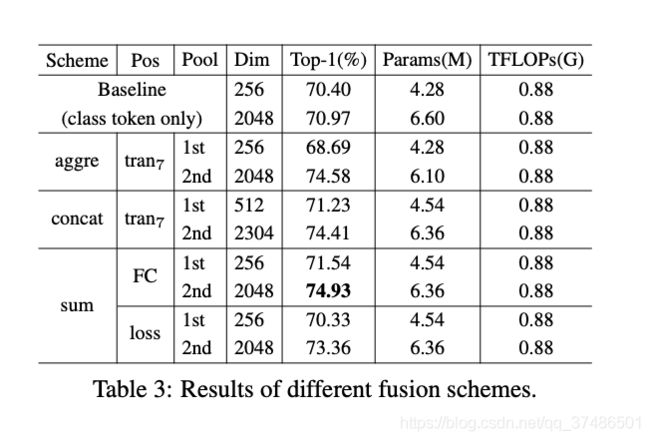
不同融合方法的比较见表3。我们首先注意到，所有使用二阶池的融合方案都比基线的性能好约2 ~ 4%，参数略有增加，但不影响TFLOPs;
sum (FC, 2)方案效果最好，准确率比基线高4.5%。
对于一阶池融合方案，concat和sum (FC)方案优于基线方案，其他两种方案均低于基线方案。由于基线表示的维数(256-D)小于融合方法的维数，为了便于比较，我们在基线上增加了一个额外的线性投影，将类标记的维数增加到2048，称为基线+。
我们注意到基线+比基线略有改善，但仍明显落后于最佳融合方法(70.97 vs. 74.93)。
这表明，所提方法的性能提高主要是由于我们的分类范式(即融合方案)，而不是简单地增加维度。
从上面的分析，我们有两个观察：
(1)视觉标记与类标记相结合的分类效果明显优于单类标记，表明了所提出的分类范式的有效性。(2)与一阶池相比，二阶池获得了较大的收益，说明所提出的交叉协方差池对视觉标记是非常有效的表示。

5.2. Evaluation of svPN for second-order pooling

在本节中，我们将评估精确的标准化(即svPN)和近似的标准化(即s^vPN)。
然后，我们比较相似矩阵和交叉协方差矩阵。
然后，我们评估交叉协方差矩阵大小对绩效的影响。
最后我们比较了不同的归一化方法。
精确归一化和近似归一化
我们的归一化svPN可以通过计算所有奇异值/向量的奇异值分解(SVD)精确实现。近似方法s^vPN
使用简单的迭代算法来逼近少数奇异值/向量。
对于svPN，表4a上半部分显示了指数α (Eq. 2)的效果，其中α = 0.5的精度最高。然而，通过SVD的svPN在计算上非常昂贵，仅以110赫兹运行。在表4a的下部分，设置α = 0.5，我们评估奇异值的数量(#sv)和迭代次数(#iter)对s^vPN (Eq. 6)
的影响。我们注意到总体上近似归一化略低于精确归一化。当只使用最大奇异值时，迭代次数的增加带来的收益并不显著。值得一提的是，在光谱归一化[29]中也观察到类似的现象，在权值归一化中只使用一次迭代来估计最大的奇异值。当我们使用两个或三个最大的奇异值时，我们观察到性能下降。我们认为原因是，后续奇异值/向量的估计受到了前一个不准确的严重影响。本文采用单最大特征值的s^vPN对二阶池进行一次迭代归一化。
交叉协方差矩阵与相似矩阵
如第3.2节所述，我们使用视觉标记的交叉协方差矩阵XY T作为最终的图像表示。另外，也可以使用相似矩阵xty。这里我们比较表4b中的两种不同表示。可以看出，相似度矩阵的正确率比交叉协方差矩阵低约4.9%。需要注意的是，相似度矩阵是空间位置相关的，这意味着平移图像中的物体会导致不同的表示方式，不利于分类。相反，交叉协方差矩阵是一个稳健的，位置不变的表示，即，任何视觉标记的排列产生相同的交叉协方差矩阵。

交叉协方差矩阵的维数
协方差矩阵的维数为m × n，其中m和n为两个线性投影的维数，如3.2节所述。表4c显示了交叉协方差矩阵的维数(Dim)对性能的影响。我们可以看到，当尺寸变大时，精度不断增加。当Dim=8K时，准确率比只使用class token的基线(70.4%，表3)高7.6%。当Dim为512时，准确率仍然比基线高2.8%。请注意，较高的Dim会导致更大的参数数，但计算量的增加非常小。为了性能参数的折衷，我们选择Dim=2K，除非另有指定。

比较不同的归一化方法
我们将其与基于元素的功率归一化(EPN)进行比较，我们调整了功率的值，得到的值为1/2作为最佳超参数。我们还比较了层归一化(LN)和一种简单的缩放方法，即除以√N，其中N是可视标记的数量。我们没有与MPN(或其更快的视觉iSQRT-COV)进行比较，因为交叉协方差池产生的一般方阵或非方阵是MPN不能应用的。对比结果见表4d。我们可以看到，所有的规范化方法都比没有规范化的基线有所改善，这说明了规范化对于二级池的重要性。在所有归一化方法中，我们的svPN表现最好，top-1的精度比次优方法高0.5%，比基线提高约1.1%。

5.3. Comparison with T2T-ViT

与我们的方法类似，T2T-ViT提出了一个T2T模块来更好地嵌入令牌，而不是原始ViT中的朴素嵌入方法。因此，本节将与这个ViT变体进行比较，结果如表5所示。

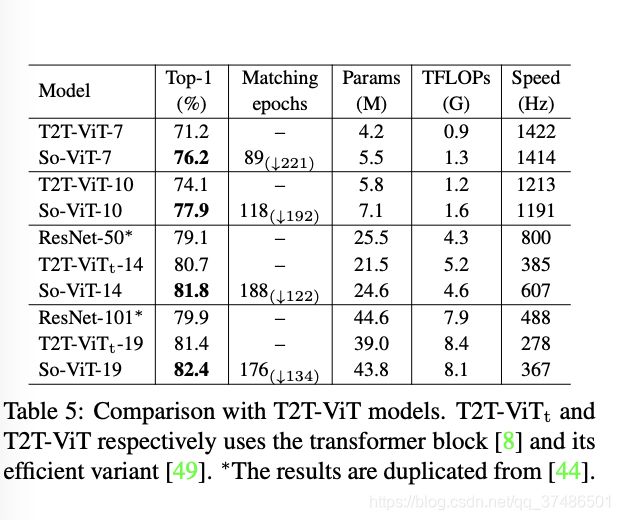
由于ResNet-50/101与so -vit-14/19的计算具有可比性，我们也列出了他们的结果以供参考。我们首先注意到So-ViT和T2T-ViT模型都明显优于ResNet模型。这说明变压器模型具有较强的表示学习能力。此外，当使用相同数量的变压器块时，我们的So-ViT始终优于T2T-ViT 1% ~ 5%。
接下来，我们比较它们的收敛性和速度。总的来说，我们的模型比T2T-ViT的收敛速度快，因为我们的So-ViT的性能可以与训练了310个epochs的T2T-ViT相媲美。例如，T2T- ViT-14在310epochs的情况下达到80.7%的精度，而我们的模型只需要188epochs就可以获得相同的精度。特别是对于较浅的模型，So-ViT收敛速度更快，例如，具有89个时点的So-ViT-7可以达到具有310个时点的T2T-ViT-7的性能。对于7/10变压器块的较浅型号，我们的So-ViT具有与T2T-ViT相当的速度，T2T-ViT使用一个高效的变压器块[49]。对于深度为14/17的车型，我们的So-ViT比T2T-ViT快1.3倍。

5.4. Comparison with state of the art

最后，我们比较了依赖于ViT或CNN的最先进的模型。对于ViT变体，我们比较T2T-ViT [44]， DeiT[38]和TNT[12]。在表6的上半部分，我们比较了针对移动应用程序的精简模式。

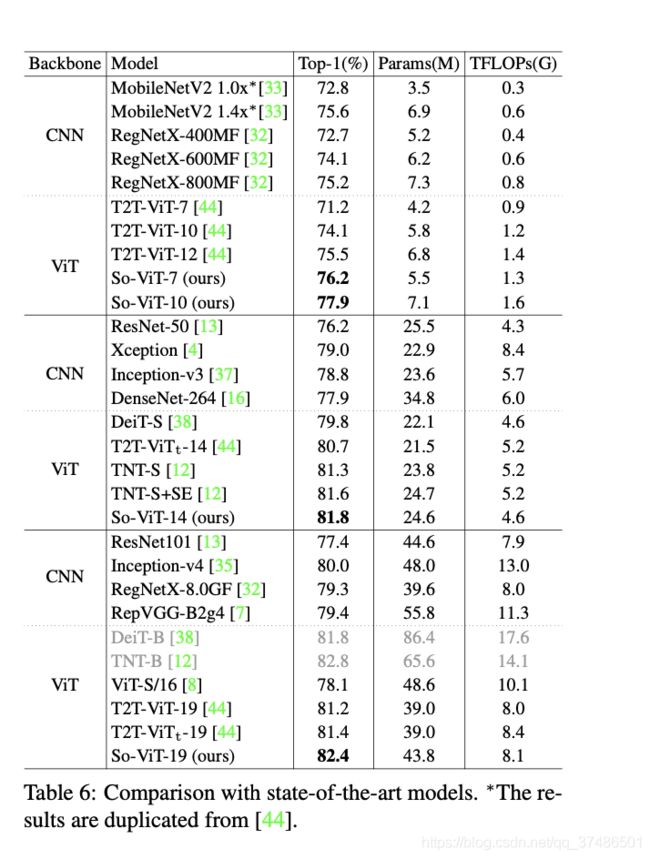
可以看出So-ViT-7的准确率比T2T-ViT- 10高2.1%，So-ViT-10与T2T-ViT- 12的准确率差距约为2.4%。表6的中间部分比较了与ResNet- 50具有可比性计算的模型。可以看出，我们的so-vit-14比DeiT-S、t2t -vit-14t和TNT-S分别高出约2.0%、1.1%和0.5%。通过结合SE块[15]，TNT-S的精度有所提高，但仍低于我们的精度。
如表6底部所示，我们的so-vit-19比t2t -vit-19的表现好1.0%;TNT-B的精度比我们的高，但它的参数和TFLOPs要大得多。
最后，我们注意到，无论是针对移动环境的精简网络，还是针对高性能的复杂、更深层次的模型，所提出的So-ViT模型的性能都与最先进的CNN模型不相上下或更好。

6. Conclusion

提出了一种用于图像分类的二阶视觉变换(So-ViT)模型。对于网络头，我们提出将视觉tokens的交叉协方差池与类令牌集成到分类器。据我们所知，这是首次尝试利用转换器体系结构中的高级可视特性进行最终分类。对于网络输入，我们设计了一个基于现有卷积的有效视觉标记嵌入的小层次模块。大量实验表明，与目前最先进的ViT模型和CNN模型相比，我们的So-ViT模型具有很强的竞争力。我们的视觉标记嵌入思想的有效性表明，通过NAS[9]自动寻找嵌入模块是很有前途的。未来，我们有兴趣研究我们的So-ViT将如何执行NLP[39]的任务。