机器学习-数据科学库(HM)-numpy部分
numpy是python中做科学计算的基础库,重在数值计算,也是大部分python科学计算基础库,多用于大型、多维数组上执行数值运算。类似于matlab的数据方法。这里就不再详细解释,可以去查看一下我的matlab相关文章。
创建数组(矩阵)
创建一维数组
两种方式:
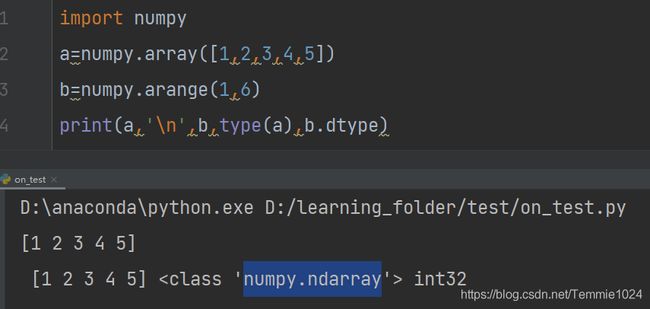
import numpy
a=numpy.array([1,2,3,4,5])
b=numpy.arange(1,6)
注意:虽然在print时,样子与列表很像,但它的类型是numpy.ndarray
数据类型,设置与修改
比也可能注意到了最后的b.dtype,.dtype用来打印数组中的数据类型。
数据类型包含:

你可以在定义数组的时候直接指定数据类型:
import numpy
a=numpy.array([1,2,3,4,5],dtype='int8')
print(a,a.dtype)
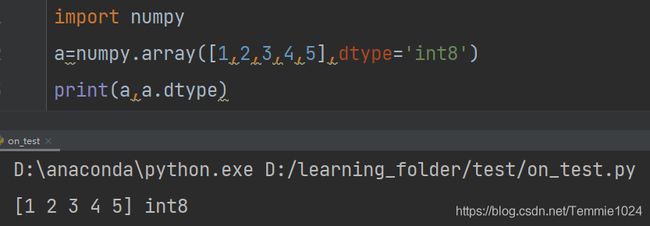
也可以在定义后修改数据类型:
是强制转换。
注意,不是真正的修改,原数据实际上是没动的
源代码是这样说的:

import numpy
a=numpy.array([1,2,3,4,5])
print(a,a.dtype)
b=a.astype(dtype='int64')
print(b,b.dtype)
修改小数位数
import random
random.random()#用于产生0-1之间的随机数
round(要改变的数组,保留小数点后位数)
import numpy
import random
a=numpy.array([random.random() for i in range(10)])
print(a)
b=numpy.round(a,2)
print(b)
多维数组
类似于列表套列表,详细的写法看代码即可。
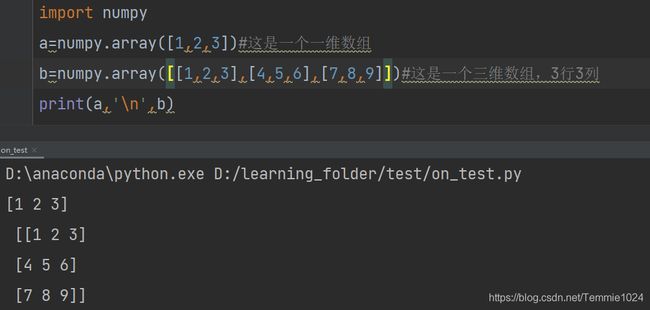
import numpy
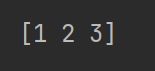
a=numpy.array([1,2,3])#这是一个一维数组
b=numpy.array([[1,2,3],[4,5,6],[7,8,9]])#这是一个三维数组,3行3列
print(a,'\n',b)
查看数组形状shape
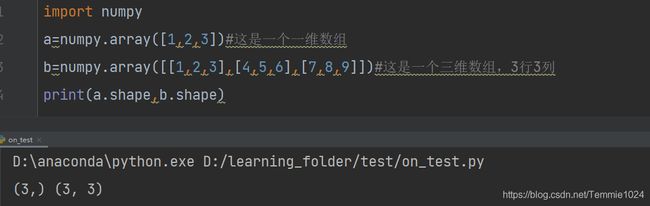
import numpy
a=numpy.array([1,2,3])#这是一个一维数组
b=numpy.array([[1,2,3],[4,5,6],[7,8,9]])#这是一个三维数组,3行3列
print(a.shape,b.shape)
修改数组形状为a行b列reshape((a,b))
对于高维数据一样,但是很难理解高于三维的内容,所以,这里只提一下二维和三维数组。
二维:
import numpy
a1=[1,2,3];a2=[4,5,6]
a=[a1,a2]
a_array=numpy.array(a);print('a_array:','\n',a_array,'\n',a_array.shape)
bb1=[1,2,3];bb2=[3,4,5];bb3=[5,6,7];bb4=[7,8,9]
b1=[bb1,bb2];b2=[bb3,bb4]
b=[b1,b2]
b_array=numpy.array(b);print('b_array:','\n',b_array,'\n',b_array.shape)
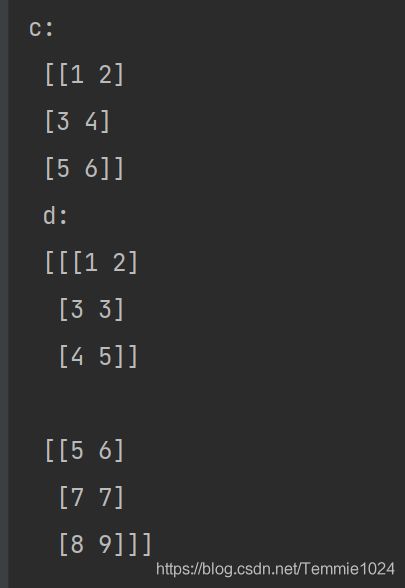
c=a_array.reshape(3,2)
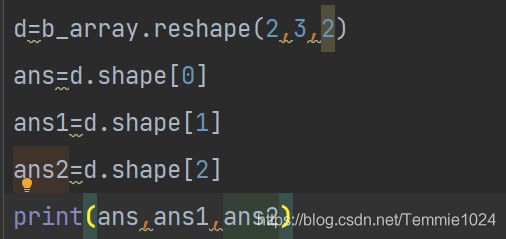
d=b_array.reshape(2,3,2)
print('c:','\n',c,'\n','d:','\n',d)
指定查询某一维度
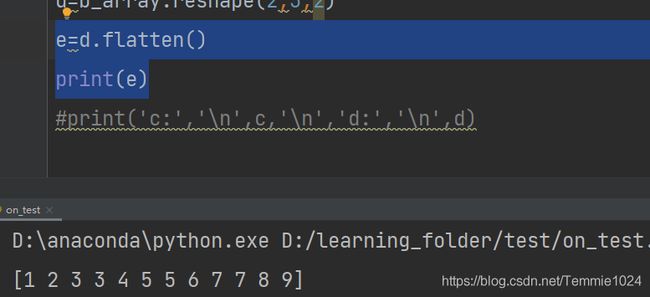
多维数组按行展开层一维数组flatten
e=d.flatten()
print(e)
数组计算
数组与数计算,数组中所有元素都应用数的计算。
import numpy
a=numpy.array([[0,1,2],[3,4,5]])
#h=numpy.array([[2,2,2],[2,2,2]])
b=a+2
c=a-2
d=a*2
e=a/2
f=a/0
print('a:','\n',a,'\n','b:','\n',b,'\n','c:','\n',c,'\n','d:','\n',d,'\n','e:','\n',e,'\n','f:','\n',f,'\n')
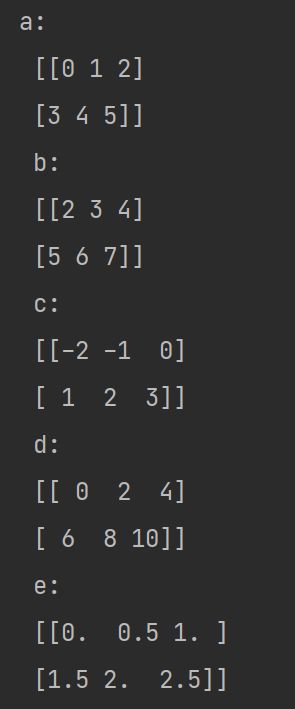
那么f呢?
和matlab一样,/0后出现正无穷(INF)和无效(NAN)两种情况

两个形状相同的数组,对应位置元素进行元素
import numpy
a=numpy.array([[0,1,2],[3,4,5]])
h=numpy.array([[2,4,6],[6,4,2]])
b=a+h
c=a-h
d=a*h
e=a/h
print('a:','\n',a,'\n','b:','\n',b,'\n','c:','\n',c,'\n','d:','\n',d,'\n','e:','\n',e)
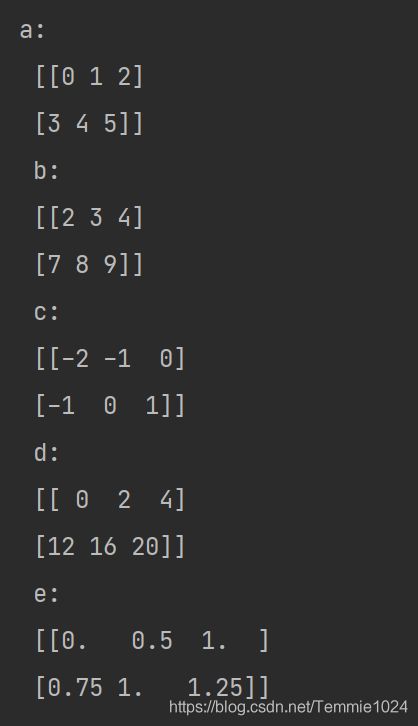
两个数组只有一个维度相同,在这个维度进行计算。
列数相同,每一行进行计算。
import numpy
a=numpy.array([[0,1,2],[3,4,5]])
h=numpy.array([2,4,6])
b=a+h
c=a-h
d=a*h
e=a/h
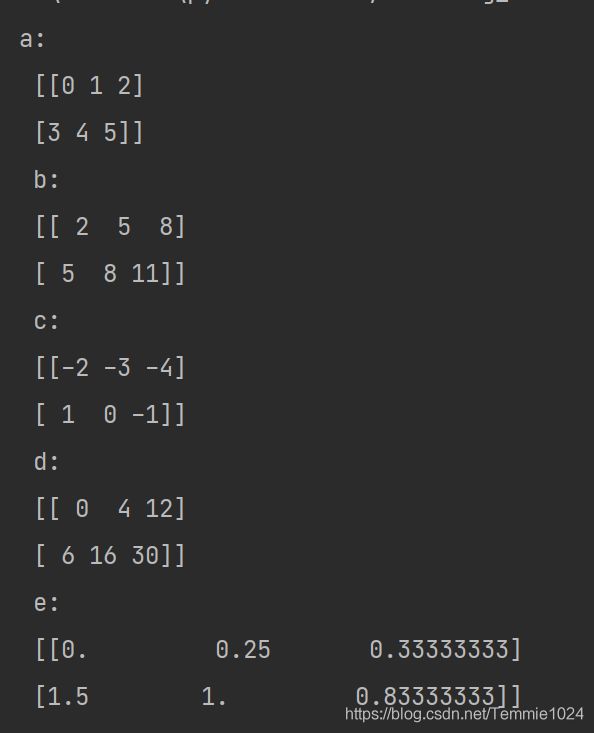
print('a:','\n',a,'\n','b:','\n',b,'\n','c:','\n',c,'\n','d:','\n',d,'\n','e:','\n',e)
import numpy
a=numpy.array([[0,1,2],[3,4,5]])
h=numpy.array([[2],[4]])
b=a+h
c=a-h
d=a*h
e=a/h
print('a:','\n',a,'\n','b:','\n',b,'\n','c:','\n',c,'\n','d:','\n',d,'\n','e:','\n',e)
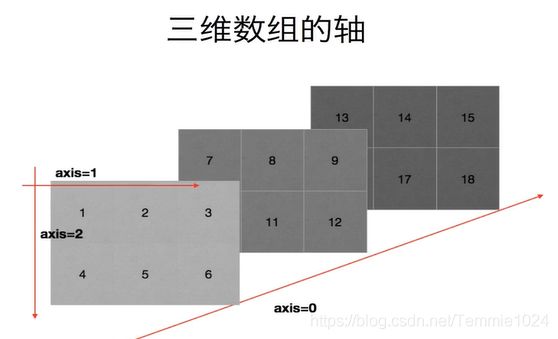
数组的轴
使用numpy读取数据
了解即可。一般不用。从文本问价读取。

fname文件位置
dtype读取出来的类型
delimiter数据用什么字符串分隔
skiprows跳过默写行,例如表头之类。
usecols读取指定的行
unpck是否转置
必须要写的fname、delimiter。如果读入数字较大,可以设置dtype。
数组操作
转置
transpsoe
import numpy
a=numpy.array([[1,2],[3,4]])
print('a:','\n',a)
b=a.transpose()
print('b:','\n',b)
import numpy
a=numpy.array([[1,2],[3,4]])
print('a:','\n',a)
b=a.T
c=a.swapaxes(1,0)
print('b:','\n',b)
print('c:','\n',c)
索引与切片
注意行列是从0开始数的
抽象表示:

第一个会取到对应的点,第二个是行列相交的位置。
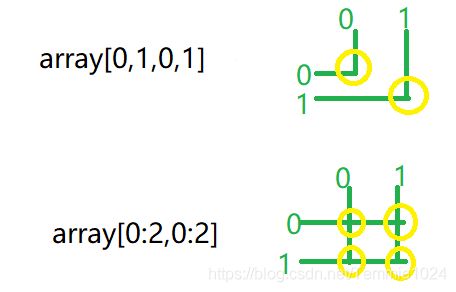
例子:
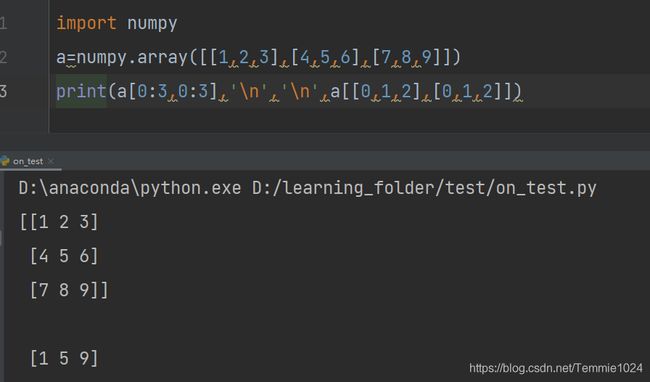
取某一行
import numpy
a=numpy.array([[1,2,3],[4,5,6],[7,8,9]])
print(a[0])
import numpy
a=numpy.array([[1,2,3],[4,5,6],[7,8,9]])
print(a[[0,2],:])
import numpy
a=numpy.array([[1,2,3],[4,5,6],[7,8,9]])
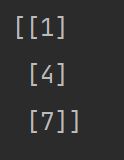
print(a[:,[0]])
import numpy
a=numpy.array([[1,2,3],[4,5,6],[7,8,9]])
print(a[:,[0,2]])
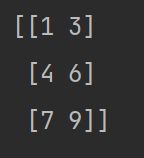
如果是连续多列也可以2:表示从第三列(行)开始到最后
如果是从2到4行(列),可以写作1:5
值的更改
直接取出赋值即可。
使用布尔来实现对数组中满足条件的值进行更改
假设现在的数组是:
1 2 3
4 5 6
7 8 9
我现在想把数组中的5取出修改成0
我们利用布尔值来判断满足条件的值在哪些位置,然后赋值即可。
import numpy
a=numpy.array([[1,2,3],[4,5,6],[7,8,9]])
a[a==5]=0
print(a)

除此之外还可以使用三元运算符进行赋值。这里给出一个numpy自带的函数,其他的常规三元运算符就不举例子了。
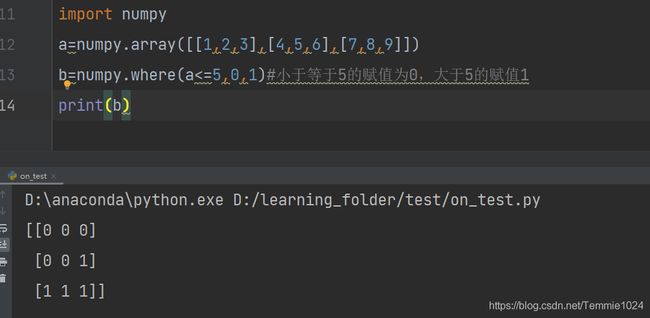
import numpy
a=numpy.array([[1,2,3],[4,5,6],[7,8,9]])
b=numpy.where(a<=5,0,1)#小于等于5的赋值为0,大于5的赋值1
print(b)
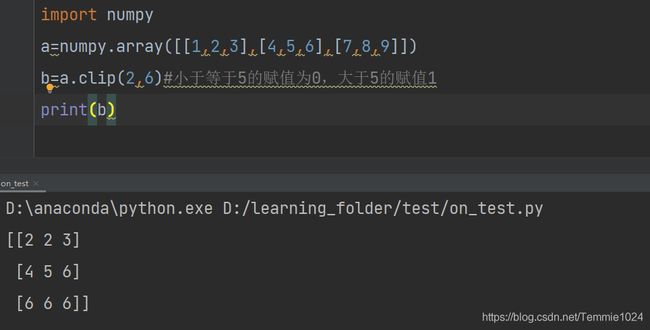
clip(a,b)裁剪操作
规定最小值a与最大值b,小于a的取a,大于b的取b
import numpy
a=numpy.array([[1,2,3],[4,5,6],[7,8,9]])
b=a.clip(2,6)#小于等于5的赋值为0,大于5的赋值1
print(b)
给元素赋值为NAN
NAN为浮点型,赋值前需要将数组类型转化为浮点型,然后赋值numpy.nan即可。
数组拼接
上下拼接与左右拼接
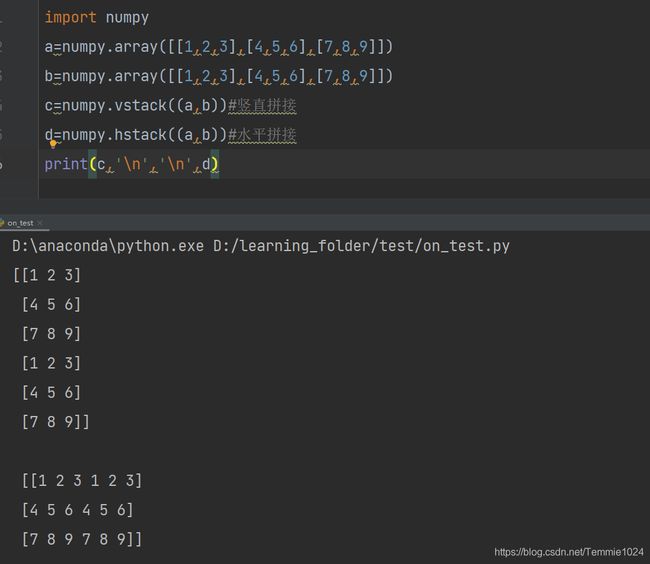
import numpy
a=numpy.array([[1,2,3],[4,5,6],[7,8,9]])
b=numpy.array([[1,2,3],[4,5,6],[7,8,9]])
c=numpy.vstack((a,b))#竖直拼接
d=numpy.hstack((a,b))#水平拼接
print(c,'\n','\n',d)
行交换与列交换
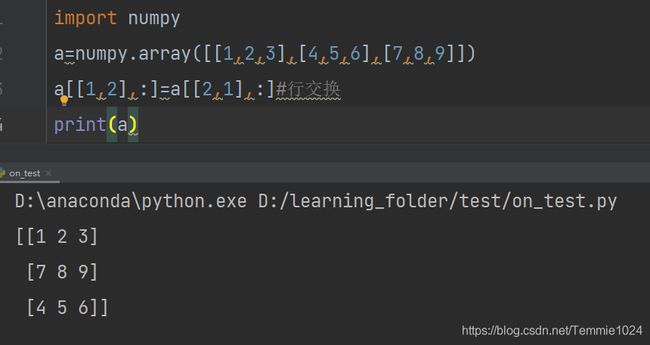
行交换
import numpy
a=numpy.array([[1,2,3],[4,5,6],[7,8,9]])
a[[1,2],:]=a[[2,1],:]#行交换
print(a)
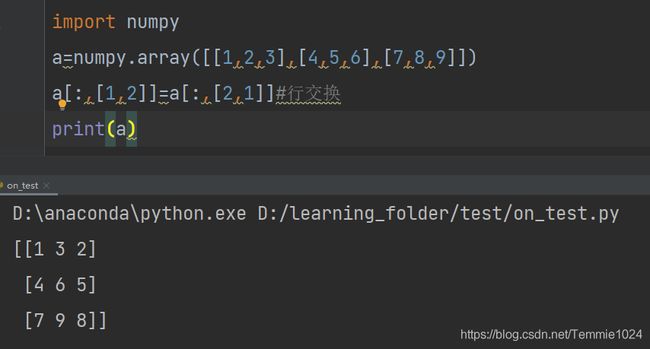
import numpy
a=numpy.array([[1,2,3],[4,5,6],[7,8,9]])
a[:,[1,2]]=a[:,[2,1]]#行交换
print(a)
NaN与Inf
nan与inf都是float类型
当我们读取本地的文件为float的时候,如果有缺失,就会出现nan
当做了一个不合适的计算的时候(比如无穷大(inf)减去无穷大)
不同位置的nan是不相等的,它本身也不是一个数值!
如何统计数组中nan的个数
numpy.count_nonzero(array!=array)可以统计nan的个数(array是指要统计的数组)。
这个语句把array!=array换成array==num即可统计等于num这个值的元素个数。

numpy常用的语法
axis就是上面的0,1,2
这里面t是数组,np是numpy的缩写(不可以直接用,要在import时as np才能这样写)

标准差是一组数据平均值分散程度的一种度量。一个较大的标准差,代表大部分数值和其平均值之间差异较大;一个较小的标准差,代表这些数值较接近平均值反映出数据的波动稳定情况,越大表示波动越大,越不稳定。

生成随机数numpy.random–