【梳理】离散数学 第19章 初等数论 19.1 素数 19.2 最大公约数和最小公倍数

教材：《离散数学》第2版 屈婉玲 耿素云 张立昂 高等教育出版社
源文档高清截图在最后

第19章 初等数论

本文用到的全部变量如无特别声明，均为整数。

19.1 素数

1、设整数a、b，且b≠0。如果存在整数c使得a = bc，就说a被b整除，或b整除a，记作b | a。也称a是b的倍数，b是a的因数（因子）。任何正整数都至少有两个因数：1和本身，称为平凡因子，其余称为真因子。

2、设整数a，b，且b≠0。存在唯一整数q和r，使得a = qb + r，0 ≤ r < |b|。该表达式称为带余除法，余数r = a mod b。计算机中取余常写成a % b，但按书本定义，余数是非负的（事实上余数可以为负），而计算机中取余时多用运算符 % 。对异号整数做 % 运算可能返回负整数，且绝对值根据语言的不同而不一定与两数绝对值做 % 运算时相同。两个同号整数做 % 运算时，模数才和余数相同。Matlab中，取余记为rem。为了方便，下面一般都将对两个非负数的取余写成a % b。
下面给出模数的定义：
模数 = 被除数－取整后的商×除数 商 = 被除数 / 除数，将商向负无穷大取整。Python 的 % 运算符为取模。
余数的定义：
余数 = 被除数－取整后的商×除数 商 = 被除数 / 除数，将商向零取整。C++ 的 % 运算符为取余。

3、不难验证，整除具有下列性质：
【1】若a | b且a | c，则对任意整数x，y都有a | xb + yc。
【2】若a | b且b | c，则a | c。
【3】设m≠0，则a | b当且仅当ma | mb。
【4】如果a | b且b | a，则a = ±b。
【5】如果a | b且b≠0，则 |a| ≤ |b|。
下面给出定义：如果正整数a大于1且只能被1和a自己整除，则a为质数（素数）。如果a > 1不是质数，则a为合数。1既不是质数也不是合数。下面四条性质中，p均为质数。
【6】如果d > 1且d | p，则d = p。
【7】若p | ab，则p | a或p | b。
设p | a1a2……ak，必存在1 ≤ i ≤ k使得p | ai。
【8】a > 1是合数当且仅当a = bc，其中a > b > 1，a > c > 1。
【9】合数一定有质因数。即a是一个合数，一定存在p使得p | a。

3、算术基本定理（唯一分解定理）设 a > 1，则，其中p1，p2，……，pk是不同的质数，r1，r2，……，rk是正整数。若不计顺序，该表达式是唯一的。这个表达式叫作质因数分解式（素因子分解式）。
这里不予证明。
有时候我们会用到唯一分解定理推广后的表达式：此时r1，r2，……，rk是非负整数，即可以等于0。当ri = 0时，相当于a不含质因数pi。对1而言，所有的ri等于0。
推论 a的因子根本上只含有a的素因子。用数学语言表达，一种写法是：
设，其中p1，p2，……，pk是不同的质数，r1，r2，……，rk是正整数。
正整数d为a的因子的充分必要条件是：。其中0 ≤ si ≤ ri，i = 1，2，……，k。

4、有无穷多个质数。
证明 设只有有限个质数，记为p1，p2，……，pn。设m =p1p2……pn + 1。显然pi % m≠0，1 ≤ i ≤ n。要么m是质数，要么m不是质数，但只有大于pn的质数才能整除m（合数m一定含有质因数），两者是矛盾的。证毕。

5、质数定理 ，π(n)代表 ≤ n的质数个数。证明超出课本《离散数学（第2版）》的范围，不予证明。
下表大致说明了质数的分布情况，可以看出当n越来越大时，小于等于n的质数的个数越来越接近n / ln(n)。

6、如果a是合数，则a必有一个 ≤ sqrt(a)的真因子。
证明 由整除的性质“a > 1是合数当且仅当a = bc，其中a > b > 1，a > c > 1”，显然b和c中一定有一个 ≤ sqrt(a)，否则bc > sqrt(a2) = a，矛盾。证毕。
推论 如果a是合数，则a必有一个 ≤ sqrt(a)的质因子。
证明 由上述证明，a = bc有 ≤ sqrt(a)的真因子b。如果b是质数，结论当然成立。如果b是合数，由整除的性质“如果b | a且a≠0，则 |b| ≤ |a| ”和“合数一定有质因数”，b有质因子p < b ≤ sqrt(a)。根据整除的传递性“若a | b且b | c，则a | c”，p也是a的因子，结论成立。

7、埃拉托斯特尼（Eratosthene）筛法（埃氏筛法） 要筛选出不大于n的质数，排除sqrt(n)以内全部质数的倍数即可。
C++代码示例见（前6543个质数 ≤ 65 535，正好能判断 ≤ 4 294 967 295的全部数是否为质数）：

const unsigned qty_of_prime = 6543;
unsigned prime[qty_of_prime] = {
      2, 3 };
inline void genprime() {
     
	unsigned a = 4, t; bool flag = true;
	for (unsigned i = 2; i < qty_of_prime;) {
     
		t = sqrt(a), flag = true;
		for (unsigned j = 0; prime[j] <= t; ++j) {
     
			if (a % prime[j] == 0) {
      flag = false; break; }
		}
		if (flag) {
      prime[i] = a, ++i; }
		++a;
	}
}
inline bool isprime(const unsigned& x) {
     
	if (x <= prime[qty_of_prime - 1])return binary_search(prime, prime + qty_of_prime, x);
	else {
     
		unsigned t = sqrt(x);
		for (unsigned j = 0; prime[j] <= t; ++j) {
     
			if (x % prime[j] == 0) {
      return false; }
		}
		return true;
	}
}

8、设质数p，形如2p－1的数称为梅森素数（Marin Mersenne Prime），目前已发现51个，第51个梅森素数为 282589933－1，由Patrick Laroche通过分布式计算项目大互联网梅森素数搜索（GIMPS）于2018年12月7日发现。

19.2 最大公约数与最小公倍数

1、设非零整数a，b，d，如果d | a且d | b，则d为a与b的公因数（公因子 / 公约数）。除了0，任何整数都只有有限个因子。两个不全为零的整数只有有限个公因子，最大的称作最大公因数，记作GCD(a, b)。

2、设a，b是两个非零整数，如果a | m且b | m，则称m为a与b的公倍数。a与b有无限个公倍数，最小的正公倍数称为最小公倍数，记作LCM(a, b)。

3、最大公因数和最小公倍数的性质：
（1）若整数a，b都能整除m，则a，b的最小公倍数也能整除m。
证明 即证：若a | m且b | m，则LCM(a, b) | m。
设M = LCM(a, b)，m = qM + r，0 ≤ r < M。根据整除的性质“若a | b且a | c，则对任意整数x，y都有a | xb + yc”，由a | m且a | M，及 r = m－qM，可推出a | r，同理b | r。所以r是a和b的公倍数。根据最小公倍数的定义，r = 0，所以M | m。
（2）若d能整除整数a，b，则d能整除a，b的最大公因数。
证明 即证：若d | a，d | b，则d | GCD(a, b)。
设D = GCD(a, b)，m = LCM(d, D)。当m = D时，自然有d | D，结论成立。否则，只能有m > D。而d | a且D | a（D是a，b的最大公因数），由（1）得m | a。同理m | b。即m是a和b的公因数，与D是a和b的最大公因数矛盾。证毕。
推论 这两个命题的逆命题都成立。
可以利用整数的质因数分解求最大公因数和最小公倍数。设a，b的质因数分解式

则

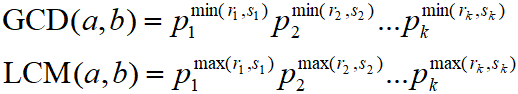
4、求最大公因数常用辗转相除法（欧几里得（Euclid）算法）。它是基于以下定理构造的：
设a = qb + r，a，b，q，r都是整数，则GCD(a, b) = GCD(b, r)。
证明 即证a和b与b和r有相同的公因数。设a与b有公因数d，即d | a且d | b。注意到r = a－qb，由整除的性质之一“若a | b且a | c，则对任意整数x，y都有a | xb + yc”，有d | r。从而d | b且d | r，即d也是b和r的公因数。反之一样，设b与r有公因数d，即d | b且d | r。注意到a = qb + r，故有d | a，从而d | a且d | b。证毕。
辗转相除法
设整数a，b且b≠0，做带余除法
a = q1r1 + r2，0 ≤ r2 < |r1|
若r2 > 0，再对b和r2做带余除法
r1 = q2r2 + r3，0 ≤ r3 < |r2|
重复上述过程。因为r1 > r2 > r3 > … ≥ 0，所以总是存在k使得rk+1 = 0，于是有：
a = q1r1 + r2，1 ≤ r2 < |r1|
r1 = q2r2 + r3，1 ≤ r3 < |r2|
r2 = q3r3 + r4，1 ≤ r4 < |r3|
……
rk-2 = qk-1rk-1 + rk，1 ≤ rk-1 < |rk-1|
rk-1 = qkrk + rk+1 = qkrk + 0
而GCD(a, b) = GCD(b, r)，所以GCD(a, r1) = GCD(r1, r2) = … = GCD(rk-1, rk) = rk
当b ≤ int(a / 2) 时，a % b ≤ int(a / 2)，当b > int(a / 2)时，因为a / b < 2，所以a % b ≤ int(a / 2)。可见，a % b ≤ int(a / 2) 总成立。最坏情况时，每次取模的结果都为int(a / 2)，所以该算法的时间复杂度不超过O(log2n)。

5、扩展欧几里得算法 设a和b不全为0，则存在整数x和y使得GCD(a, b) = xa + yb。
证明 设a = r0，b = r1，将辗转相除法中的计算过程改写成：
ri = qi+1ri+1 + ri+2，i = 0, 1, …, k－2
rk-1 = qkrk + rk+1 = qkrk + 0

GCD(a, b) = rk。上式改写成
ri = ri-2－qi-1ri-1，i = 2, 3, …, k
从后向前逐个回代，就可以将rk表示成a和b的线性组合。
设xk-1 = 1，yk-1 = －qk-1，则上式可以写成
rk = xk-1rk-2 + yk-1rk-1
尝试设一般情况rk = xi-1ri-2 + yiri，并代入ri = ri-2－qi-1ri-1，得
rk = xi-1ri-2 + yir(ri-2－qi-1ri-1) = yiri-2 + (xi－qi-1yi)ri-1
将rk = yiri-2 + (xi－qi-1yi)ri-1与rk = xi-1ri-2 + yiri对比，得
xi-1 = yi，yi-1 = xi－qi-1yi，i = k－1，k－2，……，2
记x = x1，y = y1，就得rk = xa + yb。
可见，要执行扩展欧几里得算法，需要先执行欧几里得算法得到GCD(a, b) = rk = rk-2－qk-1rk-1，然后设xk-1 = 1，yk-1 = －qk-1，再根据递推式xi-1 = yi，yi-1 = xi－qi-1yi，来求得符合GCD(a, b) = xa + yb的解x，y。

6、如果GCD(a, b) = 1，则a与b互质（互素）。如果一系列整数的任意两个互质，就说它们两两互质。

7、整数a和b互质的充分必要条件是：存在整数x和y使得xa + yb = 1。
证明 必要性（左推右）可由上述对扩展欧几里得算法的证明直接得到。
充分性（右推左）。设整数x，y满足xa + yb = 1，设d > 0是a和b的一个公因数，由性质“若a | b且a | c，则对任意整数x，y都有a | xb + yc”，所以d | xa + yb，即d | 1，于是d只能取1。证毕。

例19.5 设a | c且b | c，且a和b互质，则ab | c。
证明 根据互质的充要条件，存在整数x，y使得xa + yb = 1。两边同乘c得cxa + cyb = c。而a | xa，b | c（已知），所以ab | bxa，所以ab | cxa。同理ab | cyb。根据性质“若a | b且a | c，则对任意整数x，y都有a | xb + yc”，于是ab | cxa + cyb即ab | c。