数字图像处理_04_(图像模糊（滤波））

1.卷积

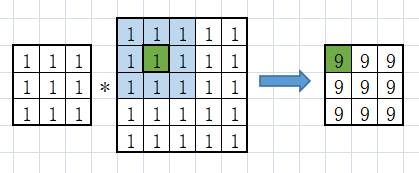
卷积在图像处理中的应用是输入一幅图像$f(x,y)$，经过特定设计的卷积核$g(x,y)$进行卷积处理以后，输出图像将会得到模糊，边缘强化等各种效果。图像处理的卷积的原理如图：

由一个 卷积核 与一个 图像 进行 元素对应相乘再累和。
当图片较大时：

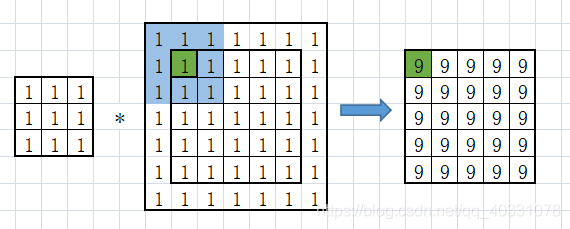
可见卷积之后原图像尺寸发生变化，由原来的5 * 5变为了3 * 3，而在图像处理的多数情况下是要保持图像尺寸的，为此要对原图像进行边缘扩展后(OpenCV中会自行完成边缘扩展)再进行卷积，例如先将5 * 5扩展为7 * 7，则更改后就可以保持原尺寸5 * 5。

先给出图像添加噪声的模拟算法

import numpy as np
import matplotlib.pyplot as plt
import cv2 as cv
#读取图片
img=cv.imread('../pic/cat200x192.jpg')
#获取图片长宽
w,h,c=img.shape
#随机产生500个白色的像素噪声点
for i in range(500):
    x=np.random.randint(0,w)
    y=np.random.randint(0,h)
    img[x,y,:]=255
#保存图片
cv.imwrite('../pic/cat_noise.png',img)
plt.imshow(img)
plt.show()

输出结果如下图：

这里将提到在图像处理中常用到的图像模糊方法，有均值滤波，中值滤波，高斯模糊。

2.均值模糊(滤波)

1）原理：均值滤波是典型的线性滤波算法，它是指在图像上对目标像素给一个模板，该模板包括了其周围的临近像素（以目标像素为中心的周围8个像素，构成一个滤波模板，即包括目标像素本身），再用模板中的全体像素的平均值来代替原来像素值。
均值滤波的卷积核模板一般为：
$$K=\frac{1}{9}\left[\begin{array}{ccc}1& 1& 1\\ 1& 1& 1\\ 1& 1& 1\end{array}\right]$$
代码如下：

import numpy as np
import matplotlib.pyplot as plt
import cv2 as cv
#自定义一个读取图像函数
def show(img):
    if img.ndim==2:
        plt.imshow(img,cmap='gray')
    else:
        img2=cv.cvtColor(img,cv.COLOR_BGR2RGB)
        plt.imshow(img2)
    plt.show()
#读取图片
img=cv.imread('../pic/cat_noise.png')
#分别3*3和7*7的卷积核进行均值模糊
img2=cv.blur(img,(3,3))
img3=cv.blur(img,(7,7))
#显示图片
show(np.hstack([img,img2,img3]))

输出结果如下图(原图，卷积核为3 * 3，卷积核为7 * 7)：

PS：
1.均值滤波卷积核尺寸n越大，图像越模糊。
2.卷积核一般为n为奇数的矩阵，这里给出3*3的模板：$$K=\frac{1}{9}\left[\begin{array}{ccc}1& 1& 1\\ 1& 1& 1\\ 1& 1& 1\end{array}\right]$$
3 cv.blur(原图像，卷积核尺寸)卷积核尺寸表示为（3,3），（5,5）。

3.中值模糊(滤波)

原理：中值滤波法是一种非线性平滑技术，它将每一像素点的灰度值设置为该点某邻域窗口内的所有像素点灰度值的中值.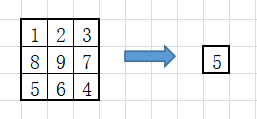

代码如下：

import numpy as np
import matplotlib.pyplot as plt
import cv2 as cv
#自定义一个读取图像函数
def show(img):
    if img.ndim==2:
        plt.imshow(img,cmap='gray')
    else:
        img2=cv.cvtColor(img,cv.COLOR_BGR2RGB)
        plt.imshow(img2)
    plt.show()
#读取图片
img=cv.imread('../pic/cat_noise.png')
#分别3*3和5*5的卷积核进行中值模糊
img2=cv.medianBlur(img,3)
img3=cv.medianBlur(img,5)
show(np.hstack([img,img2,img3]))

输出结果如下图：

PS：
1.中值滤波卷积核尺寸n越大，图像越模糊。
2.卷积核一般为n为奇数的矩阵，卷积核无固定模板，
3 .img_medianBlur=cv.medianBlur(原图像，卷积核阶数)卷积核尺寸表示为3，5。

4.高斯模糊(滤波)

原理：高斯滤波是一种线性平滑滤波，适用于消除高斯噪声，广泛应用于图像处理的减噪过程。高斯滤波就是对整幅图像进行加权平均的过程，每一个像素点的值，都由其本身和邻域内的其他像素值经过加权平均后得到。高斯滤波的具体操作是：用一个模板（或称卷积、掩模）扫描图像中的每一个像素，用模板确定的邻域内像素的加权平均灰度值去替代模板中心像素点的值。
高斯滤波卷积核模板
$$K=\frac{1}{16}\left[\begin{array}{ccc}1& 2& 1\\ 2& 4& 2\\ 1& 2& 1\end{array}\right]$$
代码如下：

import numpy as np
import matplotlib.pyplot as plt
import cv2 as cv
#自定义一个读取图像函数
def show(img):
    if img.ndim==2:
        plt.imshow(img,cmap='gray')
    else:
        img2=cv.cvtColor(img,cv.COLOR_BGR2RGB)
        plt.imshow(img2)
    plt.show()
#读取图片
img=cv.imread('../pic/cat_noise.png')
#分别3*3和5*5的卷积核进行高斯模糊
img2=cv.GaussianBlur(img,(3,3),sigmaX=100)
img3=cv.GaussianBlur(img,(5,5),sigmaX=100)
show(np.hstack([img,img2,img3]))

输出结果如下：
同时在相同尺寸不同$\sigma$的情况下有如下结果（原图，sigma为0.1，100）：

PS：
1.cv.GaussianBlur(原图像,卷积核尺寸,X方向方差)
卷积核尺寸表示为（3,3）
只写sigmaX，sigmaY缺省相同
2.高斯滤波卷积核尺寸n越大，越模糊。
3.高斯滤波sigma越小越接近原图，越大越模糊。
4.常用的卷积核模板为：$$K=\frac{1}{16}\left[\begin{array}{ccc}1& 2& 1\\ 2& 4& 2\\ 1& 2& 1\end{array}\right]$$