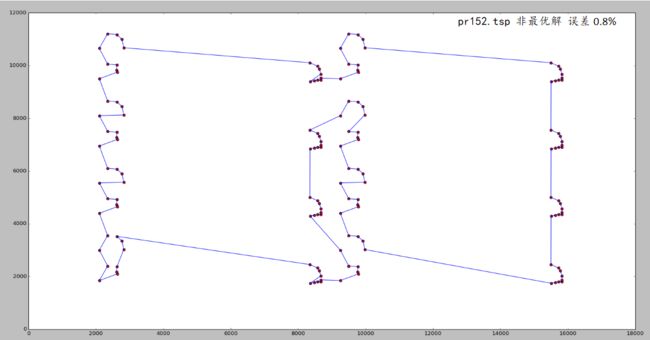
旅行推销员问题(Travelling salesman problem, TSP)是这样一个问题:给定一系列城市和每对城市之间的距离,求解访问每一座城市一次并回到起始城市的最短回路。
它是组合优化中的一个NP困难问题,在运筹学和理论计算机科学中非常重要。
蚁群算法(Ant Colony Optimization, ACO),又称蚂蚁算法,是一种用来在图中寻找优化路径的机率型算法,对蚂蚁行为进行模仿抽象。在求解旅行推销员问题时,蚂蚁随机从某一城市出发,根据城市间距离与残留信息素浓度按概率选择下一城市,蚂蚁走完所有的城市后,在走过的路径上留下信息素,蚂蚁走的总路程越少,留下的信息素就越多。多次循环后,最好的路径就有可能被筛选出。
- 早先接触蚁群算法,最近重新回顾,感觉颇有意思。它对数学要求不高,没有多少公式,容易理解。不过实力浅薄,仅分享一下个人尝试和资料,供感兴趣的人探索。
- 在代码实现上,主要为蚁群和蚂蚁两个对象,简洁清晰,感觉是良好的教学材料。
-
此外,蚁群算法结合pygame做成可视化效果,对于小朋友的吸引力应该很大,:)
运行尝试
- github 下载,解压后
python Xant.py或python XantPro.py运行即可,动态查看当前求解效果。
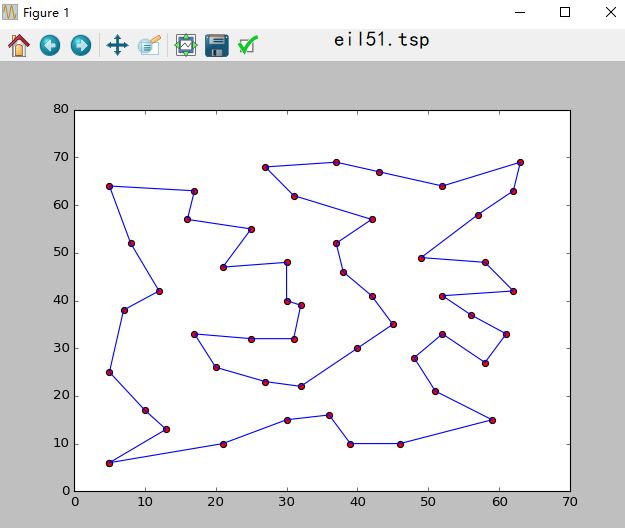
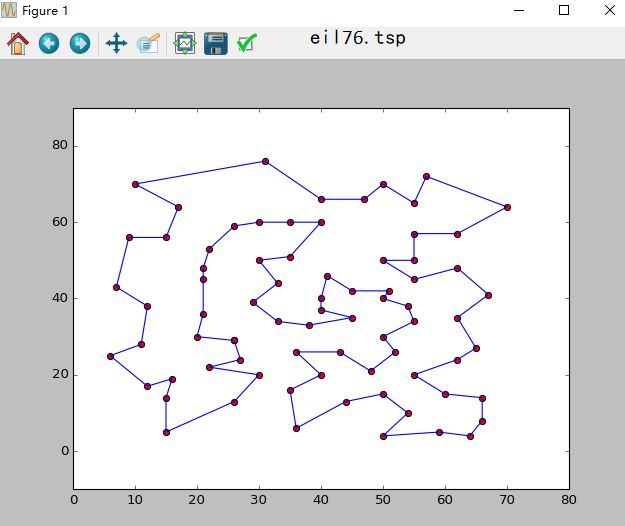
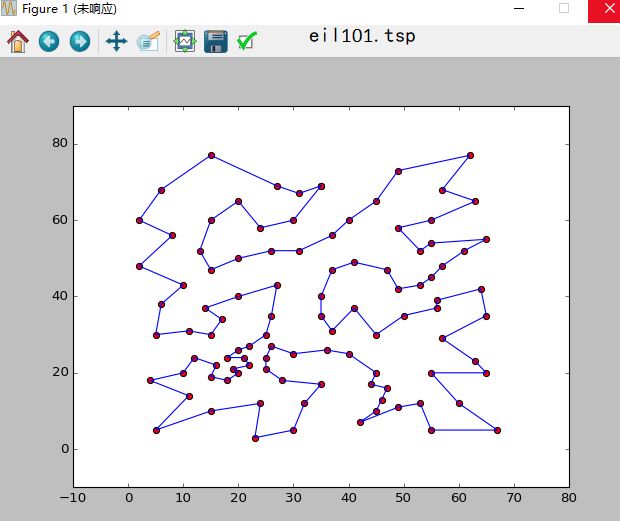
求解效果图
-
eil51城市数据下载地址
-
其他城市数据下载地址
代码1
- 老版详细注释,代码质量不高,便于理解:
# -*- coding: UTF-8 -*-
'''
程序主体:
类BACA的实例化->类BACA的初始化->执行BACA.ReadCityInfo()方法->执行BACA.Search()方法->执行BACA.PutAnts()方法
->类ANT的初始化->类ANT的实例化->执行ANT.MoveToNextCity()方法->执行ANT.SelectNextCity()方法->执行ANT.AddCity()方法
->执行ANT.UpdatePathLen()方法->执行BACA.UpdatePheromoneTrail()方法
蚁群算法中关键两个问题,一个是选择下一个城市的算法,主要在ANT.SelectNextCity(self, alpha, beta)方法中,其中alpha为表征
信息素重要程度的参数,beta为表征启发式因子重要程度的参数;而更新信息素主要在BACA.UpdatePheromoneTrail(self)方法中。
'''
import os, sys, random#调入基本的python模块
from math import *
import pylab as pl
BestTour = []#用于放置最佳路径选择城市的顺序
CitySet = set()#sets数据类型是个无序的、没有重复元素的集合,两个sets之间可以做差集,即在第一个集合中移出第二个集合中也存在的元素
CityList = []#城市列表即存放代表城市的序号
PheromoneTrailList = []#信息素列表(矩阵)
PheromoneDeltaTrailList = []#释放信息素列表(矩阵)
CityDistanceList = []#两两城市距离列表(矩阵)
AntList = []#蚂蚁列表
class BACA:#定义类BACA,执行蚁群基本算法
def __init__(self, cityCount=51, antCount=51, q=80, alpha=1, beta=3, rou=0.4, nMax=100):
#self, cityCount=51, antCount=50, q=80, alpha=2, beta=5, rou=0.3, nMax=40
#初始化方法,antCount为蚂蚁数,nMax为迭代次数
self.CityCount = cityCount#城市数量,本例中为手工输入,也可以根据城市数据列表编写程序获得
self.AntCount = antCount#蚂蚁数量
self.Q = q#信息素增加强度系数
self.Alpha = alpha#表征信息素重要程度的参数
self.Beta = beta#表征启发因子重要程度的参数
self.Rou = rou#信息素蒸发系数
self.Nmax = nMax#最大迭代次数
self.Shortest = 10e6#初始最短距离应该尽可能大,至少大于估算的最大城市旅行距离
random.seed()#设置随机种子
#初始化全局数据结构及值
for nCity in range(self.CityCount):#循环城市总数的次数(即循环range(0,51),为0-50,不包括51)
BestTour.append(0)#设置最佳路径初始值均为0
for row in range(self.CityCount):#再次循环城市总数的次数
pheromoneList = []#定义空的信息素列表
pheromoneDeltaList = []#定义空的释放信息素列表
for col in range(self.CityCount):#循环城市总数的次数
pheromoneList.append(100)#定义一个城市到所有城市路径信息素的初始值
pheromoneDeltaList.append(0)#定义一个城市到所有城市路径释放信息素的初始值
PheromoneTrailList.append(pheromoneList)#建立每个城市到所有城市路径信息素的初始值列表矩阵
PheromoneDeltaTrailList.append(pheromoneDeltaList)#建立每个城市到所有城市路径释放信息素的初始值列表矩阵
def ReadCityInfo(self, fileName):#定义读取城市文件的方法
file = open(fileName)#打开城市文件
for line in file.readlines():#逐行读取文件
cityN, cityX, cityY = line.split()#分别提取城市序号、X坐标和Y坐标,使用空格切分
CitySet.add(int(cityN))#在城市集合中逐步追加所有的城市序号
CityList.append((int(cityN), float(cityX), float(cityY)))#在城市列表中逐步追加每个城市序号、X坐标和Y坐标建立的元组
for row in range(self.CityCount):#循环总城市数的次数
distanceList = []#建立临时储存距离的空列表
for col in range(self.CityCount):
distance = sqrt(pow(CityList[row][1]-CityList[col][1], 2) + pow(CityList[row][2]-CityList[col][2], 2))#逐一计算每个城市到所有城市的距离值
distance = round(distance)
distanceList.append(distance)#追加一个城市到所有城市的距离值
CityDistanceList.append(distanceList)#追加么个城市到所有城市的距离值,为矩阵,即包含子列表
file.close()#关闭城市文件
def PutAnts(self):#定义蚂蚁所选择城市以及将城市作为参数定义蚂蚁的方法和属性
AntList.clear() # 先清空列表
for antNum in range(self.AntCount):#循环蚂蚁总数的次数
city = random.randint(1, self.CityCount)#随机选择一个城市
ant = ANT(city)#蚂蚁类ANT的实例化,即将每只蚂蚁随机选择的城市作为传入的参数,使之具有ANT蚂蚁类的方法和属性
AntList.append(ant)#将定义的每只蚂蚁追加到列表中
def Search(self):#定义搜索最佳旅行路径方法的主程序
for iter in range(self.Nmax):#循环指定的迭代次数
self.PutAnts()#执行self.PutAnts()方法,定义蚂蚁选择的初始城市和蚂蚁具有的方法和属性
for ant in AntList:#循环遍历蚂蚁列表,由self.PutAnts()方法定义获取
for ttt in range(len(CityList)):#循环遍历城市总数次数
ant.MoveToNextCity(self.Alpha, self.Beta)#执行蚂蚁的ant.MoveToNextCity()方法,获取蚂蚁每次旅行时的旅行路径长度CurrLen,禁忌城市城市列表TabuCityList等属性值
ant.two_opt_search()#使用邻域优化算法 $$$
ant.UpdatePathLen()#使用ant.UpdatePathLen更新蚂蚁旅行路径长度
tmpLen = AntList[0].CurrLen#将蚂蚁列表中第一只蚂蚁的旅行路径长度赋值给新的变量tmplen
tmpTour = AntList[0].TabuCityList#将获取的蚂蚁列表的第一只蚂蚁的禁忌城市列表赋值给新的变量tmpTour
for ant in AntList[1:]:#循环遍历蚂蚁列表,从索引值1开始,除第一只外
if ant.CurrLen < tmpLen:#如果循环到的蚂蚁旅行路径长度小于tmpLen即前次循环蚂蚁旅行路径长度,开始值为蚂蚁列表中第一只蚂蚁的旅行路径长度
tmpLen = ant.CurrLen#更新变量tmpLen的值
tmpTour = ant.TabuCityList#更新变量tmpTour的值,即更新禁忌城市列表
if tmpLen < self.Shortest:#如果从蚂蚁列表中获取的最短路径小于初始化时定义的长度
self.Shortest = tmpLen#更新旅行路径最短长度
BestTour = tmpTour #更新初始化时定义的最佳旅行城市次序列表
print(iter,":",self.Shortest,":",BestTour)#打印当前迭代次数、最短旅行路径长度和最佳旅行城市次序列表
self.UpdatePheromoneTrail()#完成每次迭代需要使用self,UpdatePheromoneTrail()方法更新信息素
#画图查看结果
x = []; y = []
for city in BestTour:
x.append(CityList[city-1][1])
y.append(CityList[city-1][2])
x.append(x[0])
y.append(y[0])
pl.plot(x, y)
#pl.figure()
pl.scatter(x, y)
pl.show()
def UpdatePheromoneTrail(self):#定义更新信息素的方法,需要参考前文对于蚁群算法的阐述
for ant in AntList:#循环遍历蚂蚁列表
for city in ant.TabuCityList[0:-1]:#循环遍历蚂蚁的禁忌城市列表
idx = ant.TabuCityList.index(city)#获取当前循环 禁忌城市的索引值
nextCity = ant.TabuCityList[idx+1]#获取当前循环禁忌城市紧邻的下一个禁忌城市
PheromoneDeltaTrailList[city-1][nextCity-1] += self.Q / ant.CurrLen
#逐次更新释放信息素列表,注意矩阵行列所代表的意义,[city-1]为选取的子列表即当前城市与所有城市间路径的
#释放信息素值,初始值均为0,[nextCity-1]为在子列表中对应紧邻的下一个城市,释放信息素为Q,信息素增加强度
#系数与蚂蚁当前旅行路径长度CurrLen的比值,路径长度越小释放信息素越大,反之则越小。
PheromoneDeltaTrailList[nextCity-1][city-1] += self.Q / ant.CurrLen
#在二维矩阵中,每个城市路径均出现两次,分别为[city-1]对应的[nextCity-1]和[nextCity-1]对应的[city-1],因此都需要更新,
#注意城市序列因为从1开始,而列表索引值均从0开始,所以需要减1
lastCity = ant.TabuCityList[-1]#获取禁忌城市列表的最后一个城市
firstCity = ant.TabuCityList[0]#获取禁忌城市列表的第一个城市
PheromoneDeltaTrailList[lastCity-1][firstCity-1] += self.Q / ant.CurrLen
#因为蚂蚁旅行需要返回开始的城市,因此需要更新禁忌城市列表最后一个城市到第一个城市旅行路径的释放信息素值,即最后一个城市对应第一个城市的释放信息素值
PheromoneDeltaTrailList[firstCity-1][lastCity-1] += self.Q / ant.CurrLen
#同理更新第一个城市对应最后一个城市的释放信息素值
for (city1, city1X, city1Y) in CityList:#循环遍历城市列表,主要是提取city1即城市的序号
for (city2, city2X, city2Y) in CityList:#再次循环遍历城市列表,主要是提取city2即城市序号,循环两次的目的仍然是对应列表矩阵的数据结构
PheromoneTrailList[city1-1][city2-1] = ( (1-self.Rou)*PheromoneTrailList[city1-1][city2-1] + PheromoneDeltaTrailList[city1-1][city2-1] )
PheromoneDeltaTrailList[city1-1][city2-1] = 0#将释放信息素列表值再次初始化为0,用于下次循环
#### print(PheromoneTrailList)
class ANT:#定义蚂蚁类,使得蚂蚁具有相应的方法和属性
def __init__(self, currCity = 0):#蚂蚁类的初始化方法,默认传入当前城市序号为0
self.TabuCitySet = set()
#定义禁忌城市集合,定义集合的目的是集合本身要素不重复并且之间可以做差集运算,例如AddCity()方法中
#self.AllowedCitySet = CitySet - self.TabuCitySet,可以方便地从城市集合中去除禁忌城市列表的城市,获取允许的城市列表
self.TabuCityList = []#定义禁忌城市空列表
self.AllowedCitySet = set()#定义允许城市集合
self.TransferProbabilityList = []#定义城市选择可能性列表
self.CurrCity = 0 #定义当前城市初始值为0
self.CurrLen = 0.0#定义当前旅行路径长度
self.AddCity(currCity)#执行AddCity()方法,获取每次迭代的当前城市CurrCity、禁忌城市列表TabuCityList和允许城市列表AllowedCitySet的值
pass#空语句,此行为空,不运行任何操作
def SelectNextCity(self, alpha, beta):#定义蚂蚁选择下一个城市的方法,需要参考前文描述的蚁群算法
if len(self.AllowedCitySet) == 0:#如果允许城市集合为0,则返回0
return (0)
sumProbability = 0.0#定义概率,可能性初始值为0
self.TransferProbabilityList = []#建立选择下一个城市可能性空列表
for city in self.AllowedCitySet:#循环遍历允许城市集合
sumProbability = sumProbability + (
pow(PheromoneTrailList[self.CurrCity-1][city-1], alpha) *
pow(1.0/CityDistanceList[self.CurrCity-1][city-1], beta)
)
#蚂蚁选择下一个城市的可能性由信息素与城市间距离之间关系等综合因素确定,其中alpha为表征信息素重要程度的参数,beta为表征启发式因子重要程度的参数,
#该语句为前文蚁群算法阐述的选择下一个转移城市的概率公式的分母部分
transferProbability = sumProbability#根据信息素选择公式和轮盘选择得出概率列表,非0-1
self.TransferProbabilityList.append((city, transferProbability))#将城市序号和对应的转移城市概率追加到转移概率列表中
threshold = sumProbability * random.random()#将概率值乘以一个0~1的随机数,获取轮盘指针值
for (cityNum, cityProb) in self.TransferProbabilityList:#再次循环遍历概率列表
if threshold <= cityProb:#如果轮盘指针值大于概率值,则返回对应的城市序号
#!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! key step!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
return (cityNum)
return (0)#否则返回0
def MoveToNextCity(self, alpha, beta):#定义转移城市方法
nextCity = self.SelectNextCity(alpha, beta)#执行SelectNextCity(),选择下一个城市的方法,获取选择城市的序号,并赋值给新的变量nextCity
if nextCity > 0 : #如果选择的城市序号大于0,则执行self.AddCity()方法,获取每次迭代的当前城市Currcity、禁忌城市列表TabuCityList和允许城市列表AllowedCitySet的值
self.AddCity(nextCity)#执行self.AddCity()方法
def ClearTabu(self):#定义清楚禁忌城市方法,以用于下一次循环
self.TabuCityList = []#初始化禁忌城市列表为空
self.TabuCitySet.clear()#初始化城市禁忌列表为空
self.AllowedCitySet = CitySet - self.TabuCitySet#初始化允许城市集合
def UpdatePathLen(self):#定义更新旅行路径长度方法
for city in self.TabuCityList[0:-1]:#循环遍历禁忌城市列表
nextCity = self.TabuCityList[self.TabuCityList.index(city)+1]#获取禁忌城市列表中的下一个城市序号
self.CurrLen = self.CurrLen + CityDistanceList[city-1][nextCity-1]#从城市间距离之中提取当前循环城市与下一个城市之间的距离,并逐次求和
lastCity = self.TabuCityList[-1]#提取禁忌列表中的最后一个城市
firstCity = self.TabuCityList[0]#提取禁忌列表中的第一个城市
self.CurrLen = self.CurrLen + CityDistanceList[lastCity-1][firstCity-1]#将最后一个城市与第一个城市的距离值加到当前旅行路径长度,获取循环全部城市的路径长度
def AddCity(self, city):#定义增加城市到禁忌城市列表中的方法
if city <= 0:#如果城市序号小于等于0,则返回
return
self.CurrCity = city#更新当前城市序号
self.TabuCityList.append(city)#将当前城市追加到禁忌城市列表中,因为已经旅行过的城市不应该再进入
self.TabuCitySet.add(city)#将当前城市追加到禁忌城市集合中,用于差集运算
self.AllowedCitySet = CitySet - self.TabuCitySet#使用集合差集的方法获取允许的城市列表
def two_opt_search(self): # 领域搜索
cityNum = len(CityList)
for i in range(cityNum):
for j in range(cityNum-1, i, -1):
#for j in range(i+1, cityNum):
#for j in range((i+10) if (i+10)代码2
- 去除注释,美化代码,增加了最大最小蚁群规则(详见文末资料),求解效果变好
# -*- coding: UTF-8 -*-
import random
from math import pow, sqrt
import numpy as np
import pandas as pd
import pylab as pl
class MMAS:
def __init__(self, antCount=20, q=100, alpha=1, beta=3,
rou=0.3, initialph=10, nMax=10000):
'''
https://svn-d1.mpi-inf.mpg.de/AG1/MultiCoreLab/papers/StuetzleHoos00%20-%20MMAS.pdf
'''
self.AntCount = antCount
self.Q = q
self.Alpha = alpha
self.Beta = beta
self.Rou = rou
self.initialPh = initialph
self.Nmax = nMax
self.Shortest = float('inf')
self.AntList = []
pl.show()
def ReadCityInfo(self, fileName):
'''
http://stackoverflow.com/questions/29281680/numpy-individual-element-access-slower-than-for-lists
'''
city_info = pd.read_csv(fileName,
sep=' ',
skiprows=6, skipfooter=1,
engine='python',
header=None,
names=('N', 'x', 'y'))
self.CityCount = city_info.shape[0]
self.CitySet = set()
self.CityDistance = [
[0] * self.CityCount for i in range(self.CityCount)]
self.CityDistanceBeta = np.zeros(
(self.CityCount, self.CityCount)).tolist()
self.Pheromone = [
[self.initialPh] * self.CityCount for i in range(self.CityCount)]
self.PheromoneDelta = np.zeros(
(self.CityCount, self.CityCount)).tolist()
self.BestTour = [None] * self.CityCount
for row in city_info.index:
for col in city_info.index:
if row != col:
distance = round(
sqrt(pow(city_info.x[row] - city_info.x[col], 2)
+ pow(city_info.y[row] - city_info.y[col], 2))
)
self.CityDistance[row][col] = distance
self.CityDistanceBeta[row][col] = pow(
1.0 / distance, self.Beta)
self.city_info = city_info
def PutAnts(self):
self.AntList.clear()
for antNum in range(self.AntCount):
city = random.choice(self.city_info.index)
ant = ANT(city, self.city_info.index,
self.CityDistance, self.Pheromone)
self.AntList.append(ant)
def Search(self):
import time
for iter in range(self.Nmax):
start = time.time()
self.PutAnts()
tmpLen = float('inf')
tmpTour = []
for ant in self.AntList:
for ttt in range(self.CityCount):
ant.MoveToNextCity(self.Alpha, self.Beta)
ant.two_opt_search()
ant.UpdatePathLen()
if ant.CurrLen < tmpLen:
self.bestAnt = ant
tmpLen = ant.CurrLen
tmpTour = ant.TabuCityList
if tmpLen < self.Shortest:
self.Shortest = tmpLen
self.BestTour = tmpTour
print(iter, "-->", self.Shortest, "-->", self.BestTour)
# self.bestAnt.two_opt_search()
self.UpdatePheromoneTrail()
end = time.time()
print(end - start)
pl.clf()
x = []; y = []
for city in self.BestTour:
x.append(self.city_info.x[city])
y.append(self.city_info.y[city])
x.append(x[0])
y.append(y[0])
pl.plot(x, y)
pl.scatter(x, y, s=30, c='r')
pl.pause(0.01)
def UpdatePheromoneTrail(self):
ant = self.bestAnt
pheromo_new = self.Q / ant.CurrLen
tabu = ant.TabuCityList
PD = self.PheromoneDelta
P = self.Pheromone
citys = self.city_info.index
for city, nextCity in zip(tabu[:-1], tabu[1:]):
PD[city][nextCity] = pheromo_new
PD[nextCity][city] = pheromo_new
lastCity = tabu[-1]
firstCity = tabu[0]
PD[lastCity][firstCity] = pheromo_new
PD[firstCity][lastCity] = pheromo_new
for c1 in citys:
for c2 in citys:
if c1 != c2:
P[c1][c2] = (
(1 - self.Rou) * P[c1][c2]
+ PD[c1][c2]
)
if P[c1][c2] < 0.001:
P[c1][c2] = 0.001
if P[c1][c2] > 10:
raise(Exception('too big Ph'))
P[c1][c2] = 10
PD[c1][c2] = 0
class ANT:
def __init__(self, currCity=0, citys=None, cityDis=None, pheromo=None):
self.TabuCityList = [currCity, ]
self.AllowedCitySet = set(citys)
self.AllowedCitySet.remove(currCity)
self.CityDistance = cityDis
self.Pheromone = pheromo
self.TransferProbabilityList = []
self.CurrCity = currCity
self.CurrLen = 0
def SelectNextCity(self, alpha, beta):
if self.AllowedCitySet:
sumProbability = 0
self.TransferProbabilityList = []
for city in self.AllowedCitySet:
sumProbability = sumProbability + (
pow(self.Pheromone[self.CurrCity][city], alpha) *
pow(1.0 /
self.CityDistance[self.CurrCity][city], beta)
)
transferProbability = sumProbability
self.TransferProbabilityList.append(
(city, transferProbability))
threshold = sumProbability * random.random()
#~print(self.TransferProbabilityList)
for cityNum, cityProb in self.TransferProbabilityList:
if threshold <= cityProb:
return (cityNum)
return None
def MoveToNextCity(self, alpha, beta):
'''
对于有0返回值的if语句不能使用if x: ... 判断
'''
nextCity = self.SelectNextCity(alpha, beta)
if nextCity is not None:
self.CurrCity = nextCity
self.TabuCityList.append(nextCity)
self.AllowedCitySet.remove(nextCity)
def UpdatePathLen(self):
for city, nextCity in zip(self.TabuCityList[:-1],
self.TabuCityList[1:]):
self.CurrLen = self.CurrLen + self.CityDistance[city][nextCity]
#~print(self.TabuCityList)
lastCity = self.TabuCityList[-1]
firstCity = self.TabuCityList[0]
self.CurrLen = self.CurrLen + self.CityDistance[lastCity][firstCity]
def two_opt_search(self):
'''
1-2-3-4, 1-2 + 3-4 > 1-3 + 2-4 则交换
'''
cityNum = len(self.TabuCityList)
for i in range(cityNum):
for j in range(cityNum - 1, i, -1):
curCity1 = self.TabuCityList[i]
preCity1 = self.TabuCityList[(i - 1) % cityNum]
curCity2 = self.TabuCityList[j]
nextCity2 = self.TabuCityList[(j + 1) % cityNum]
CurrLen = self.CityDistance[preCity1][
curCity1] + self.CityDistance[curCity2][nextCity2]
NextLen = self.CityDistance[preCity1][
curCity2] + self.CityDistance[curCity1][nextCity2]
if NextLen < CurrLen:
tempList = self.TabuCityList[i:j + 1]
self.TabuCityList[i:j + 1] = tempList[::-1]
if __name__ == '__main__':
aco = MMAS()
aco.ReadCityInfo('eil51.tsp')
aco.Search()
代码3
- 再略微修改,增加了邻近城市选择的机制,(详见文末资料)
# -*- coding: UTF-8 -*-
import random
from math import pow, sqrt
import numpy as np
import pandas as pd
import pylab as pl
class MMAS:
def __init__(self, antCount=20, q=100, alpha=1, beta=3,
rou=0.3, initialph=10, nMax=10000):
'''
https://svn-d1.mpi-inf.mpg.de/AG1/MultiCoreLab/papers/StuetzleHoos00%20-%20MMAS.pdf
'''
self.AntCount = antCount
self.Q = q
self.Alpha = alpha
self.Beta = beta
self.Rou = rou
self.initialPh = initialph
self.Nmax = nMax
self.Shortest = float('inf')
self.AntList = []
pl.show()
def ReadCityInfo(self, fileName):
'''
http://stackoverflow.com/questions/29281680/numpy-individual-element-access-slower-than-for-lists
'''
city_info = pd.read_csv(fileName,
sep=' ',
skiprows=6, skipfooter=1,
engine='python',
header=None,
names=('N', 'x', 'y'))
self.CityCount = city_info.shape[0]
self.CitySet = set()
self.CityDistance = np.zeros(
(self.CityCount, self.CityCount))
self.CityDistanceBeta = [
[0] * self.CityCount for i in range(self.CityCount)]
self.Pheromone = [
[self.initialPh] * self.CityCount for i in range(self.CityCount)]
self.PheromoneDelta = np.zeros(
(self.CityCount, self.CityCount)).tolist()
self.BestTour = [None] * self.CityCount
for row in city_info.index:
for col in city_info.index:
if row != col:
distance = round(
sqrt(pow(city_info.x[row] - city_info.x[col], 2)
+ pow(city_info.y[row] - city_info.y[col], 2))
)
self.CityDistance[row][col] = distance # 可用[row, col]索引
self.CityDistanceBeta[row][col] = pow(
1.0 / distance, self.Beta)
self.CityNearest = self.CityDistance.argsort() # 每个城市de最近城市索引
# http://stackoverflow.com/questions/7851077/how-to-return-index-of-a-sorted-list
self.CityDistance = self.CityDistance.tolist()
self.city_info = city_info
def PutAnts(self):
self.AntList.clear()
for antNum in range(self.AntCount):
city = random.choice(self.city_info.index)
ant = ANT(city, self.city_info.index,
self.CityDistance, self.Pheromone,
self.CityNearest)
self.AntList.append(ant)
def Search(self):
import time
for iter in range(self.Nmax):
start = time.time()
self.PutAnts()
tmpLen = float('inf')
tmpTour = []
for ant in self.AntList:
for ttt in range(self.CityCount):
ant.MoveToNextCity(self.Alpha, self.Beta)
ant.two_opt_search()
ant.UpdatePathLen()
if ant.CurrLen < tmpLen:
self.bestAnt = ant
tmpLen = ant.CurrLen
tmpTour = ant.TabuCityList
if tmpLen < self.Shortest:
self.Shortest = tmpLen
self.BestTour = tmpTour
print(iter, "-->", self.Shortest, "-->", self.BestTour)
# self.bestAnt.two_opt_search()
self.UpdatePheromoneTrail()
end = time.time()
print(end - start)
pl.clf()
x = []
y = []
for city in self.BestTour:
x.append(self.city_info.x[city])
y.append(self.city_info.y[city])
x.append(x[0])
y.append(y[0])
pl.plot(x, y)
pl.scatter(x, y, s=30, c='r')
pl.pause(0.01)
def UpdatePheromoneTrail(self):
ant = self.bestAnt
pheromo_new = self.Q / ant.CurrLen
tabu = ant.TabuCityList
PD = self.PheromoneDelta
P = self.Pheromone
citys = self.city_info.index
for city, nextCity in zip(tabu[:-1], tabu[1:]):
PD[city][nextCity] = pheromo_new
PD[nextCity][city] = pheromo_new
lastCity = tabu[-1]
firstCity = tabu[0]
PD[lastCity][firstCity] = pheromo_new
PD[firstCity][lastCity] = pheromo_new
for c1 in citys:
for c2 in citys:
if c1 != c2:
P[c1][c2] = (
(1 - self.Rou) * P[c1][c2]
+ PD[c1][c2]
)
if P[c1][c2] < 0.001:
P[c1][c2] = 0.001
if P[c1][c2] > 10:
raise(Exception('too big Ph'))
P[c1][c2] = 10
PD[c1][c2] = 0
class ANT:
def __init__(self, currCity=0, citys=None,
cityDis=None, pheromo=None, cityNear=None):
self.TabuCityList = [currCity, ]
self.AllowedCitySet = set(citys)
self.AllowedCitySet.remove(currCity)
self.CityDistance = cityDis
self.Pheromone = pheromo
self.CityNearest = cityNear
self.TransferProbabilityList = []
self.CurrCity = currCity
self.CurrLen = 0
def SelectNextCity(self, alpha, beta):
if len(self.AllowedCitySet) == 0:
return None
near = self.CityNearest[self.CurrCity]
ANset = self.AllowedCitySet & set(near[1:16])
if ANset:
sumProbability = 0
self.TransferProbabilityList = []
for city in self.AllowedCitySet:
sumProbability = sumProbability + (
pow(self.Pheromone[self.CurrCity][city], alpha) *
pow(1.0 /
self.CityDistance[self.CurrCity][city], beta)
)
transferProbability = sumProbability
self.TransferProbabilityList.append(
(city, transferProbability))
threshold = sumProbability * random.random()
for cityNum, cityProb in self.TransferProbabilityList:
if threshold <= cityProb:
return (cityNum)
else:
for city in near[1:]:
if city in self.AllowedCitySet:
return city
def MoveToNextCity(self, alpha, beta):
'''
对于有0返回值的if语句不能使用if x: ... 判断
'''
nextCity = self.SelectNextCity(alpha, beta)
if nextCity is not None:
self.CurrCity = nextCity
self.TabuCityList.append(nextCity)
self.AllowedCitySet.remove(nextCity)
def UpdatePathLen(self):
for city, nextCity in zip(self.TabuCityList[:-1],
self.TabuCityList[1:]):
self.CurrLen = self.CurrLen + self.CityDistance[city][nextCity]
#~print(self.TabuCityList)
lastCity = self.TabuCityList[-1]
firstCity = self.TabuCityList[0]
self.CurrLen = self.CurrLen + self.CityDistance[lastCity][firstCity]
def two_opt_search(self):
'''
1-2-3-4, 1-2 + 3-4 > 1-3 + 2-4 则交换
'''
cityNum = len(self.TabuCityList)
for i in range(cityNum):
for j in range(cityNum - 1, i, -1):
curCity1 = self.TabuCityList[i]
preCity1 = self.TabuCityList[(i - 1) % cityNum]
curCity2 = self.TabuCityList[j]
nextCity2 = self.TabuCityList[(j + 1) % cityNum]
CurrLen = self.CityDistance[preCity1][
curCity1] + self.CityDistance[curCity2][nextCity2]
NextLen = self.CityDistance[preCity1][
curCity2] + self.CityDistance[curCity1][nextCity2]
if NextLen < CurrLen:
tempList = self.TabuCityList[i:j + 1]
self.TabuCityList[i:j + 1] = tempList[::-1]
if __name__ == '__main__':
aco = MMAS()
aco.ReadCityInfo('eil51.tsp')
aco.Search()
资料
- 以前在论坛上搜集的资料,讲得很好,现在暂时没找到出处,见谅。
这位同学的附件不错,说的很详细,是一个很好的入门教程
不过不够深入,而且有些地方明显是抄的其它中文资源
比如对MMAS的论述有很多错误,只是列举一串公式没有提到具体实现,凡是这样的文章通常都是作者自己没学会含糊其辞,要么就是直接抄的
附件应该是抄的,因为 avg 参数的论述完全错误,可见作者根本没有写过MMAS,或者写过但是不会有他声称的增强
(如果同学看中文资料看不懂,很正常,因为很可能是错的。。。。。。)
其实《Ant Colony Optimization》一书就有MMAS详细的实现方法和参数建议。
我现在看到拿 eil51.tsp 作为最终考验,或者求解规模在100以下的,都觉得作者水平低+多半是抄书郎了,因为只要自己看过《Ant Colony Optimization》,都绝对不止求解100规模的实力。
因为只要有了邻域搜索,求解数百城市都不成问题,根据我的经验,
没有邻域搜索的,100城市以上几乎是绝对求不出最优解,所以100城市是个分水岭(我现在无视这个水平)
2_opt在求解300+的城市会出现明显精度下降,所以300城市规模也是一个分水岭(我现在轻视这个水平)
3_opt在求解1000+的城市会出现明显精度下降,所以1000城市规模也是一个分水岭(我现在站在这个水平)
LKH我没学习,据作者说可以直接优化10万城市!!!所以。。。10万城市也是一个分水岭(我现在仰望这个水平)
再次推书:《Ant Colony Optimization》一书里面的内容是很多的,至少还有:
1 各种蚁群算法的详细实现,及其性能比较(我在顶楼贴了性能比较和建议参数这非常重要的两页资料,很多资料都直接引用这两页而不提出处,鄙视。)
2 对算法陷入停滞的检测方法(绝绝大多数网上资源根本不提这一点,或者提到了也是错的,如楼上中原小农的附件,里面说到轮盘赌选择是避免停滞,这一句就是错误的,轮盘赌选择是最基本的蚁群算法的核心实现,目的只是每个路径都有机会被搜索到,跟避免算法停滞没有半点关系。)
3 对算法的加速技巧(应用加速技巧,可以把蚁群算法降低一个阶,变成 O(n^2) 提速几千倍!)
4 更高级的邻域搜索,如 3_opt,k_opt,LKH,绝大多数网上资源根本不提邻域搜索,所以性能一般都很差。
有能力的同学绝对应该直接看《Ant Colony Optimization》,看完就知道所有中文资源都是二手货+太监版(包括我的,呵呵)。
前面说到,蚁群算法 + 邻域搜索 = 很好的优化程度
但是,我们发现求解超过200城市规模的TSP问题,还是显得太慢。
在进一步深入优化蚁群算法之前,显然必须先解决速度太慢的问题。
原有的蚁群算法的性能分析如下:
算法复杂度 = O( 循环数 * 蚂蚁数 * 城市数^2 )
在没有邻域搜索辅助的情况下,设城市数 = N
循环数通常需要指定一个很大的数值,假设这个值为T
而蚂蚁数的取值,建议=城市数,所以每次循环计算所有蚂蚁需要 O(N)
一个蚂蚁的一个方案需要选择N个城市,每次选择需要从 最多N个候选城市中遍历并且计算选择概率,所以建立一个方案是 O(N^2)
所以算法的复杂度 = T * N^3,即 O(T * N^3)
这样的算法复杂度意味着,如果求解10个城市需要0.01秒,那么
求解150个城市就需要 15^3 * 0.01 = 33.75秒!
求解300个城市就需要 30^3 * 0.01 = 270秒!
求解1000个城市就需要 100^3 * 0.01 = 1万秒!
程序耗时随着城市数增大,呈现3次方增长,这显然是无法求解更大规模的问题的。
在使用了邻域搜索以后,我们发现可以大大减少需要的循环数,即T可以降低,但即使忽略不计T这个值,程序仍然是 O(N^3)增长速度,一切还是不变。
采用以下三个技巧,可以把 算法复杂度降低到 O(T * N^2)
头两个加速技巧都基于一个事实: TSP问题最优解的每个城市连接的都必定是附近的城市!
所以在蚂蚁寻路的时候,也只需要尝试附近的几个城市即可,不需要尝试所有的城市!
技巧1 : candidate list,或者说 Nearest city list
即每个蚂蚁在计算如何选择下一个城市时,只计算距离当前城市距离最近的若干个城市,如果这些距离最近的城市已经走过,那么就放弃蚁群算法的概率选择路径,直接用贪婪法选择可用的最近城市
当然,我们需要预先建立一个“优先城市”的矩阵,以方便查找。
技巧2 :Fixed radius search
即在邻域搜索的时候,也不需要尝试一个城市跟所有其他城市的连接能否交换出更好的结果,只需要尝试跟最靠近的若干个城市的交换
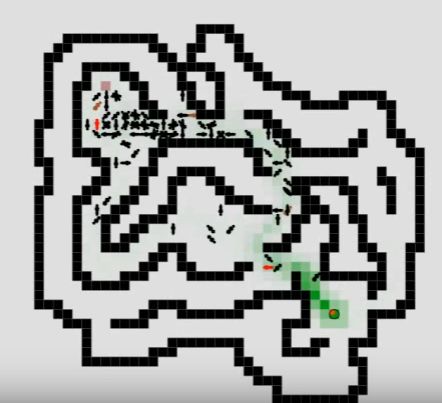
这两个技巧可以把之前的尝试N个城市,变为尝试指定范围n (n相关演示视频
- Ant Colony Optimization (AntSIm v1.1) Find an optimal path in labyrinth
- Ant Algorithm Simulator
- Ant Colony Optimization and Genetic Algorithms for the TSP
- Ant Colony Optimization Simulation
- Ant Colony Optimization (AntSIm v1.1)
其他资料下载
链接:http://pan.baidu.com/s/1o7KTaiu 密码:sv1s