WaitFoF

图像透视变换应用

简介

透视变换是将成像投影到一个新的视平面，也称作投影映射。投影变换是三维空间上的非线性变换，可看做是仿射变换的更一般形式，简单讲即通过一个3x3的变换矩阵将原图投影到一个新的视平面(Viewing Plane)，在视觉上的直观表现就是产生或消除了远近感。

OpenCV透视变换的透视变换

1、warpPerspective

利用透视矩阵对图像进行透视变换。

说明
OpenCV提供了warpPerspective( )函数来实现图片的透视变换，只需要输入梯形四个顶点的坐标和目标画布四个角的坐标，即可自动完成转换。核心代码只有两行：首先读取两个坐标数组，计算变换矩阵；然后根据变换矩阵对原图进行透视变换，并输出到目标画布。

函数warpPerspective使用指定的矩阵转换源图像：
$\texttt{dst} (x,y) = \texttt{src} \left ( \frac{M_{11} x + M_{12} y + M_{13}}{M_{31} x + M_{32} y + M_{33}} , \frac{M_{21} x + M_{22} y + M_{23}}{M_{31} x + M_{32} y + M_{33}} \right )$
当设置标志WARP_INVERSE_MAP时。否则，首先使用invert反转转换，然后将其放在上面的公式中，而不是M中。

声明

void warpPerspective(
		InputArray src,
		OutputArray dst,
		InputArray M,
		Size dsize,
		int flags=INTER_LINEAR,
		int borderMode= BORDER_CONSTANT,
		const Scalar &borderValue=Scalar() 
)

参数

src	输入图像
dst	输出图像，其大小为dsize，并且类型与src相同。
M	3×3的转换矩阵。
dsize	输出图像的尺寸大小。
flags	插值方法(INTER_LINEAR或INTER_NEAREST)与可选标志WARP_INVERSE_MAP的组合，设置M为逆变换（ $\texttt{dst}\rightarrow\texttt{src}$ ）。
borderMode	边界补偿方式,BORDER_CONSTANT 或者BORDER_REPLICATE
borderValue	边界补偿大小，常值，默认为0。

关于变换矩阵M，OpenCV提供两种方法计算：

1.1、findHomography–计算透视矩阵

通过输入和输出图像中两组点计算透视矩阵。

说明
查找两个平面之间的透视转换。
通过变换前、后两个平面的点寻找出一个单应性变换矩阵H:

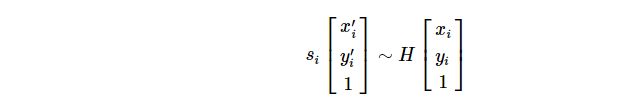
使得反投影误差：
$\sum _i \left ( x'_i- \frac{h_{11} x_i + h_{12} y_i + h_{13}}{h_{31} x_i + h_{32} y_i + h_{33}} \right )^2+ \left ( y'_i- \frac{h_{21} x_i + h_{22} y_i + h_{23}}{h_{31} x_i + h_{32} y_i + h_{33}} \right )^2$ 被最小化。

如果参数方法设置为默认值0，则该函数使用所有点对通过简单的最小二乘方案计算初始单应性估计。

但是，如果不是所有的点对（ $srcPoints_i$ , $dstPoints_i$ )都适合严格的透视图转换(也就是说，存在一些异常值)，那么这个初始估计就会很差。在这种情况下，您可以使用三种健壮方法中的一种。RANSAC方法,LMeDS和 RHO尝试许多不同的随机对应点对的子集(四双,共线双被丢弃),估计单应性矩阵使用这个子集和一个简单的最小二乘算法,然后计算计算单应性的质量/善良的数量(这是内围层RANSAC或至少值重新投影误差LMeDS)。然后使用最佳子集生成单应矩阵的初始估计inliers/outliers的掩码。

无论采用何种方法，无论是否健壮，都可以使用Levenberg-Marquardt方法进一步精简计算出的单应性矩阵（仅在稳健方法中使用inliers），以进一步降低重投影误差。

RANSAC和RHO的方法几乎可以处理任何异常值比率，但是需要一个阈值来区分异常值和异常值。LMeDS方法不需要任何阈值，但是只有在有超过50％的内部值时，它才能正确运行。最后，如果没有异常值并且噪声很小，请使用默认方法（method= 0）。

声明

Mat findHomography( 
     InputArray srcPoints, 
     InputArray dstPoints,
     int method = 0, 
     double ransacReprojThreshold = 3,
     OutputArray mask=noArray(), 
     const int maxIters = 2000,
     const double confidence = 0.995
);

Mat findHomography(
    InputArray srcPoints, 
    InputArray dstPoints,
    OutputArray mask, 
    int method = 0, 
    double ransacReprojThreshold =3
);

参数

srcPoint	原始平面中点的坐标，其类型为CV_32FC2或vector 的矩阵。
dstPoint	目标平面中点的坐标，类型为CV_32FC2的矩阵或vector 。
method	用于计算单应矩阵的方法。
ransacReprojThreshold
mask	通过可靠的方法(RANSAC或LMEDS）设置的可选输出掩码。请注意，输入掩码值将被忽略。
maxIters	RANSAC的最大迭代次数。
confidence	置信度，介于0和1之间。

method取值

0: 使用所有点的常规方法，即最小二乘法

RANSAC: 基于RANSAC的鲁棒方法

LMEDS: 最小中值稳健方法

RHO: 基于PROSAC稳健的方法

1.2、getPerspectiveTransform–根据四对对应点计算透视变换

通过原图和变换后图像的4个对应点(即对应的四边形)计算出透视变换矩阵。

说明
The function calculates the 3×3 matrix of a perspective transform so that:

声明

Mat cv::getPerspectiveTransform	(	    
        InputArray 	src,
		InputArray 	dst,
		int solveMethod = DECOMP_LU 
)	

Mat cv::getPerspectiveTransform	(	
		const Point2f 	src[],
		const Point2f 	dst[],
		int 	solveMethod = DECOMP_LU 
)

参数

src	源图像中四边形顶点的坐标。
dst	目标图像中相应四边形顶点的坐标。
solveMethod	传递给cv :: solve（DecompTypes）的方法。

2、perspectiveTransform–点的透视变换

利用透视矩阵对点进行透视变换。

说明
执行向量的透视矩阵转换。

函数cv :: perspectiveTransform通过将src的每个元素视为2D或3D向量来对其进行转换，其方式如下：

这里显示了3D矢量变换。在2D矢量变换的情况下，将省略z分量。

该函数转换2D或3D向量的稀疏集合。如果要使用透视变换来变换图像，请使用warpPerspective。如果存在反问题，也就是说，您想从几对对应点中计算出最可能的透视变换，则可以使用getPerspectiveTransform或findHomography。

声明

void perspectiveTransform(	   
    InputArray src,
    OutputArray dst,
    InputArray m 
)

参数

src	输入两通道或三通道浮点数组；每个元素都是要转换的2D / 3D向量。
dst	与src具有相同大小和类型的输出数组。
m	3x3或4x4浮点转换矩阵。

应用

❶简单变换

void onMouse(int event, int x, int y, int flags, void* utsc) {
     
	if (event==EVENT_LBUTTONUP)
	{
     
		//画出源图像中需要透视到四边形中的4个待转换点
		circle(src2, Point(x, y), 2, Scalar(0, 0, 255), 2);
		imshow("wait", src2);
		//记录原图中待转换的点坐标
		srcTri[clickTimes].x = x;
		srcTri[clickTimes].y = y;
		clickTimes++;
		cout << "The" << clickTimes << " point: [ " << srcTri[clickTimes - 1].x << "," << srcTri[clickTimes - 1].y << "]" << endl;
	}
	if (clickTimes == 4) {
     

		//将原图像中的四个点转换到目的图形的对应四个点上
		//第一个点——左上角
		dstTri[0].x = 0;
		dstTri[0].y = 0;
		//第二个点——右上角
		dstTri[1].x = 480;
		dstTri[1].y = 0;
		//第三个点——右下角
		dstTri[2].x = 480;
		dstTri[2].y = 600;
		//第四个点——左下角
		dstTri[3].x = 0;
		dstTri[3].y = 600;

		//通过原图像和目标图像中4个对应点求出透视矩阵
		Mat m = findHomography(srcTri, dstTri, RANSAC);
		warpPerspective(src, dst, m, Size(480, 600));
		imshow("dst", dst);
	}
}

int main() {
     
	src = imread("D:/test/m.png");
	src2 = src.clone();
	namedWindow("src", WINDOW_AUTOSIZE);
	imshow("src", src2);
	setMouseCallback("src", onMouse);


	waitKey(0);
	return 0;
}

注意：需要注意透视变换中点与点的对应顺序，应该顺时针方向进行点的转换。

❷复杂的透视变换
可以结合第一个应用的方式，使用点击事件进行获取需要在目标图片上转换的具体坐标。

void warpPerspectiveTest() {
     
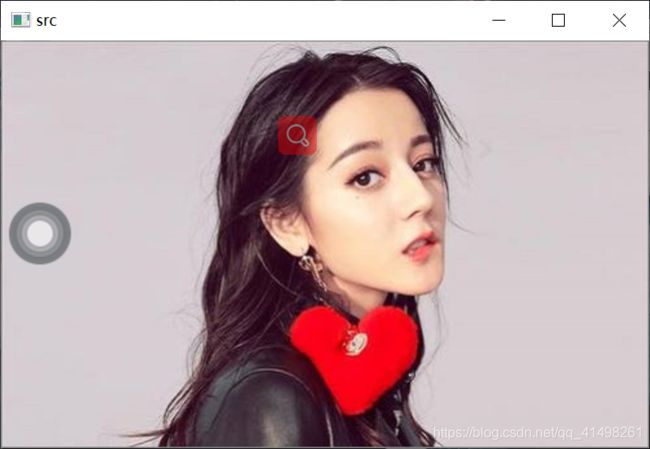
    //1 读取广告图
	Mat src = imread("D:/test/src.jpg");
	imshow("src", src);
   
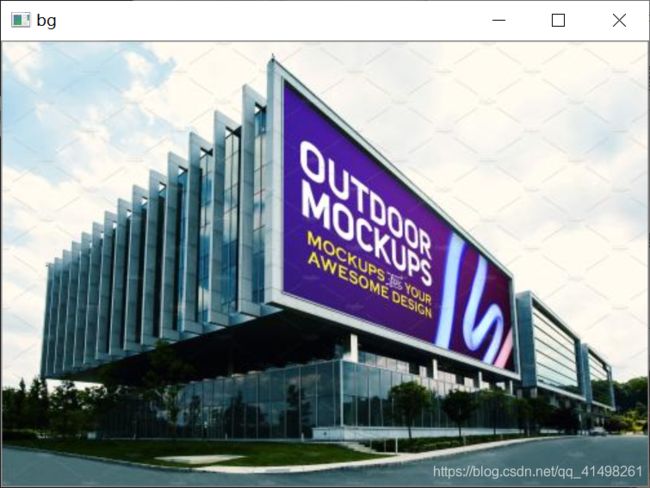
    //2 读取广告牌背景图
	Mat bg = imread("D:/test/bg.jpg");
	Mat bg_temp = bg.clone();
	imshow("bg", bg);

	
	//3 透视变换4对坐标确定
	vector<Point2f> srcTri(4), dstTri(4);
	//3.1 源图的四个坐标
	srcTri[0].x = 0;
	srcTri[0].y = 0;
	srcTri[1].x = src.cols-1;
	srcTri[1].y = 0;
	srcTri[2].x = src.cols-1;
	srcTri[2].y = src.rows-1;
	srcTri[3].x = 0;
	srcTri[3].y = src.rows-1;

	//3.2 目标图片的四个坐标
	//用画图工具测试的4个点的像素坐标
	dstTri[0].x = 218;
	dstTri[0].y = 31;
	dstTri[1].x = 392;
	dstTri[1].y = 182;
	dstTri[2].x = 399;
	dstTri[2].y = 258;
	dstTri[3].x = 218;
	dstTri[3].y = 194;
	

	//4 求出透视变换的矩阵
	//Mat m=getPerspectiveTransform(srcTri, dstTri);
	Mat m = findHomography(srcTri, dstTri);
	//5 进行透视变换
	warpPerspective(src, bg_temp, m, bg.size());
	imshow("bg_temp", bg_temp);

	//fillConvexPoly(InputOutputArray img, const Point * pts, int npts,
	//	const Scalar & color, int lineType = LINE_8,
	//	int shift = 0);
	Point pt[4];
	for (size_t i = 0; i < 4; i++)
	{
     
		pt[i] = dstTri[i];
	}
	//6 在目标图像中去除多边形区域，并合并
	fillConvexPoly(bg, pt, 4,Scalar(0));
	Mat dst;
	add(bg,bg_temp , dst);
	imshow("dst", dst);
}

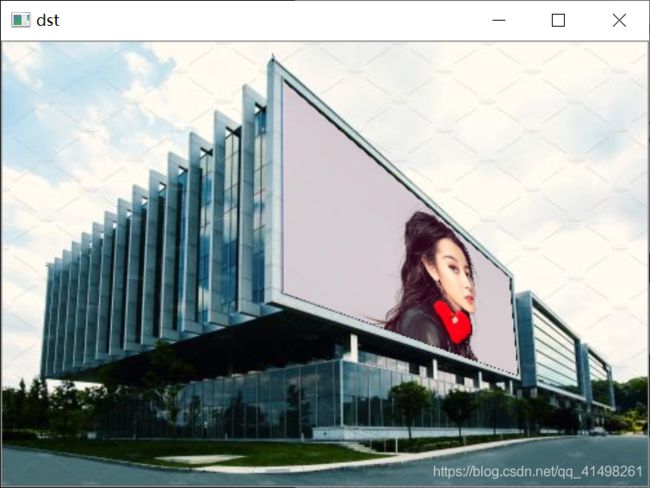
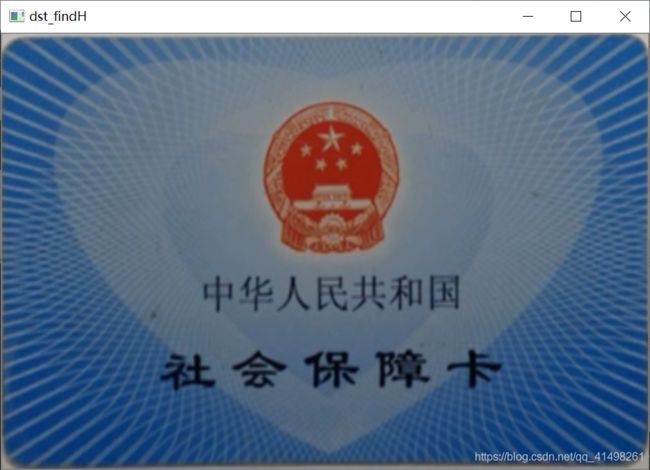
❸自动检测源映射坐标
上面都是手动或者自己输入的变换源坐标，下面让计算机自己检测需要的4个坐标。
步骤：

图片预处理
1.1 灰度
1.2 二值化分割
1.3 去噪声
1.4 闭操作
寻找轮廓
霍夫直线检测
定位边沿轮廓直线
直线方程
直线交点
透视矩阵
透视变换

void  warpPerspectiveTest2() {
     
   Mat src = imread("D:/test/kak.png");
   imshow("src", src);
   //1. 图片预处理
   //1.1 灰度化
   Mat gray_src;
   cvtColor(src, gray_src, COLOR_BGR2GRAY);
   //1.2 去噪声
   blur(gray_src, gray_src, Size(3, 3));

   //1.3 二值化
   Mat binary_src;
   threshold(gray_src, binary_src, 0, 255, THRESH_BINARY_INV|THRESH_OTSU);
   imshow("binary_src", binary_src);


   //1.4 闭操作
   Mat closed_src;
   Mat kernel = getStructuringElement(MORPH_RECT, Size(3, 3));
   morphologyEx(binary_src, closed_src, MORPH_CLOSE,kernel );
   imshow("closed_src", closed_src);

   //2. 寻找轮廓
   vector<vector<Point>> contours;
   Mat draw = Mat::zeros(src.size(), src.type());
   //注意寻找轮廓的方法，只寻找最外围的轮廓
   findContours(closed_src, contours, RETR_EXTERNAL, CHAIN_APPROX_SIMPLE);
   //2.1 遍历每一个轮廓
   for (size_t i = 0; i < contours.size(); i++)
   {
     
   	Rect rect = boundingRect(contours[i]);
   	if (rect.width < src.cols / 2 && rect.height < src.rows / 2)
   		continue;
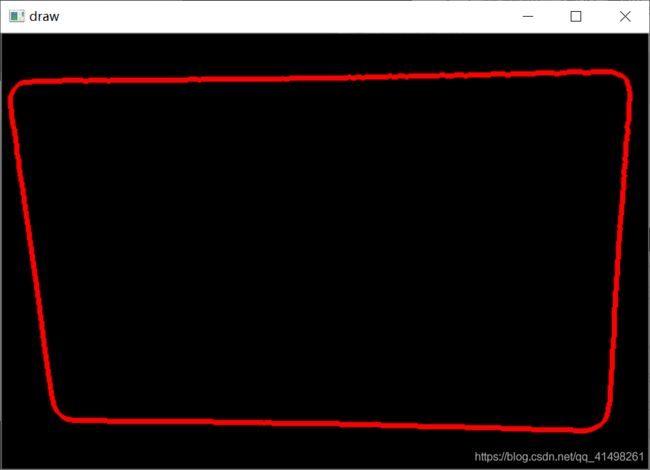
   	//2.2 画出筛选后的轮廓
   	drawContours(draw, contours, i, Scalar(0, 0, 255),3);
   }
   imshow("draw", draw);
   
   //3. 霍夫直线检测--为了匹配四个边
   vector<Vec4i> lines;
   cvtColor(draw, draw, COLOR_BGR2GRAY);
   //Each line is represented by a 4-element vector，(x1, y1, x2, y2), where (x1,y1)and(x2, y2)are the ending points of each detected
   //3.1 找出所有的直线
   HoughLinesP(draw, lines, 1, CV_PI / 180, src.rows / 2, src.rows / 2, 0);
   Mat draw2 = Mat::zeros(src.size(), src.type());
   for (int j = 0; j < lines.size(); j++) {
     
   	Vec4i ln = lines[j];
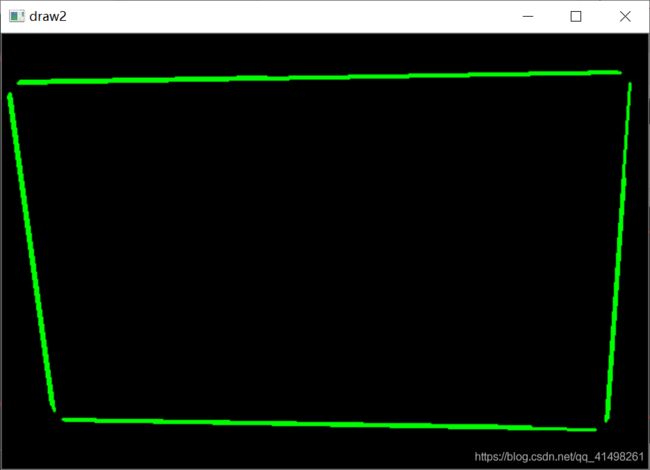
   	//3.2 画出所有的直线
   	line(draw2, Point(ln[0], ln[1]), Point(ln[2], ln[3]), Scalar(0, 255, 0), 2);
   }
   cout << "lines.size=" << lines.size() << endl;
   imshow("draw2", draw2);
   
   //4. 定位边沿轮廓直线
   Vec4i topLine, bottomLine, leftLine, rightLine;
   for (size_t i = 0; i < lines.size(); i++)
   {
     
   	Vec4i ln = lines[i];
   	//4.1找最左侧的直线，确定左侧直线的两个点的横坐标在图像中心的左侧区域
   	if (ln[0] < src.cols / 2 && ln[2] < src.cols / 2) {
     
   		leftLine = ln;
   	}
   	//4.2找顶部的直线，确定顶部直线的两个点的纵坐标在图像中心的上方区域内
   	if (ln[1] < src.rows / 2 && ln[3] < src.rows / 2) {
     
   		topLine = ln;
   	}
   	//4.3找最右侧的直线，确定右侧直线的两个点的横坐标在图像中心的右侧区域
   	if (ln[0] > src.cols / 2 && ln[2] > src.cols / 2) {
     
   		rightLine = ln;
   	}
   	//4.4找底部的直线，确定底部直线的两个点的纵坐标在图像中心的下方区域内
   	if (ln[1] > src.rows / 2 && ln[3] > src.rows / 2) {
     
   		bottomLine = ln;
   	}
   }
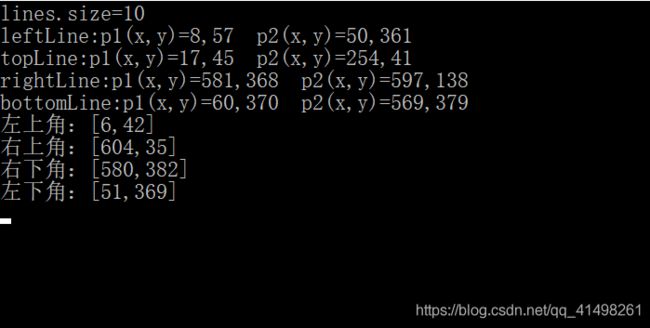
   cout << "leftLine:p1(x,y)=" << leftLine[0] << "," << leftLine[1] << "  " << "p2(x,y)=" << leftLine[2] << "," << leftLine[3] << endl;
   cout << "topLine:p1(x,y)=" << topLine[0] << "," << topLine[1] << "  " << "p2(x,y)=" << topLine[2] << "," << topLine[3] << endl;
   cout << "rightLine:p1(x,y)=" << rightLine[0] << "," << rightLine[1] << "  " << "p2(x,y)=" << rightLine[2] << "," << rightLine[3] << endl;
   cout << "bottomLine:p1(x,y)=" << bottomLine[0] << "," << bottomLine[1] << "  " << "p2(x,y)=" << bottomLine[2] << "," << bottomLine[3] << endl;
   
   //5. 直线方程
   //5.1求出左侧直线的方程 y=kx+b:  k=(y2-y1)/(x2-x1)  b=y-kx 
   double kl = double(leftLine[3] - leftLine[1]) / double(leftLine[2] - leftLine[0]);
   double bl = double(leftLine[1] - kl * leftLine[0]);
   //5.2求出顶侧直线的方程 
   double kt = double(topLine[3] - topLine[1]) / double(topLine[2] - topLine[0]);
   double bt = double(topLine[1] - kt * topLine[0]);
   //5.3求出右侧直线的方程 
   double kr = double(rightLine[3] - rightLine[1]) / double(rightLine[2] - rightLine[0]);
   double br = double(rightLine[1] - kr * rightLine[0]);
   //5.4求出底部直线的方程  
   double kb = double(bottomLine[3] - bottomLine[1]) / double(bottomLine[2] - bottomLine[0]);
   double bb = double(bottomLine[1] - kb * bottomLine[0]);

   //6. 直线交点
   Point p1, p2, p3, p4;
   //6.1左侧直线和顶部直线的交点: x=(b2-b1)/(k1-k2)  y=k1*x+b1
   p1.x = int((bt - bl) / (kl - kt));
   p1.y = int(kl * p1.x + bl);
   //6.2顶部直线和右侧直线的交点
   p2.x = int((br - bt) / (kt - kr));
   p2.y = int(kt * p2.x + bt);
   //6.3右侧直线和底部直线的交点
   p3.x = int((bb - br) / (kr - kb));
   p3.y = int(kr * p3.x + br);
   //6.4底部直线和左侧直线的交点
   p4.x = int((bl - bb) / (kb - kl));
   p4.y = int(kb * p4.x + bb);
   cout << "左上角：[" << p1.x << "," << p1.y <<"]"<< endl;
   cout << "右上角：[" << p2.x << "," << p2.y <<"]"<< endl;
   cout << "右下角：[" << p3.x << "," << p3.y <<"]"<< endl;
   cout << "左下角：[" << p4.x << "," << p4.y <<"]"<< endl;
   //6.5画出交点
   circle(draw2, p1, 2, Scalar(0, 0, 255));
   circle(draw2, p2, 2, Scalar(0, 0, 255));
   circle(draw2, p3, 2, Scalar(0, 0, 255));
   circle(draw2, p4, 2, Scalar(0, 0, 255));
   imshow("draw2-point", draw2);

   //7. 透视矩阵  
   //将检测出来的4个点变换到新的对应的4个点坐标
   //7.1源图像的四个待映射的点
   vector<Point2f> srcTri(4);
   srcTri[0] = p1;
   srcTri[1] = p2;
   srcTri[2] = p3;
   srcTri[3] = p4;
   //7.2目标图像中相对应的点
   vector<Point2f> dstTri(4);
   dstTri[0] = Point(0, 0);
   dstTri[1] = Point(src.cols, 0);
   dstTri[2] = Point(src.cols, src.rows);
   dstTri[3] = Point(0, src.rows);
   //7.3获取透视变换的矩阵
   Mat m_FindH=findHomography(srcTri, dstTri);
   Mat m_getPT=getPerspectiveTransform(srcTri, dstTri);

   //8 透视变换
   Mat dst_findH = Mat::zeros(src.size(), src.type());
   Mat dst_getPT = Mat::zeros(src.size(), src.type());
   warpPerspective(src, dst_findH, m_FindH, src.size());
   warpPerspective(src, dst_getPT, m_FindH, src.size());

   imshow("dst_findH", dst_findH);
   imshow("dst_getPT", dst_getPT);
   
}

学习：
【OpenCV3.3】通过透视变换矫正变形图像

Opencv日常之Homography

【OpenCV】透视变换 Perspective Transformation（续）

【图像处理】透视变换 Perspective Transformation

图像透视变换原理及实现

详解 OpenCV 透视变换原理及实例