学习了「数据预处理」之后,让我们一起来实现第一个预测模型——简单线性回归模型。
一、理解原理
简单线性回归是我们接触最早,最常见的统计学分析模型之一。
假定自变量 与因变量 线性相关,我们可以根据一系列已知的 数据,通过某种方法,拟合出一条直线 ,并利用这条直线预测 的值 。这种方法就叫作简单线性回归。
那么我们该如何去拟合出这条直线,才能使预测的结果最准确呢?
常用的方法是最小二乘法。
最小二乘法
课本上关于最小二乘法的概念困扰了我许久,后来无意中看到了它的英文——
Least Squares Method(LSM),平方...二乘...嗯,没毛病。
沿用这个名称可以理解,算是一种情怀或是传承,但是我想说一个事物的名称真的很重要,一个不恰当的名字会徒增很多理解上的负担。(比如区块链,取这么个名字就没想让一般群众理解,我第一次看见这个名字时的感觉就是不知所云)
不吐槽了,最小二乘法,或者按我的翻译——平方和最小法,就是使得我们通过观测得到的,已知的 值与通过线性模型预测得到的 之间的差值的平方之和
最小。可以看做是 与 之间的距离之和。以 最小作为评判依据显然是比较科学的。
根据这个条件,我们可以求出直线的截距 和斜率 ,得到我们所需的线性模型。对求解过程有兴趣的同学可以参考 CSDN - 普通最小二乘法的推导证明,当然,对 Python 来说,我们可以不关注具体实现的方式而直接去利用封装好的模型。时间和精力有限的同学跟着往下走就好。
梯度下降法 *
考虑到计算机能够进行大量重复计算,实际上我们通常使用迭代的方法来求得参数。所谓迭代,即按照一定的步长逐个取参数值,并按某种原则(如最小二乘)评估用这些值进行拟合的合理性,最终选取最合适的参数值。
梯度下降法是一种常见的迭代方法,解决了当有多个自变量(特征)时往什么方向(选取什么方向的特征向量)迭代能够使函数值最终收敛到最小值的问题。
实际上,在输入特征较多的情况下,使用迭代法所需的计算量将远远小于解析法。
关于如何理解梯度下降法及其数学原理,参见我的文章「如何理解梯度下降法」。
二、代码实现
之前,我们搭建好了进行数据分析所需的 Python 环境(还没有搭建好的同学可以参考我的文章「机器学习入坑指南(一):Python 环境搭建」), 接下来,我们将实现简单线性回归模型。 建议大家和我一样使用 Jupyter Notebook,在后面你会更深刻地感受到它的魅力。
1 数据预处理
第一步当然就是上一篇文章讲解的数据预处理啦,代码如下:
# 导入需要的库
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# 读取数据
dataset = pd.read_csv('studentscores.csv')
X = dataset.iloc[ : , : 1 ].values
Y = dataset.iloc[ : , 1 ].values
# 分割数据
from sklearn.cross_validation import train_test_split
X_train, X_test, Y_train, Y_test = train_test_split( X, Y, test_size = 1/4, random_state = 0)
示例数据地址:GitHub - Avik-Jain/100-Days-Of-ML-Code/datasets
对这个过程不熟悉的,参考「机器学习入坑指南(二):数据预处理」
2 用训练集拟合简单线性回归模型
sklearn 库为我们提供了许多常用的数学模型,极大地简化了我们进行数据分析的步骤。我们首先导入线性回归模型:
from sklearn.linear_model import LinearRegression
然后,用训练集的数据去训练(拟合)模型
regressor = LinearRegression()
regressor = regressor.fit(X_train, Y_train)
经过训练后,regressor 便得到了拟合的结果,也就是直线的斜率和截距。
3 预测结果
接下来,我们使用拟合完的模型,根据测试集中的 X 值得到预测的 Y 值,这一步也非常简洁:
Y_pred = regressor.predict(X_test)
4 可视化
为了直观地表达模型拟合的效果,我们对上面的数据分析结果进行可视化。
还记得第一步中我们导入的 matplotlib.pyplot 吗?这是专门提供可视化的一个模块,提供了 Matlab 风格的编程接口(呃,我并不擅长 Matlab)。
这里我们使用它提供的两个方法,一个是 scatter,用来画点,另一个是 plot ,用来画线。当然这只是简单的用法,想进一步了解,参考 gitbooks - Pyplot 教程 。
训练集可视化
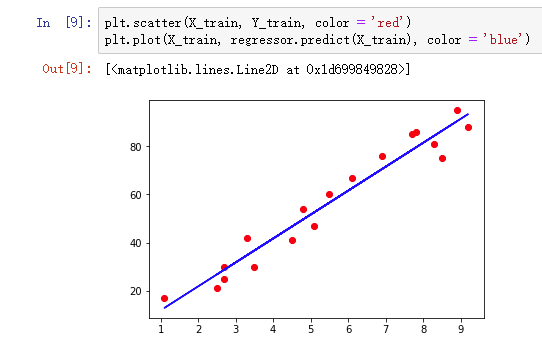
# 绘出数据点,用红色表示
plt.scatter(X_train , Y_train, color = 'red')
# 绘出拟合的直线,用蓝色表示
plt.plot(X_train , regressor.predict(X_train), color ='blue')
plt.show()
在 Jupyter Notebook 中输入上面的代码,可视化的结果如图
测试集可视化
同理,可视化测试集,输入以下代码
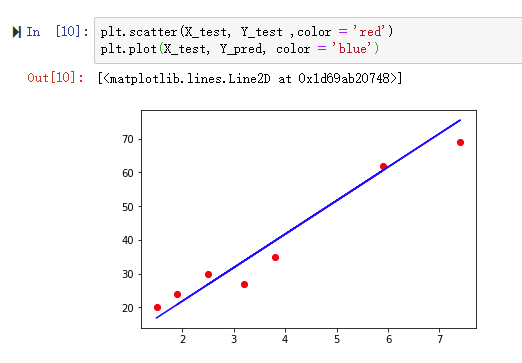
plt.scatter(X_test , Y_test, color = 'red')
plt.plot(X_test , regressor.predict(X_test), color ='blue')
plt.show()
结果如图
注意虽然绘制直线时使用的参数不一样,但直线是同一条直线,只是选取了不同的点。可以看出,预测的结果与实际的结果具有一定的一致性。
简单线性回归适用于使用一元特征来预测数值的情形。在下一篇文章里,我们将讨论多元线性回归。
欢迎关注 Evan 的博客