论文阅读《STEm-Seg: Spatio-temporal Embeddings for Instance Segmentation in Videos》
论文链接:https://arxiv.org/abs/2003.08429
STEmSeg是ECCV20上的一篇文章,做的是Video Instance Segmentation(VIS),提出了一种可以end-to-end的方法,大大简化了VIS的pipeline,同时在很多数据集上达到了SOTA。
过去很多经典的方法都遵循top-down模式,即仿照MOT里的tracking-by-detection的范式。这类方法通常会利用多个模型,先做单张image的检测,再做帧之间的association,对于occlusion用appearance model处理。这种pipeline虽然精度较高,但包含了太多的network,因此计算复杂,且无法end-to-end。
所以作者另辟蹊径,受Perceptual Grouping Theory启发,提出了一种bottom-up的方法。该方法的核心就是采用spatio-temporal embeddings,通过给每一帧每个pixel一个高维度的embedding,将同一个instance的pixel投影到embedding space中相近的位置,使他们属于同一个cluster。
Problem Formulation
假设视频片段共 T T T 帧,分辨率是 H ∗ W H*W H∗W,由于视频是RGB三通道的,因此clip可以表示为 χ ∈ R N ∗ 3 \chi \in R^{N*3} χ∈RN∗3,其中 N = T ∗ H ∗ W N=T*H*W N=T∗H∗W,假设在整个clip中有 K K K个instance。设计的网络需要利用embedding function得到每个instance的时空信息,进而对每个pixel的embedding进行聚类。同时,该方法和传统的有一点不一样,即作者提出的方法还需要估计每一个cluster的中心,以及其方差,从而做到更高效的inference。综上所述,网络可以被看作是一个映射,从原视频 χ \chi χ映射为三部分输出:(1) ε ∈ R N ∗ E \varepsilon \in R^{N*E} ε∈RN∗E,对于每一个pixel得到一个维度为E的embdding;(2) V ∈ R + N ∗ E V \in R^{N*E}_{+} V∈R+N∗E,对于每个pixel,得到一个维度为E的正值方差向量;(3) H ∈ [ 0 , 1 ] N H \in [0,1]^{N} H∈[0,1]N,作为表示instance中心的Heatmap。
对于每一个Instance(假设这里是第j个实例),我们将他建模成一个高斯分布 N ( μ j , ∑ j ) N(\mu_{j},\sum_{j}) N(μj,∑j),所以根据上述的output,在training阶段,由于我们有GT,所以可以通过下式计算出每一个instantce的mean和variance:

对于某一个像素i来说,可以利用其embedding和variance,通过下式来计算属于某个实例j的概率:

所以可以用 C j ^ \hat{C_{j}} Cj^来表示属于第j个instance的像素集合,判断依据是 p i j > 0.5 p_{ij}>0.5 pij>0.5,形式如下:
![]()
因此在training阶段,训练的任务就是找到最优的参数 μ j O P T , ∑ j O P T \mu_{j}^{OPT},\sum_{j}^{OPT} μjOPT,∑jOPT,使得通过GT得到的 C j C_{j} Cj和通过网络计算得到的 C j ^ \hat{C_{j}} Cj^之间的IOU尽可能大,形式如下:

通过上述4个公式,对每一个instance分别进行计算。
Embedding Representation
通过上面的network,可以求得任意维度的embedding特征表示。但是作者考虑到每个pixel的embedding还需要附带上自身的位置信息(因为这些位置信息本身就可以作为一个很好的初始特征),所以采用了一个mixing function ϕ : R E → R E \phi :R^{E}\rightarrow R^{E} ϕ:RE→RE。由于这里是考虑了时空特征,所以属于三维的embedding,对于第i个pixel来说,他的混合函数可表示为: ϕ x y z ( e i ) = e i + [ x i , y i , t i ] \phi_{xyz}(e_{i})=e_{i}+[x_{i},y_{i},t_{i}] ϕxyz(ei)=ei+[xi,yi,ti],这里 e i e_{i} ei的维度E=3,式子表示对应位置做加法。
但是除了上述三个必要的时空维度信息,我们还可以设置额外的free dimension,例如设置E=4,此时混合函数就可以表示为 ϕ x y z f ( e i ) = e i + [ x i , y i , t i , 0 ] \phi_{xyzf}(e_{i})=e_{i}+[x_{i},y_{i},t_{i},0] ϕxyzf(ei)=ei+[xi,yi,ti,0]。这里自由维度的设置可能是把双刃剑,并不是设置的越多越好,具体可以参考实验部分的讨论环节。
Inference
由于Inference阶段没有可用的GT,因此无法通过上面的四个式子计算出每个instance的embedding的均值和方差 μ j , ∑ j \mu_{j},\sum_{j} μj,∑j。所以这里Heatmap就派上用场了,具体流程如下图:

(1)根据Heatmap选出instance的中心点;
(2)找到该中心点所对应的embedding和方差向量;
(3)将该instance的均值和方差用这个中心点所对应的来表示,并通过计算公式(2),来判断某个pixel属于该实例的概率;
(4)由于一些像素已经分配到实例j中,所以为了更长远的考虑,将他们的信息剔除掉
(5)重复1-4的操作,知道Heatmap为空集,或者最大值小于我们设定的threshold。
此外要注意的是,直接将T帧全部塞入内存太大了,所以作者拆分成若干个 T c T_{c} Tc,每一部分之间用Linear Assignment联系起来,具体可以参考代码。
Losses
损失函数由三部分组成:
![]()
(1)embedding loss采用Lov`asz hinge loss来优化GT和预测值之间的IOU,上面已经给了;(2)smmoth loss表示方差部分采用的是smoothness loss,这个损失和CVPR19的一篇实例分割的文章中的很像,可以大体先当作是L1 loss,用于将每个实例的方差回归到他们方差的均值上面;(3)Heatmap loss,采用简单的L2 loss。
Network Architecture

ResNet+FPN,后续对四个不同尺度的特征图分别作3D卷积,然后concat起来。值得注意的是,分辨率大的feature map经过的3D卷积次数最少,因为这里是为了减小内存和计算开销。
实验部分
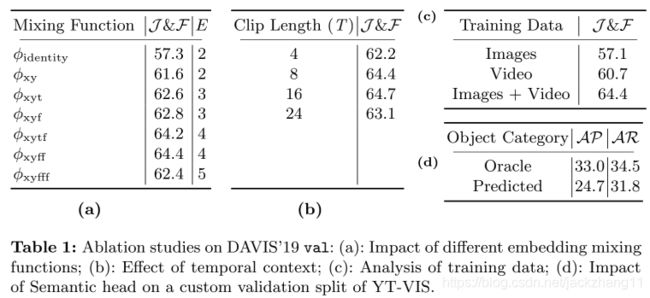
DAVIS19上的消融实验:
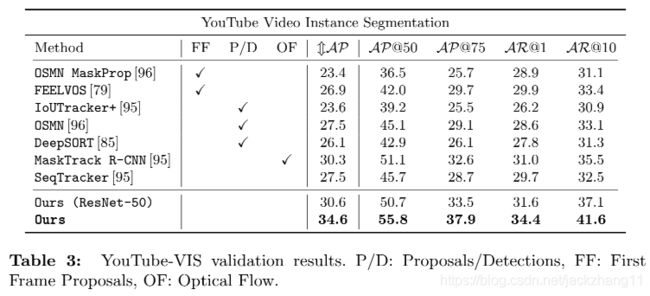
YouTube VIS数据集和其他方法的对比:
MOTS数据集:

总结
作者提出了一个非常简洁的bottom-up的VIS处理流程,实现了end-to-end。相比于其他基于tracking-by-detection的top-down方法来说简化了太多。通过将每一个instance建模成一个涉及到时空特征的高斯分布,来判断其他pixel属于该instance的概率,这里非常巧妙。具体很多细节还要从代码中挖掘。