前言
本文记录了我对打印算法题的总结。先说说什么事打印算法题,就是按照一定的规则打印二维矩阵。例如:旋转正方形矩阵:
1 2 3 4 13 9 5 1
5 6 7 8 ---> 14 10 6 2
9 10 11 12 15 11 7 3
13 14 15 16 16 12 8 4
接下来,将会有几道打印算法题,先看看各个题目的解法,再来总结一下解题方法
例子
1、旋转正方形矩阵
题目
给定一个整型正方形矩阵matrix,请把该矩阵调整成 顺时针旋转90度的样子。
【要求】 额外空间复杂度为O(1)。
例如:
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16
=========
13 9 5 1
14 10 6 2
15 11 7 3
16 12 8 4
【要求】 额外空间复杂度为O(1)
思路:
给定左上角(lx, ly)和右下角(rx, ry)的坐标,确定一个矩阵。对这个矩阵作以下操作:
第一轮,先旋转最外面的矩阵
1,4,16,13作为1组
2,8,15,9作为1组
3,12,14,5作为1组
把以上分组依次交换位置
左上角右下角往中心移动,重复上面的交换步骤,直至lx >= lx
算法实现
public static void rotateMatrix(int[][] matrix){
int lx = 0;
int ly = 0;
int rx = matrix.length - 1;
int ry = matrix[0].length - 1;
while(lx < rx) {
rotateEdage(matrix, lx++, ly++, rx--, ry--);
}
}
public static void rotateEdage(int[][] matrix, int lx, int ly, int rx, int ry) {
// 计算需要交换的次数
int times = rx - lx;
int i = 0;
int tmp = 0;
while(i != times) {
int p4 = matrix[rx - i][ly];
tmp = matrix[lx][ly + i];
matrix[lx][ly + i] = matrix[rx - i][ly];
matrix[rx - i][ly] = matrix[rx][ry - i];
matrix[rx][ry - i] = matrix[lx + i][ry];
matrix[lx + i][ry] = tmp;
i++;
}
}
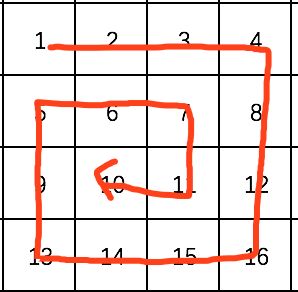
2、转圈打印矩阵
题目
给定一个整型矩阵matrix,请按照转圈的方式打印它。
例如:1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
打印结果为:1,2,3,4,8,12,16,15,14,13,9, 5,6,7,11, 10
【要求】 额外空间复杂度为O(1)。
图解:
思路
设计一个函数,函数功能是给一个左上角和右下角的坐标,打印由这两个点确认的矩形上的点。
然后从原始矩阵的左上角(lx, ly)和右下角(rx, ry)开始打印,打印一圈后,左上角和右下角均往中心移动,即lx++,ly++,rx--, ry--,直至到左 >= 右
算法实现
/// 转圈打印矩阵
public static void printMatrixSpiralOrder(int[][] matrix) {
int lx = 0;
int ly = 0;
int rx = matrix.length - 1;
int ry = matrix[0].length - 1;
// 每打印一趟,左上角和右下角都往中心移动一格
while(lx <= rx && ly <= ry) {
printEdage(matrix, lx++, ly++, rx--, ry--);
}
}
/// 传递左上角(lx, ly),右下角(rx, ry)
/// 打印这个矩阵所有的数
public static void printEdage(int[][] matrix, int lx, int ly, int rx, int ry) {
if(lx == rx) {
// 同行,只移动列
for(int i = ly; i <= ry; i++) {
System.out.print(matrix[lx][i]);
}
}else if(ly == ry) {
// 同列,只移动行
for(int i = lx; i <= rx; i++) {
System.out.print(matrix[i][ly]);
}
}else {
// 不同行,不同列
int x = lx;
int y = ly;
// 打印top
while(y != ry) {
System.out.print(matrix[x][y] + " ");
y++;
}
// 打印left
while(x != rx) {
System.out.print(matrix[x][y] + " ");
x++;
}
// 打印bottom
while(y != ly) {
System.out.print(matrix[x][y] + " ");
y--;
}
// 打印right
while(x != lx) {
System.out.print(matrix[x][y] + " ");
x--;
}
}
}
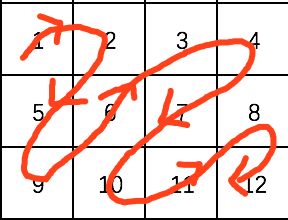
3、"之"字形打印矩阵
题目
给定一个矩阵matrix,按照“之”字形的方式打印这个阵,
例如:1 2 3 4 5 6 7 89 10 11 12 “之”字形打印的结果为:
1,2,5,9,6,3,4,7,10,11, 8,12
【要求】 额外空间复杂度为O(1)。
图解:
思路
同样地,先设计一个函数,作用是给定左下角(lx, ly)和右上角(rx, ry),打印这条直线上的点
首先取(0, 0)作为公共出发点,打印完毕后:
(lx, ly)向下移动,直至到达底部后,ly向右移动
(rx, ry)向右移动,直至到达右边界后,rx向下移动
重复上述过程,直到左下角(lx, ly)和右上角(rx, ry)相遇
算法实现
public static void zhiPrintMatrix(int[][] matrix) {
int lx = 0;
int ly = 0;
int rx = 0;
int ry = 0;
int maxX = matrix.length - 1;
int maxY = matrix[0].length - 1;
boolean isReverse = true;
while(ly != maxY + 1) {
printLine(matrix, lx, ly, rx, ry, isReverse);
isReverse = !isReverse;
// 只有lx到达底部时,ly才移动
ly = lx == maxX ? ly + 1 : ly;
// 先将lx移动到底部
lx = lx == maxX ? lx : lx + 1;
// 只有ry到达右边界时,rx才向下移动
rx = ry == maxY ? rx + 1 : rx;
// 先将ry移动到右边界
ry = ry == maxY ? ry : ry + 1;
}
}
public static void printLine(int[][] matrix, int lx, int ly, int rx, int ry, boolean isReverse) {
if(isReverse) {
// 从左下打印到右上
int x = lx;
int y = ly;
do {
System.out.print(matrix[x][y] + " ");
x--;
y++;
}while(x >= rx && y <= ry);
}else {
// 从右上打印到左下
int x = rx;
int y = ry;
do {
System.out.print(matrix[x][y] + " ");
x++;
y--;
}while(x <= lx && y >= ly);
}
}
总结
通过以上三道题,我们可以总结出以下观点
1、宏观的角度
我们都是从宏观的角度去思考的,而不是想着发掘每一个点(x,y)和(x', y')的关系转换。我们需要在宏观和微观之间平衡,逐步的解剖问题。例如在第一二道题,我们都是通过解决外矩阵后,再解决内矩阵的方式解决问题的。
2、设计一个子模块打印函数
例如给定左上角和右上角打印一个矩阵等打印函数,记住一些常用的打印函数,可以让我们更快地解决问题