数据降维算法总结（LDA&PCA）

LDA

概述

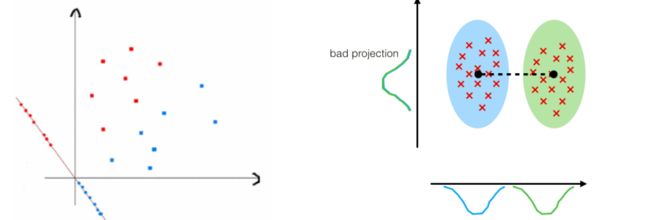
LDA（Linear Discriminant Analysis），线性判别分析。LDA是一种监督学习的降维技术。主要用于数据预处理中的降维、分类任务。LDA的目标是最大化类间区分度的坐标轴成分，将特征空间投影到一个维度更小的k维子空间中，同时保持区分类别的信息。简而言之，LDA投影后的数据类内方差最小，类间方差最大。

数学基础知识

瑞利商
定义：$$R(A,x)=\frac{x^{H}Ax}{x^{H}x}$$
其中，x是非零向量，A是n*n的Hermitan矩阵（自共轭矩阵，矩阵中每一个第i行第j列的元素都与第j行第i列的元素的共轭相等）
性质：瑞利商最大值等于矩阵A最大的特征值，最小值等于矩阵A的最小特征值
$${\lambda }_{min}⩽\frac{x^{H}Ax}{x^{H}x}⩽{\lambda }_{max}$$

广义瑞利商
定义：$$R(A,x)=\frac{x^{H}Ax}{x^{H}Bx}$$
其中，x是非零向量，而A，B为n*n的Hermitan矩阵。B为正定矩阵
最大值为矩阵$B^{-\frac{1}{2}}A{B}^{\frac{-1}{2}}$的最大特征值，或者说矩阵$B^{-1}A$的最大特征值，最小值是其最小特征值

二类LDA原理

假设数据集$D=(x_1,y_1),(x_2,y_2),......,(x_m,y_m)$,其中任意$x_i$为n维向量
第j类样本的均值向量：${\mu }_j=\frac{1}{n_j}\sum x(j=0,1)$
第j类样本的协方差矩阵：${\Sigma }_j=\sum (x-{\mu }_j)(x-{\mu }_j{)}^T(j=0,1)$
假设投影直线是向量$\omega$,则对任意一个样本本xi,它在直线$\omega$的投影为${\omega }^T{x}_i$,对于我们的两个类别的中心点${\mu }_0,{\mu }_1$,在在直线$\omega$的投影为${\omega }^T{\mu }_0$,${\omega }^T{\mu }_1$。由于LDA需要让不同类别的数据的类别中心之间的距离尽可能的大，也就是我们要最大化$||{\omega }^T{\mu }_0-{\omega }^T{\mu }_1|{|}_2^2$,同时我们希望同一种类别数据的投影点尽可能的接近，也就是要同类样本投影点的协方差${\omega }^T{\Sigma }_0\omega$和${\omega }^T{\Sigma }_1\omega$尽可能的小，即最小化${\omega }^T{\Sigma }_0\omega +{\omega }^T{\Sigma }_1\omega$。综上所述，我们的优化目标为：
$$argmaxJ(\omega )=\frac{||{\omega }^T{\mu }_0-{\omega }^T{\mu }_1|{|}_2^2}{{\omega }^T{\Sigma }_0\omega +{\omega }^T{\Sigma }_1\omega }=\frac{{\omega }^T({\mu }_0-{\mu }_1)({\mu }_0-{\mu }_1{)}^T\omega }{{\omega }^T({\Sigma }_0+{\Sigma }_1)\omega }$$
类内散度矩阵$S_{\omega }$为：
$$S_{\omega }={\Sigma }_0+{\Sigma }_1=\sum (x-{\mu }_0)(x-{\mu }_0{)}^T+\sum (x-{\mu }_1)(x-{\mu }_1{)}^T$$
类间散度矩阵$S_b$为：
$$S_b=({\mu }_0-{\mu }_1)({\mu }_0-{\mu }_1{)}^T$$
优化目标重新定义：
$$argmaxJ(\omega )=\frac{{\omega }^T{S}_b\omega }{{\omega }^T{S}_{\omega }\omega }$$
这就是广义瑞利商，最大值就是$S_{\omega }^{-1}{S}_b$的最大特征值

多类LDA原理

优化目标：
$$argmaxJ(\omega )=\frac{\prod {\omega }^T{S}_b\omega }{\prod {\omega }^T{S}_{\omega }\omega }=\prod \frac{{\omega }^T{S}_b\omega }{{\omega }^T{S}_{\omega }\omega }$$
特征向量最多有k-1个

LDA算法流程

1. 计算类内散度矩阵$S_{\omega }$
2. 计算类间散度矩阵$S_b$
3. 计算矩阵$S_{\omega }^{-1}{S}_b$
4. 计算$S_{\omega }^{-1}{S}_b$的最大的d个特征值和对应的d个特征向量$({\omega }_1,{\omega }_2,......,{\omega }_d)$得到投影矩阵W
5. 对样本集中的每一个样本特征$x_i$,转为新的样本$z_i={\omega }^T{x}_i$
6. 得到输出样本集$D^{\prime }=(z_1,y_1),(z_2,y_2),......(z_m,y_m)$

优点

• 在降维过程中可以使用类别的先验知识经验，而像PCA这样的无监督学习则无法使用类别先验知识。
• LDA在样本分类信息依赖均值而不是方差的时候，比PCA之类的算法较优。

缺点

• LDA不适合对非高斯分布样本进行降维，PCA也有这个问题。
• LDA降维最多降到类别数k-1的维数，如果我们降维的维度大于k-1，则不能使用LDA。当然目前有一些LDA的进化版算法可以绕过这个问题。
• LDA在样本分类信息依赖方差而不是均值的时候，降维效果不好。
• LDA可能过度拟合数据。

PCA

概述

PCA（principal component analysis），主成分分析。PCA的主要思想是将n维特征映射到k维上，这k维是全新的正交特征也被称为主成分，是在原有n维特征的基础上重新构造出来的k维特征。
PCA的工作就是从原始的空间中顺序的找一组相互正交的坐标轴，新的坐标轴的选择与数据本身是密切相关的。其中，第一个新坐标轴选择是原始数据中方差最大的方向，第二个新坐标轴选取是与第一个坐标轴正交的平面中使得方差最大，第三个轴是与第1、2个轴正交的平面中方差最大的。以此类推，可以得到n个这样的坐标轴。通过这种方式获得的新的坐标轴，我们发现，大部分方差都包含在前面k个坐标轴中，后面的坐标轴所含的方差几乎为0。于是，我们可以忽略余下的坐标轴，只保留前面k个含有绝大部分方差的坐标轴。事实上，这相当于只保留包含绝大部分方差的维度特征，而忽略包含方差几乎为0的特征维度，实现对数据特征的降维处理。
计算数据矩阵的协方差矩阵，得到协方差矩阵的特征值特征向量，选择特征值最大（方差最大）的k个特征所对应的特征向量组成的矩阵。
由于得到协方差矩阵的特征值特征向量有两种方法：特征值分解协方差矩阵、奇异值分解协方差矩阵

协方差和散度矩阵

协方差
$$Cov(X,Y)=E[(X-E(x))(Y-E(Y))]=\frac{1}{n-1}\sum _{i=1}^n(x_i-\bar{x})(y_i-\bar{y})$$
协方差矩阵

散度矩阵
$$S=\sum _{k=1}^n(x_k-\bar{x})(x_k-\bar{y}{)}^T$$
对于数据X的散度矩阵$X{X}^T$。

特征值分解矩阵原理

1. 计算特征值和特征向量
2. 计算特征值分解矩阵
   

SVD分解矩阵原理

奇异值分解是一个能适用于任意矩阵的一种分解方法，对于任意矩阵A总是存在一个奇异值分解：
$$A=U\Sigma V^T$$
假设A是一个mn的矩阵，那么U是一个mm的方针，U里面的正交向量被称为左奇异向量。$\Sigma$是一个mn的矩阵，$\Sigma$除了对角线其他元素都是0，对角线上的元素称为奇异值。$V^T$是V的转置矩阵，是一个nn的矩阵，它里面的正交向量被称为右奇异值向量。而且一般来讲，我们会将$\Sigma$上的值按从大到小的顺序排列。
SVD分解矩阵A的步骤：

1. 求$A{A}^T$的特征值和特征向量，用单位化的特征向量构成U
2. 求$A^{T}A$的特征值和特征向量，用单位化的特征向量构成V
3. 将$A{A}^T$或者$A^{T}A$的特征值求平方根，然后构成$\Sigma$

PCA的两种实现方法

输入数据集$X=x_1,x_2,......,x_n$，需要降到k维

1. 去平均化（去中心化），即每一位特征减去各自的平均值
2. 计算协方差矩阵
3. 用特征值分解方法求协方差矩阵的特征值和特征向量
4. 用特征值从大到小排序，选择其中最大的k个，然后将其对应的k个特征向量分别作为行向量组成特征向量矩阵P
5. 将数据转换到k个特征向量构建的新空间中，即Y=PX

准则

• 最近重构性：样本集中所有点，重构后的点距离原来的点的误差之和最小
• 最大可分性：样本在低维空间的投影尽可能分开

优点

• 使得数据集更易使用
• 降低算法的计算开销
• 去除噪声
• 使结果容易理解
• 完全无参数限制

缺点

• 如果用户对观测对象有一定的先验知识，掌握了数据的一些特征，却无法通过参数化等方法对处理过程进行干预，可能会得不到预期效果，效率也不高
• 特征值分解有一定的的局限性，比如变换的矩阵必须是方阵
• 在非高斯分布情况下，PCA方法得到的主元可能并不是最优的

算法应用

• 高维数据集的探索和可视化
• 数据压缩
• 数据预处理
• 图像、语音、通信的分析处理
• 降维，取出数据冗余与噪声

LDA vs PCA

• 两者均可以对数据进行降维。
• 两者在降维时均使用了矩阵特征分解的思想。
• 两者都假设数据符合高斯分布。
• LDA是有监督的降维方法，而PCA是无监督的降维方法
• LDA降维最多降到类别数k-1的维数，而PCA没有这个限制。
• LDA除了可以用于降维，还可以用于分类。
• LDA选择分类性能最好的投影方向，而PCA选择样本点投影具有最大方差的方向。

参考

https://www.cnblogs.com/pinard/p/6244265.html
https://blog.csdn.net/program_developer/article/details/80632779

关于作者

知乎