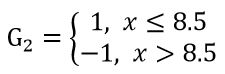知识篇——AdaBoost算法小例

写在前面

新开个分类吧，我发现算法不及时写成简单易懂的总结文档，很快就忘光了。文档的作用，是给未来那个傻逼自己看的。

这两天的任务就是整理之前的算法，先从这个AdaBoost算法开始。凯欣有非常好的总结，戳这里。

另外，这个例子来源是这个：Adaboost算法的原理与推导

我这里给另外一个更简单易懂的例子。后面跟一段小代码，并不是百分之百的AdaBoost实现，分类器是手写的，只为了展示这个例子。

一张算法图

本体

迭代前：

已知样本D：

D

初始化权值e0，e1，…，e9 = 1 / N = 1 / 10 = 0.1

我们给这个添加了权值的样本起个名字，叫做D1：

D1

开始迭代：

（1）选择第一个弱分类器，我们开始第一次迭代：

第一个弱分类器

（为什么选择这样一个迭代器我们最后再说，现在的主要是看AdaBoost算法是如何把多个弱分类器组合成一个强分类器。）

（2）样本经过第一个分类器计算后，结果如下：

（3）可以看到X=6、7、8的三个数据分错了，它们每个权值都是0.1，所以一共是：

（4）于是使用公式计算分类器G1的权重：

（5）现在开始分别更新e0，e1，e2，…，e9，我们先不归一化，先算出每一个未归一化之前的数据权值，使用这个公式：

（6）现在对e0，e1，e2，…，e9进行归一化：

更新为D2结果如下：

（7）这个时候，我们得到了G1的权重，得到了更新了权值的D2。第一次迭代结束。
（8）第二次迭代开始。第一次迭代时使用的是D1，现在我们用D2，过程一样。
（9）先选择一个分类器G2：

G2

计算后得到：

（10）X=3、4、5的三个数据分错了，e = 0.0714 + 0.0714 + 0.0714 = 0.2142
（11）计算G2的权重：

（12）现在开始分别更新e0，e1，e2，…，e9，还是不归一化：

（13）归一化：

（14）更新为D3结果如下：

（15）这时我们得到了G2的权重，得到了D3。第二次迭代结束。

（16）第三次迭代，选择分类器G3，过程略，得到G3的权重 ：

（17）本例只有三个弱分类器它们分别得到了自己的权重，故最后组合而成的分类器如下：

（18）我把x=1、2、3 … 9带入G(x)得：

Sign()应该就是取符号的意思，所以结果为：

可见，G1、G2、G3三个弱分类器被组合成了一个强分类器G，这就是AdaBoost算法。而分类器如何选择，是一个根据情况而定的事情，G1、G2、G3的阈值你可以从0一直试到9，然后把准确率最高的三个阈值分别赋给G1、G2、G3，你也可以选择四个分类器，这是由你自己决定的。

下面是一个简单的代码实现：

# -*- coding: utf-8 -*-
import math

def Step(TestSet, Labels, E_in, g):
    E = E_in
    e_count = 0
    z = 0.0  # 归一化时使用的Z
    R = []  # R 用来存储划判断对错，正确的存1，错误的存-1
    W = []  # W 用来存储 w
    # 第二步，计算在当前划分中的错误个数
    for i in range(10):
        if Labels[i] != g(TestSet[i]):
            R.append(-1)
            e_count += E[i]
        else:
            R.append(1)
    alpha = 0.5 * math.log((1 - e_count) / e_count)
    # 第三步，计算错分错误率综合，由此计算此弱分类器下的权重alpha
    for i in range(10):
        w = E[i] * math.exp(-1 * alpha * R[i])
        W.append(w)
        z += w
    # print z
    for i in range(10):
        E[i] = W[i] / z
    # print E
    return alpha, E

def AdaBoost(x, TestSet, Labels):
    # x 代表要进行判断的数字，测试集，标签集，layer代表若分类器的个数
    E1 = []  # E 用来存储错误值
    for i in range(10):
        E1.append(0.1)
    alpha_1, E2 = Step(TestSet, Labels, E1, G1)
    alpha_2, E3 = Step(TestSet, Labels, E2, G2)
    alpha_3, E4 = Step(TestSet, Labels, E3, G3)
    # print 'alpha_3: ', alpha_3
    return (alpha_1 * G1(x)) + (alpha_2 * G2(x)) + (alpha_3 * G3(x))

def G1(x):
    if x < 2.5:
        return 1
    else:
        return -1


def G2(x):
    if x < 8.5:
        return 1
    else:
        return -1


def G3(x):
    if x < 5.5:
        return -1
    else:
        return 1

def AdaBoostCalculate(x, layer=3, step=1):
    # x 代表要进行判断的数字，layer代表若分类器的个数
    TestSet = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
    Labels = [1, 1, 1, -1, -1, -1, 1, 1, 1, -1]
    AdaBoost(1, TestSet, Labels)
    for i in range(10):
        print AdaBoost(i, TestSet, Labels)
    return 0

print AdaBoostCalculate(3)

输出的结果就是重新把X=0、1、2 ... 9用最终分类器计算的结果，如下：

0.321251723871
0.321251723871
0.321251723871
-0.526046136517
-0.526046136517
-0.526046136517
0.97803126026
0.97803126026
0.97803126026
-0.321251723871

这个结果，就是（18）中的计算值。

---

我们的822，我们的青春
欢迎所有热爱知识热爱生活的朋友和822实验室一起成长，吃喝玩乐，享受知识。