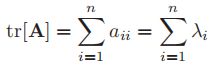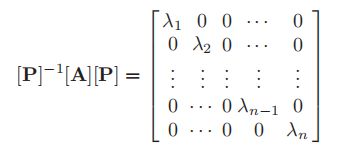特征值问题编程基础：特征值特征向量的求解和性质

第二十四篇 特征值问题编程基础：特征值特征向量的求解和性质

特征值方程

在分析结构稳定性或振动系统的固有频率时，经常会出现这种情况。我们必须找到一个向量{x}，当它与[a]相乘时，得到它自身的标量倍。这个λ倍数称为[A]的“特征值”，我们将看到n阶矩阵有n个这样的λ。从物理上讲，它们可能代表振荡的频率。还有与每个特征值λ相关的n个向量{x}。这些被称为“特征向量”。从物理上讲，它们可能代表振荡的模态振型。下面是一个具体的例子：

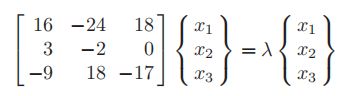
重新排列后可以写成下面的形式

这组线性联立方程只有在系数的行列式为零时才可能有非0解

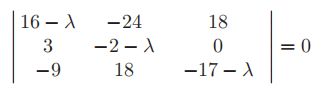
行列式展开得

这叫做“特征多项式”。显然，解特征值方程的一种方法是将其简化为一个n次特征多项式，并使用前一章的方法来求其根。有时这样做，也许作为整个解过程的一部分，但它本身通常不是求解特征值方程的最佳方法。
上面得特征多项式有一个简单得因式分解

所以特征值解为4，1，-8
对于任意矩阵[A]，特征多项式都可能产生虚根和实根。所以要把问题限制在具有实数特征值的矩阵上，物理约束通常意味着矩阵是对称的和“正定的”，在这种情况下，所有的特征值都是实数和正数。找到一个特征值后，其相关的特征向量可以通过求解一组线性联立方程来找到。例如，将λ = 1代入方程得到

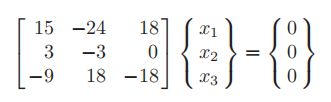
经过高斯消元得第一个阶段

由上面可以看出，行列式得值为0，方程数比未知数数量少，可见方程组是线性相关的。然而，我们可以从上面的方程第二行和第三行看出，x2与x3的比值是2:1，通过代换方程的第一行，x1与x2的比值是1:1。所以当特征值λ = 1时，任意一个特征向量的比值x1: x2: x3 = 2:2:1。类似的操作也可以用来求两个特征值对应的特征向量。

特征向量的正交化和规范化

特征向量有一个独特的方向，但它们的大小是任意的。两边同时乘以一个任意常数α，得到。

在该修正方程中，α{x}和{x}是数组[A]中对应特征值λ的等效特征向量。两种常用的特征向量正交化方法。对于下面的对称矩阵

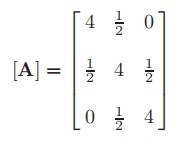
具有特征值

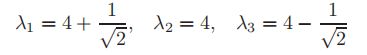
对应的特征向量

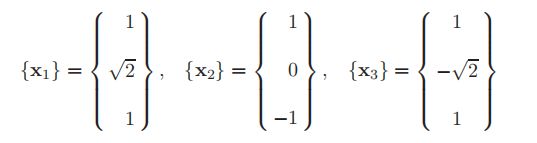
特征向量正交化的一种简便形式包括缩放长度，或者称为“L2范数”或“欧几里德范数”。因此对于一个特征向量的n个分量，我们像下面这个缩放这个向量

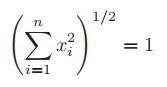
它是累加全部分量的平方和再求跟得到的
因此，对于第一个特征向量，将除以下面这个长度值

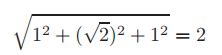
对于其他两个特征向量，得到正交特征向量为

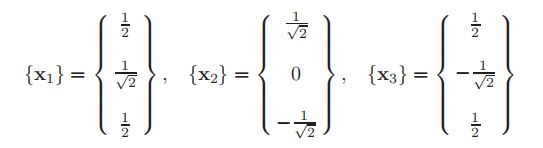
对称矩阵的特征向量互相具有“正交性”。也就是说，来自同一个矩阵的任意两个不同特征向量的点积等于零，而特征向量与自身的点积为其长度的平方。因此，将欧几里德范数设为单位1的一个便利的特点是是特征向量点积要么等于零，要么等于单位1。

特征向量正交化的一种简单的替代形式是除以具有最大(绝对)幅度的分量。得到了一个最大分量等于单位1的正交化特征向量。对于之前给出的特征向量，第一个特征向量除以√2，第二个特征向量不变，因第三个特征向量将被-√2整除得到正交化向量。

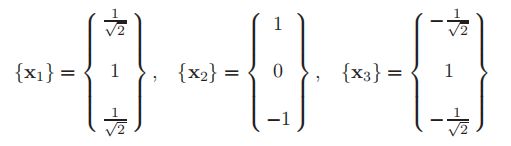
特征值和特征向量的性质

本部分所描述的数值方法利用了很多矩阵变换对特征值和特征向量影响的定理。下面总结了这些关系中使用较多的一些。

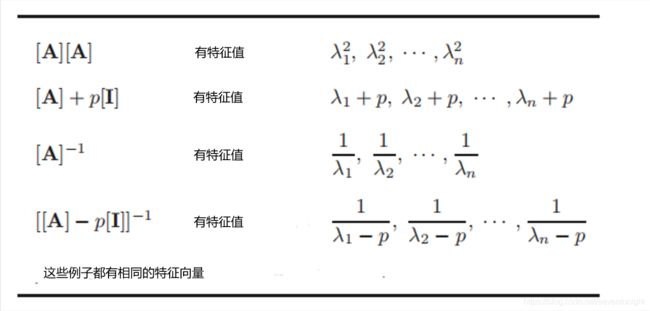
如果一个n × n矩阵[A]具有实数特征值λ1， λ2，···，λn， [I]为单位矩阵，p为标量位移，则

n × n矩阵对角线的和称为“迹”，也等于特征值的和，因此

一个n×n矩阵的特征值的乘积等于这个矩阵的行列式，因此

一个n × n三角形矩阵的对角线是特征值。

给定两个方阵[A]和[B]。

[A][B]和[B][A]将有相同的特征值。
如果{x}是[A][B]的特征向量，则[B]{x}是[B][A]的特征向量。
解释：

然后两边都乘以B得到

给定两个方阵[A]和[P]，其中[P]是非0的。

[A]和[P]−1[A][P]具有相同的特征值。
如果{x}是[A]的特征向量，那么[P]−1{x}是[P]−1[A][P]的特征向量。
解释：

通过两边都乘以[P]−1，得到

嵌入矩阵形式[P][P]-1=[I]，得到

如果[A]是一个n×n矩阵，其特征值和特征向量为λ1{x1}， λ2{x2}，···，λn{xn}。[P]是一个矩阵，其列是[a]的使其欧几里德范数等于单位的特征向量缩放，那么