第12届蓝桥杯参赛心路历程及部分题解

本人大一，第一次参加蓝桥杯，蓝桥杯也是我参加的第一场大赛，真的很紧张，估摸着感觉运气的成分特别大，做出来了七道题，四道填空题三道编程题，后来对了对答案，填空题对了三道，编程题应该是没办法过全部数据，结果居然拿到了省一，有点出乎意料，听完Y总的讲解更是收益匪浅，那就大致写写我在赛场上的心路历程以及我对每道题的一些分析思路。

试题A. 空间

这道水题没啥好说的，但凡了解一点计算机的都不会错，不需要借助编程，注意单位转换 1MB = 1024 KB = 1024 * 1024 B，32 bit = 4 B 用计算器就可以解决
答案：67108864

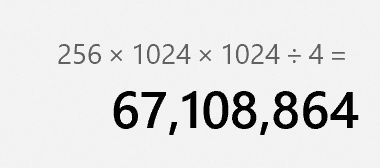
试题B.卡片

这题表面上问我们2021个0到9的数字能组成到第多少个数，但其实就是问到多少个数里面包含2021个1， 因为1永远是最先被用到的，也肯定是最先被用完的。代码如下
答案：3181

#include
using namespace std;
int cnt ;
int main(void)
{
     
    for (int i = 1 ;; i++) {
     
        int temp = i ;
        while (temp) {
     
            if (temp % 10 == 1) cnt++ ;
            temp /= 10 ;
        }
        if (cnt == 2021) {
     
            cout << i ;
            break ;
        }
        if (cnt > 2021) {
     
            cout << i - 1 ;
            break ;
        }
    }
    return 0 ;
}

试题C. 直线

这题很可惜错了，思路大体上是对的，利用数学公式把直线的斜率和截距表示出来，我想着用集合去重，后来输出集合大小应该就没问题了，但是后来才想起来用浮点数去存k和b会有误差导致无法完全相等无法去重，所以这条路子不好走通，于是换条路子，利用结构体数组将每组k和b进行排序，然后如果相差足够小就当做相等， 这里要注意下当k不存在的情况需要特判一下。
答案：40257

#include
#include
#include
using namespace std;
const int N = 200000 ;
int res, n ;
struct node
{
     
    double k ;
    double b ;
}arr[N];
bool cmp(node x, node y)
{
     
    if (x.k == y.k) return x.b < y.b ;
    return x.k < y.k ;
}
int main(void)
{
     
    for (int x1 = 0 ; x1 < 20 ; x1++) {
     
        for (int y1 = 0 ; y1 < 21 ; y1++) {
     
            for (int x2 = 0 ; x2 < 20 ; x2++) {
     
                for (int y2 = 0 ; y2 < 21 ; y2++) {
     
                    if(x1 != x2) {
     
                        double k = (double)(y1 - y2) / (x1 - x2) ;
                        double b = (double)(y1 - k * x1 ) ;
                        arr[n++] = {
     k, b} ;
                    }
                }
            }
        }
    }
    sort(arr, arr + n, cmp) ;
    for (int i = 1 ; i < n ; i++) {
     
        if (fabs(arr[i].k - arr[i - 1].k) > 1e-8 || fabs(arr[i].b - arr[i - 1].b) > 1e-8)
         res++ ;
    }
    cout << res + 20 ;
    return 0 ;
}

试题D.货物摆放

这题我第一眼看以为是暴力剪枝，毕竟蓝桥杯又名暴力杯，某位dalao曾和我说他有一次打蓝桥杯有一个代码跑了两个小时，让我铭记于心，结果这一次我一直跑到比赛结束都没有跑出来…
↓错误TLE代码

#include
using namespace std;
long long N = 2021041820210418 ;
long long num ;
int main(void)
{
     
	for (long long i = 1 ; i <= N ; i++) {
     
		if (N % i == 0) {
     
            int temp = N / i ;
            for (long long j = 1 ; j <= temp ; j++) {
     
                if (temp % j == 0) num++ ;
            }
		}
	}
	cout << num ;
	return 0 ;
}

现在想想但凡算一下时间复杂度也都知道根本出不来，所以必须换一个思路，先把2021041820210418的所有因子求出来，在进行暴力循环，这样可以大大降低时间复杂度,
答案：2430
↓正确AC代码

#include
#include
#include
using namespace std;
long long cnt ;
vector<long long> vec ;
void get_factor(long long n)
{
     
    for (int i = 1 ; i <= sqrt(n) ; i++) {
     
        if (n % i == 0) {
     
            vec.push_back(i) ;
            vec.push_back(n / i) ;
        }
    }
}
int main(void)
{
     
    get_factor(2021041820210418);
    for (long long i = 0 ; i < vec.size() ; i++) {
     
        for (long long j = 0 ; j < vec.size() ; j++) {
     
            for (long long z = 0 ; z < vec.size() ; z++) {
     
                if (vec[i] * vec[j] * vec[z] == 2021041820210418) cnt++ ;
            }
        }
    }
    cout << cnt ;
    return 0 ;
}

这道在我能力范围内的题没做出来真的很可惜！！！！

试题E.路径

这道题乍一看是一道最短路，其实它就是一道最短路， 而且是填空题，不需要考虑时间复杂度，什么最短路算法都能往上写，但是在比赛场上的我没有用最短路也做出来了(其实就是太菜了根本不会最短路算法，别骂了孩子知错了)，我用的是自以为正确的数学分析外加一点点的蒙居然做(meng)出来了，简直幸运值拉满。

↓我的赛场分析过程(看看就好别当真)：
这道题大意是说在绝对值小于21的两个数字之间有无向边，无向边长为两数字的最小公倍数，作为我唯一会的数论：

int gcd(int x, int y) // 求最大公因数
{
     
    return y? gcd(y, x % y) : x ;
}
int lcm(int x, int y) //求最小公倍数
{
     
    return x * y / gcd(x, y) ;
}

那么想要每一步最小公倍数最小，那就让最大公因数最大即可，每一步之间的最大公因数其实就是在1到21之间，那么如果每一步都走到21的倍数，它们的最大公因数应该最大，最小公倍数就能最小，所以就是从1开始：1，21，42，63…一直到2016，最后再加上2016和2021的最小公倍数，总距离应该就是最小的了。代码如下：

#include
using namespace std;
int gcd(int x, int y)
{
     
    return y? gcd(y, x % y) : x ;
}
int lcm(int x, int y)
{
     
    return x * y / gcd(x, y) ;
}
int main(void)
{
     
    long long num = 1 * 21 / gcd(1, 21) ;
    for (int i = 42; i <= 2016 ; i += 21) {
     
        num += (i - 21) * i / gcd(i, i - 21) ;
    }
    num += 2016 * 2021 / gcd(2016, 2021) ;
    cout << num ;
    return 0 ;
}

最后结果是10266837，没有很严谨的数学证明，只能说是运气好，大脑的自以为是对的好像真的是对的，要是因为不会最短路算法丢掉这一题那就太亏了。最短路的版本题解也将放在后续。

填空题总结

这五道选择题就我而言是在能力范围之内的，并不难，错了两道确实可惜，只能说自己在比赛场上对题目的分析还不够全面，不能每次都找到题目的最优解，当时为了跑出那个试题D，我还开了两个编译器，我对时间复杂度的计算也不够熟练，或者说还没有养成取计算时间复杂度的这个习惯，感觉自己的提升空间还很巨大，赶紧冲刺复习下一些基础算法争取在国赛上面别丢脸qwq