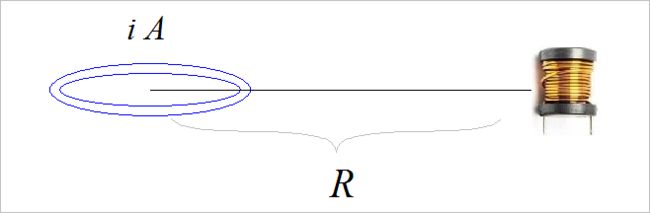
分析无线充电线圈在自绕工字型电感中的感应电动势
01 线圈中的电动势
1.分析的背景
在这两天就设计用于 全国大学生智能汽车竞赛 中的 节能信标组 使用无线充电150kHz的信号进行导航的无线电检测放大电路的进行研究。博文 选频放大电路对于150kHz导航信号进行放大检波 论证了信标无线充电线圈周围交变磁场强的公式:
b ( r , m ) = 2 μ 0 4 π cos θ R 3 ⋅ i ⋅ A b\left( {r,m} \right) = { {2\mu _0 } \over {4\pi }}{ {\cos \theta } \over {R^3 }} \cdot i \cdot A b(r,m)=4π2μ0R3cosθ⋅i⋅A
-
其中:
-
μ 0 \mu _0 μ0 : 真空磁导率(Permeability of Vacuum)-
4 π × 1 0 − 7 N / A 2 4\pi \times 10^{ - 7} \,N/A^2 4π×10−7N/A2
R R R:距离
i i i:电流
A A A:面积
其中, i ⋅ A = m i \cdot A = m i⋅A=m又被定义为线圈对应的磁偶极子的磁矩。
下面来计算在距离它0.65米处的自行绕制的工字型电感感应电动势的大小。验证是否是测量的相同
2.法拉第磁感应定律
如果线圈中的磁场发生改变,则产生的电动势为:
E = − N ⋅ d Φ B d t E = - N \cdot { {d\Phi _B } \over {dt}} E=−N⋅dtdΦB
-
其中参数:
-
Φ B \Phi _B ΦB:是线圈的磁通量,
Φ B = ∫ B ⃗ ⋅ d A ⃗ = ∫ B cos ϕ ⋅ d A \Phi _B = \int_{}^{} {\vec B \cdot d\vec A} = \int_{}^{} {B\cos \phi \cdot dA} ΦB=∫B⋅dA=∫Bcosϕ⋅dA
N:线圈匝数。
电流产生磁场方向可以由 右手定则 确定。Lenz定律要求感应电动势所产生的电流抵消磁场变化。
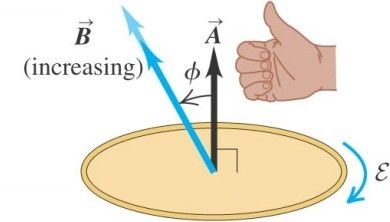
▲ 产生正向感应电动势方向
因此,求取天线附近的磁通量 N ⋅ Φ B N \cdot \Phi _B N⋅ΦB是计算感应电动势的关键。
3.磁感应强度
如果假设在线圈同一平面上, θ = 0 \theta = 0 θ=0;取 i ⋅ A = 0.675 A ⋅ m 2 i \cdot A = 0.675\,\,\,A \cdot m^2 i⋅A=0.675A⋅m2; R = 0.65 m R = 0.65m R=0.65m。那么电感所在区域的磁感应强度为: B = 2 ⋅ 4 π ⋅ 1 0 − 7 4 π ⋅ 1 0.6 5 3 ⋅ 0.675 = 4.916 × 1 0 − 7 B = { {2 \cdot 4\pi \cdot 10^{ - 7} } \over {4\pi }} \cdot {1 \over {0.65^3 }} \cdot 0.675 = 4.916 \times 10^{ - 7} B=4π2⋅4π⋅10−7⋅0.6531⋅0.675=4.916×10−7
▲ 位于线圈同一平面上的感应线圈
根据工字型磁芯的尺寸,直径等于为11.55mm。因此它的横截面积为: A = π ⋅ ( d 2 ) 2 = π 0.0115 5 2 4 = 1.048 × 1 0 − 4 A = \pi \cdot \left( { {d \over 2}} \right)^2 = \pi { {0.01155^2 } \over 4} = 1.048 \times 10^{ - 4} A=π⋅(2d)2=π40.011552=1.048×10−4
绕制匝数 N = 60 N = 60 N=60,那么磁通量为:$ N ⋅ Φ B = N ⋅ A ⋅ B = 60 × 1.048 × 1 0 − 2 × 4.916 × 1 0 − 7 = 3.09 × 1 0 − 9 N \cdot \Phi _B = N \cdot A \cdot B = 60 \times 1.048 \times 10^{ - 2} \times 4.916 \times 10^{ - 7} = 3.09 \times 10^{ - 9} N⋅ΦB=N⋅A⋅B=60×1.048×10−2×4.916×10−7=3.09×10−9
4.感应电动势
根据磁场变化频率 f 0 = 150 k H z f_0 = 150kHz f0=150kHz,那么感应电动势 E 0 = 2 2 ⋅ 2 π ⋅ f 0 ⋅ N ⋅ Φ B = 2 2 ⋅ 2 π ⋅ 150 k ⋅ 3.09 × 1 0 − 9 = 2.06 m V E_0 = { {\sqrt 2 } \over 2} \cdot 2\pi \cdot f_0 \cdot N \cdot \Phi _B = { {\sqrt 2 } \over 2} \cdot 2\pi \cdot 150k \cdot 3.09 \times 10^{ - 9} = 2.06mV E0=22⋅2π⋅f0⋅N⋅ΦB=22⋅2π⋅150k⋅3.09×10−9=2.06mV
02 实测数据对比
1.谐振天线
(1)谐振电压
在 选频放大电路对于150kHz导航信号进行放大检波 ,给工字型电感配制了谐振电容,将其放置在距离无线充电线圈附件0.7mi,测量谐振电压为:5.432mV。
(2)天线Q值
在前面博文中,使用DG8SAQ测量谐振回路在谐振是,等效并联电阻为1.515kΩ。
电感, L 0 = 188.75 μ H L_0 = 188.75\mu H L0=188.75μH,频率 f 0 = 150 k H z f_0 = 150kHz f0=150kHz,对应的电抗 X 0 = 2 π f 0 ⋅ L 0 = 2 π × 150 k × 188.75 μ = 177.89 X_0 = 2\pi f_0 \cdot L_0 = 2\pi \times 150k \times 188.75\mu = 177.89 X0=2πf0⋅L0=2π×150k×188.75μ=177.89
所以线圈的Q值为: Q = R ∣ ∣ X 0 = 1.515 177.89 = 8.516 Q = { {R_{||} } \over {X_0 }} = { {1.515} \over {177.89}} = 8.516 Q=X0R∣∣=177.891.515=8.516
(3)感应电动势
根据谐振电压以及线圈Q值,那么实际感应电压: E e m f = U 0 Q = 5.432 8.516 = 0.638 m V E_{emf} = { {U_0 } \over Q} = { {5.432} \over {8.516}} = 0.638mV Eemf=QU0=8.5165.432=0.638mV
对比前面计算出的2.06mV,只能说明它们在同一数量级,但数据大小还是相差很大的。
2.仔细对比
如果将 E e m f E_{emf} Eemf乘以 π \pi π,那么它等于 π ⋅ E e m f = 0.638 × π = 2.004 m V \pi \cdot E_{emf} = 0.638 \times \pi = 2.004mV π⋅Eemf=0.638×π=2.004mV
这个数字就与上面计算出 2.06没V非常接近了。
※ 分析总结
本文利用法拉第定律计算了距离无线节能组0.6米福建的自绕工字型电感内部的感应电动势,验证了计算公式的正确性,这为后来分析放大过程提供了理论支持。
如果希望将分析的距离R放大到10米左右,那么感应电动势的大小减少1000倍,那么感应电动势就基本上为几个微伏,这个电压靠近器件的热噪声。
■ 相关文献链接:
- 第十六届全国大学智能汽车竞赛竞速比赛规则
- 节能信标无线感应定位测试:200kHz
- 选频放大电路对于150kHz导航信号进行放大检波
- 右手定则