讨论的问题:综合考虑胜率与薪资,OKA球队相比其他的球队是否有竞争性优势。
数据来源:http://seanlahman.com/files/database/lahman-csv_2014-02-14.zip
1、从网络上下载需要的CSV文档,这里采用request,stringIO,zipfile进行数据提取:
def getZIP(zipFileName):
#以字节的方式请求
r = requests.get(zipFileName).content
#创建内存文件
s = StringIO.StringIO(r)
zf = zipfile.ZipFile(s,'r')
return zf
url = 'http://seanlahman.com/files/database/lahman-csv_2014-02-14.zip'
zf = getZIP(url)
数据展示如下:
['SchoolsPlayers.csv', 'SeriesPost.csv', 'Teams.csv', 'TeamsFranchises.csv', 'TeamsHalf.csv', 'AllstarFull.csv', 'Appearances.csv', 'AwardsManagers.csv', 'AwardsPlayers.csv', 'AwardsShareManagers.csv', 'AwardsSharePlayers.csv', 'Batting.csv', 'BattingPost.csv', 'Fielding.csv', 'FieldingOF.csv', 'FieldingPost.csv', 'HallOfFame.csv', 'Managers.csv', 'ManagersHalf.csv', 'Master.csv', 'Pitching.csv', 'PitchingPost.csv', 'readme2013.txt', 'Salaries.csv', 'Schools.csv']
这里把需要的salaries和teams这两个CSV文件读取出来:
salaries = pd.read_csv(zf.open(tablenames[tablenames.index('Salaries.csv')]))
print salaries.head()
teams = pd.read_csv(zf.open(tablenames[tablenames.index('Teams.csv')]))
#这里只需要这几列
teams = teams[['yearID', 'teamID', 'W']]
print teams.head()
yearID teamID lgID playerID salary
0 1985 BAL AL murraed02 1472819
1 1985 BAL AL lynnfr01 1090000
2 1985 BAL AL ripkeca01 800000
3 1985 BAL AL lacyle01 725000
4 1985 BAL AL flanami01 641667
yearID teamID W
0 1871 PH1 21
1 1871 CH1 19
2 1871 BS1 20
3 1871 WS3 15
4 1871 NY2 16
接下来计算各个队每年的总工资,并把两个列表合并起来,W代表胜场:
#一般情况下,聚合数据都需要唯一的分组键组成的索引,但也可以通过向groupby传入as_index=False以禁用该功能
totleSalaries = salaries.groupby(['yearID','teamID'],as_index=False).sum()
print totleSalaries.head()
#how="inner"指当左右两个对象存在不重合的键时,inner 代表交集;outer 代表并集;on指的是用于连接的列索引名称,如果没有指定且其他参数也未指定则以两个DataFrame的列名交集做为连接键
joined = pd.merge(totleSalaries, teams, how="inner", on=['yearID', 'teamID'])
print joined.head()
yearID teamID salary
0 1985 ATL 14807000
1 1985 BAL 11560712
2 1985 BOS 10897560
3 1985 CAL 14427894
4 1985 CHA 9846178
yearID teamID salary W
0 1985 ATL 14807000 66
1 1985 BAL 11560712 83
2 1985 BOS 10897560 81
3 1985 CAL 14427894 90
4 1985 CHA 9846178 85
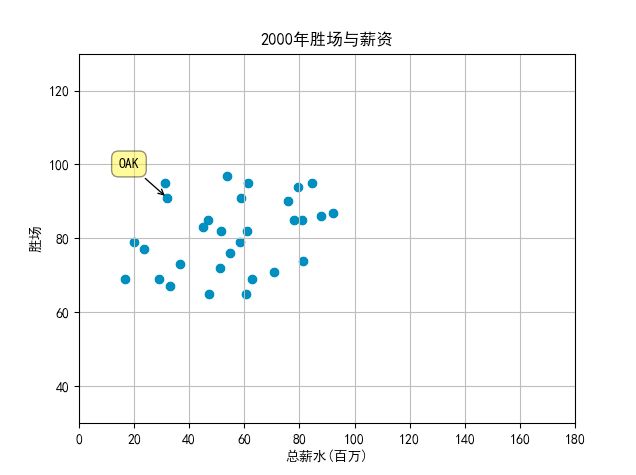
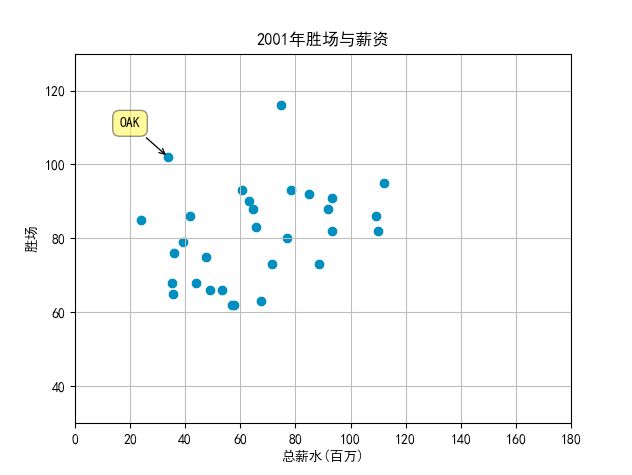
接下来画出各个球队每年总的薪水和获胜次数的关系图,并标记处OKA这只球队:
teamName ='OAK'
years = np.arange(2000,2004)
for year in years:
df = joined[joined['yearID'] == year]
print df
#画出薪资和胜场的散点图
plt.scatter(df['salary'] / 1e6,df['W'])
plt.title(str(year)+'年'+'胜场与薪资')
plt.xlabel('总薪水(百万)')
plt.ylabel('胜场')
plt.xlim(0, 180)
plt.ylim(30, 130)
plt.grid()
#标记出OKA球队
plt.annotate(teamName,
xy=(df['salary'][df['teamID'] == teamName] / 1e6, df['W'][df['teamID'] == teamName]),
xytext=(-20, 20), textcoords='offset points', ha='right', va='bottom',
bbox=dict(boxstyle='round,pad=0.5', fc='yellow', alpha=0.5),
arrowprops=dict(arrowstyle='->', facecolor='black', connectionstyle='arc3,rad=0'))
plt.show()
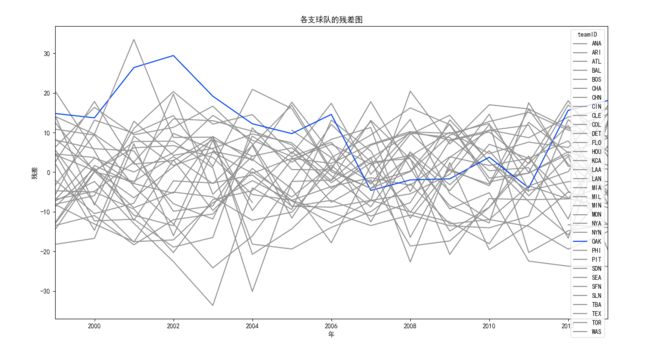
可以看出OKA的在2000年到2004年间付出总薪水较少的情况下获得了比较好的胜利场数,接下来用回归分析证明这一点,并看看更长时间内的数据怎么样,算出各支球队的残差,就能知道是否如上述推论:
teamName = 'OAK'
years = np.arange(1999, 2014)
def Residual(year):
residData = pd.DataFrame()
df = joined[joined['yearID'] == year]
#原始数据横坐标
x_list = df['salary'].values / 1e6
#纵坐标
y_list = df['W'].values
#最小二乘估计
A = np.array([x_list, np.ones(len(x_list))])#构造系数矩阵
y = y_list
w = np.linalg.lstsq(A.T,y)[0] #求出斜率以及纵截距,w[0]斜率w[1]纵截距
yhat = (w[0]*x_list+w[1]) # 回归线
residData['teamID'] = df['teamID']
residData[year] = y - yhat
residData.index = residData['teamID']
residData = residData.drop(residData.columns[0], axis=1)
#print residData
return residData
#将dataframe放入数组
Residuals = [Residual(year) for year in years]
#按照队名合并
Residual_df = reduce(lambda left,right:pd.merge(left,right,how='outer',left_index=True, right_index=True),Residuals)
print Residual_df
Residual_df = Residual_df.T
Residual_df.plot(title = '各支球队的残差图', figsize = (15, 8),
color=map(lambda x: 'blue' if x==teamName else 'gray',Residual_df.columns))
plt.xlabel('年')
plt.ylabel('残差')
plt.show()
这里主要在于如何将多个将dataframe拆分成多个小的dataframe并重新按照不重合的主键名合并。
如图可以看出,在2000年到2003年间,OKA球队偏移回归线较远,且残差为正,说明其能在付出较少薪水的情况下获得较好的成绩,特别是在2002与2003年,偏移最远,此时球队的性价比在联盟中应该是最高的。但在2004年后,残差往负的方向走,并持续多年,说明此时球队成绩不太好,但在2010年后有复苏的趋势。