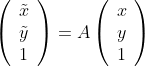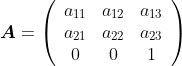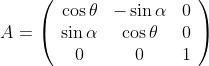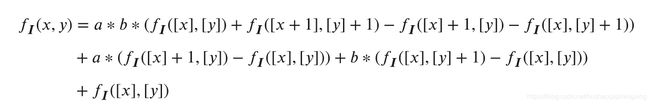敲键盘的钢琴师

OpenCV——几何变换

目录

3.1仿射变换

3.1.1 平移

3.1.2 放大和缩小

3.1.3 旋转

3.1.4 计算仿射矩阵

3.1.5 插值算法

3.1.6 旋转函数Rotate

3.2投影变换

3.3极坐标变换

1. 将笛卡儿坐标转换为极坐标

2. 将极坐标转换为笛卡儿坐标

3. 利用极坐标变换对图像进行变换

3.1仿射变换

基本的仿射变换类型：平移、缩放、旋转。变换过程就是构造仿射变换矩阵A。

$\left(\begin{array}{l}{\tilde{x}} \\ {\tilde{y}} \\ {1}\end{array}\right)=A\left(\begin{array}{l}{x} \\ {y} \\ {1}\end{array}\right)$ ， $\boldsymbol{A}=\left(\begin{array}{ccc}{a_{11}} & {a_{12}} & {a_{13}} \\ {a_{21}} & {a_{22}} & {a_{23}} \\ {0} & {0} & {1}\end{array}\right)$ ，引入第三个数值为1的坐标，实现齐次坐标。

3.1.1 平移

$(\tilde{x}, \tilde{y})=\left(x+t_{x}, y+t_{y}\right)$ ，假设任意空间坐标 $(\mathrm{x}, \mathrm{y})$ ，沿x轴平移 $t_{x}$ ,再沿y轴平移 $t_{\mathrm{y}}$

$\left(\begin{array}{c}{\tilde{x}} \\ {\tilde{y}} \\ {1}\end{array}\right)=\left(\begin{array}{ccc}{1} & {0} & {t_{x}} \\ {0} & {1} & {t_{y}} \\ {0} & {0} & {1}\end{array}\right)\left(\begin{array}{l}{x} \\ {y} \\ {1}\end{array}\right)$

3.1.2 放大和缩小

$(\tilde{x}, \tilde{y})=\left(x_{0}+s_{x}\left(x-x_{0}\right), y_{0}+s_{y}\left(y-y_{0}\right)\right)$ ,显然，缩放后的坐标位置离中心点的水平距离变为原来的sx倍，离中心点的垂直距离变为原来的sy 倍。可以将该变换过程理解为先将原点平移到中心点，再以原点为中心进行缩放，然后移回坐标原点，用矩阵形式可以表示为：

$\left(\begin{array}{c}{\tilde{x}} \\ {\tilde{y}} \\ {\tilde{y}}\end{array}\right)=\left(\begin{array}{ccc}{1} & {0} & {x_{0}} \\ {0} & {1} & {y_{0}} \\ {0} & {0} & {1}\end{array}\right)\left(\begin{array}{ccc}{s_{x}} & {0} & {0} \\ {0} & {s_{y}} & {0} \\ {0} & {0} & {1}\end{array}\right)\left(\begin{array}{ccc}{1} & {0} & {-x_{0}} \\ {0} & {1} & {-y_{0}} \\ {0} & {0} & {1}\end{array}\right)\left(\begin{array}{l}{x} \\ {y} \\ {1}\end{array}\right)$ ，（从右往左计算）

这里显示了齐次坐标的优势，以任意一点为中心的缩放仿射变换矩阵是平移矩阵和以（0，0）为中心的缩放仿射变换矩阵组合相乘而得到的。

3.1.3 旋转

首先计算顺时针旋转后的坐标 $(\tilde{x}, \tilde{y})$ ， $\cos \theta=\frac{x}{p}, \sin \theta=\frac{y}{p}$ ，其中p代表（x，y）到中心点（0，0）的距离，则

$\cos (\theta+\alpha)=\cos \theta \cos \alpha-\sin \theta \sin \alpha=\frac{x}{p} \cos \alpha-\frac{y}{p} \sin \alpha=\frac{\tilde{x}}{p}$

$\sin (\theta+\alpha)=\sin \theta \cos \alpha+\cos \theta \sin \alpha=\frac{y}{p} \cos \alpha+\frac{x}{p} \sin \alpha=\frac{\tilde{y}}{p}$

化简以上两个公式，可得 $\tilde{X}=\mathrm{x} \cos \alpha-y \sin \alpha$ , $\tilde{y}=x \sin \alpha+y \cos \alpha$ 用矩阵形式表示为：

$\left(\begin{array}{c}{\tilde{x}} \\ {\tilde{y}} \\ {1}\end{array}\right)=\left(\begin{array}{ccc}{\cos a} & {-\sin \alpha} & {0} \\ {\sin \alpha} & {\cos \alpha} & {0} \\ {0} & {0} & {1}\end{array}\right)\left(\begin{array}{l}{x} \\ {y} \\ {1}\end{array}\right)$ ，令 $A=\left(\begin{array}{ccc}{\cos \theta} & {-\sin \alpha} & {0} \\ {\sin \alpha} & {\cos \theta} & {0} \\ {0} & {0} & {1}\end{array}\right)$

3.1.4 计算仿射矩阵

对于空间变换的仿射矩阵有两种计算方式：解方程组法和基本仿射变换矩阵相乘法；

1、方程法：仿射变换矩阵有六个未知数，所以只需要三组对应位置的坐标，构造出由六个方程组成的方程组即可解六个未知数。

OpenCV提供的函数： cv2.getAffineTransform(src, dst)

就是通过方程法计算参数src到dst的对应仿射变换矩阵的。对于该函数的Py thonAPI，输入参数src和dst分别代表原坐标和变换后的坐标，且均为3行2列的二维ndarray，每一行代表一个坐标，且数据类型必须为浮点型，否则会报错。

2、矩阵法

上仿射变换矩阵是由平移矩阵乘以缩放矩阵得到的。需要注意的是，虽然先缩放再平移，但是仿射变换矩阵是平移仿射矩阵乘以缩放仿射矩阵，而不是缩放仿射矩阵乘以平移仿射矩阵，即等式右边的运算是从右向左进行的。

对于这种等比例缩放的仿射变换，OpenCV提供了函数：cv2.getRotationMatrix2D(center, angle, scale)

3.1.5 插值算法

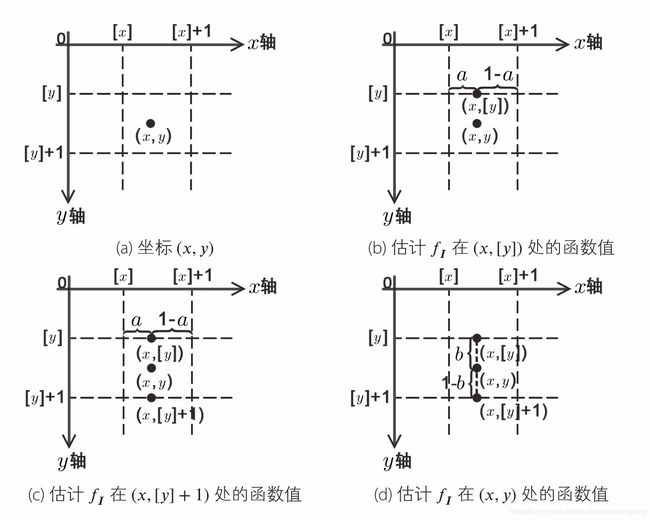
显然经过仿射变换后，有些位置坐标处的函数值是无法设置的，因此需要利用已知的整数坐标处的函数值估算非整数坐标处的函数值——插值算法。

1、最近邻插值：最近邻插值就是从（x，y）的四个相邻整数坐标中找到离它最近的一个函数值。

使用最近邻插值方法完成图像几何变换，输出图像会出现锯齿状外观，对图像放大处理的效果会更明显。

2、双线性插值：

3、高阶的插值函数，如三次样条插值、Legendre中心函数和sin（axs）函数，高阶插值常使用二维离散卷积运算来实现。

3.1.6 旋转函数Rotate

在OpenCV 3.X中通过定义函数：void rotate(InputArray src , OutputArray dst , int rotateCode) 完成图像矩阵顺时针旋转90°，180°，270°

注意：虽然是图像矩阵的旋转，但该函数不需要利用仿射变换来完成这类旋转，只是行列的互换，类似于矩阵的转置操作，所以该函数声明在头文件opencv2/core.hpp中。

3.2投影变换

在对仿射变换的讨论中，校正物体都是在二维空间中完成的，如果物体在三维空间中发生了旋转，那么这种变换通常被称为投影变换。

$\left(\begin{array}{c}{\tilde{x}} \\ {\tilde{y}} \\ {\tilde{z}}\end{array}\right)=\left(\begin{array}{ccc}{a_{11}} & {a_{12}} & {a_{13}} \\ {a_{21}} & {a_{22}} & {a_{23}} \\ {a_{31}} & {a_{32}} & {a_{33}}\end{array}\right)\left(\begin{array}{l}{x} \\ {y} \\ {z}\end{array}\right)$

与用方程法计算仿射变换矩阵的函数getAffineTransform类似，OpenCV提供了函数：

cv2.getPerspectiveTransform(src, dst) 需要提供四组对应的坐标变换；

3.3极坐标变换

通常利用极坐标变换来校正图像中的圆形物体或被包含在圆环中的物体。

1. 将笛卡儿坐标转换为极坐标

笛卡儿坐标系xoy平面上的任意一点（x，y），以为中心，通过以下计算公式对应到极坐标系θor上的极坐标（θ，r）：

$r=\sqrt{(x-\overline{x})^{2}+(y-\overline{y})^{2}}$ ， $\theta=\left\{\begin{array}{ll}{2 \pi+\arctan 2(y-\overline{y}, x-\overline{x}),} & {y-\overline{y} \leqslant 0} \\ {\arctan 2(y-\overline{y}, x-\overline{x}),} & {y-\overline{y}>0}\end{array}\right.$

OpenCV提供函数：

cartToPolar(x, y[, magnitude[, angle[, angleInDegree] ] ])实现的就是将原点移动到变换中心后的笛卡儿坐标向极坐标的变换

2. 将极坐标转换为笛卡儿坐标

极坐标变换也是可逆的，在已知极坐标（θ，r）和笛卡儿坐标的条件下，计算哪个笛卡儿坐标（x，y）以为中心的极坐标变换是（θ，r），可通过以下公式计算：

$x=\overline{x}+r \cos \theta$ , $y=\overline{y}+r \sin \theta$

来实现将极坐标转换为笛卡儿坐标，其参数解释与函数cartToPolar类似。注意：返回的是以原点（0，0）为中心的笛卡儿坐标，即已知（θ，r）和，计算出的是 $(x-\overline{x}, y-\overline{y})$ 。

OpenCV提供了函数：

cv2.polarToCart(magnitude, angle[, x[, y[, angleInDegree ] ] ])

3. 利用极坐标变换对图像进行变换

假设输入图像矩阵为I， $(\overline{x}, \overline{y})$ 代表极坐标空间变换的中心，输出图像矩阵为O，比较直观的策略是利用极坐标和笛卡儿坐标的一一对应关系得到O的每一个像素值，即

$\boldsymbol{O}(r, \theta)=f_{\boldsymbol{I}}(\overline{x}+r \cos \theta, \overline{y}+r \sin \theta)$

这里的θ和r都是以1为步长进行离散化的，由于变换步长较大，输出图像矩阵O可能会损失原图的很多信息。可以通过以下方式进行改进，假设要将与 $(\overline{x}, \overline{y})$ 的距离范围为[rmin，rmax]、角度范围在[θmin，θmax]内的点进行极坐标向笛卡儿坐标的变换，当然这个范围内的点也是无穷多的，仍需要离散化；假设r的变换步长为rstep，0<；sstep≤1，θ的变换步长为θstep，θstep一般取 $\frac{360}{180 * N}$ ，N ≥2，则输出图像矩阵的宽 $\mathrm{w} \approx\frac{r_{\max }-r_{\min }}{r_{\text { step }}}+1$ ，高 $\mathrm{h} \approx\frac{\theta_{\max }-\theta_{\min }}{\theta_{\text { step }}}+1$ 图像矩阵O的第i行第j列的值通过以下公式进行计算：

线性极坐标函数linearPolar:

void linearPolar(InputArray src, OutputArray dst, Point2f center, double maxRadius, int flags);

对数极坐标函数logPolar:

void logPolar(InputArray src , OutputArray dst, Point2f center, double M, int flags)

你可能感兴趣的:(OpenCV,OpenCV,图像处理)

Linux下QT开发的动态库界面弹出操作（SDL2） 13jjyao QT类 qt 开发语言 sdl2 linux
需求：操作系统为linux，开发框架为qt，做成需带界面的qt动态库，调用方为java等非qt程序难点：调用方为java等非qt程序，也就是说调用方肯定不带QApplication::exec()，缺少了这个，QTimer等事件和QT创建的窗口将不能弹出(包括opencv也是不能弹出)；这与qt调用本身qt库是有本质的区别的思路：1.调用方缺QApplication::exec()，那么我们在接口
tiff批量转png 诺有缸的高飞鸟 opencv 图像处理 python opencv 图像处理
目录写在前面代码完写在前面1、本文内容tiff批量转png2、平台/环境opencv,python3、转载请注明出处：https://blog.csdn.net/qq_41102371/article/details/132975023代码importnumpyasnpimportcv2importosdeffindAllFile(base):file_list=[]forroot,ds,fsin
遥感影像的切片处理 sand&wich 计算机视觉 python 图像处理
在遥感影像分析中，经常需要将大尺寸的影像切分成小片段，以便于进行详细的分析和处理。这种方法特别适用于机器学习和图像处理任务，如对象检测、图像分类等。以下是如何使用Python和OpenCV库来实现这一过程，同时确保每个影像片段保留正确的地理信息。准备环境首先，确保安装了必要的Python库，包括numpy、opencv-python和xml.etree.ElementTree。这些库将用于图像处理
Python实现下载当前年份的谷歌影像 sand&wich python 开发语言
在GIS项目和地图应用中，获取最新的地理影像数据是非常重要的。本文将介绍如何使用Python代码从Google地图自动下载当前年份的影像数据，并将其保存为高分辨率的TIFF格式文件。这个过程涉及地理坐标转换、多线程下载和图像处理。关键功能该脚本的核心功能包括：坐标转换：支持WGS-84与WebMercator投影之间转换，以及处理中国GCJ-02偏移。自动化下载：多线程下载地图瓦片，提高效率。图像
Python实现TIFF 文件转换为 PNG 和 JPG 格式 sand&wich python 开发语言
在日常的图像处理工作中，可能会遇到需要将TIFF格式的图像转换为其他格式的情况，例如PNG和JPG。下面，本文将介绍如何使用Python和GDAL库实现这一功能。准备工作在开始之前，请确保已经安装了必要的库：GDAL（GeospatialDataAbstractionLibrary）可以使用以下命令安装GDAL：pipinstallgdal代码实现以下是一个将TIFF文件转换为PNG文件的示例代码
windows下python opencv ffmpeg读取摄像头实现rtsp推流拉流图像处理大大大大大牛啊 opencv实战代码讲解视觉图像项目 windows python opencv
windows下pythonopencvffmpeg读取摄像头实现rtsp推流拉流整体流程1.下载所需文件1.1下载rtsp推流服务器1.2下载ffmpeg2.开启RTSP服务器3.opencv读取摄像头并调用ffmpeg进行推流4.opencv进行拉流5.opencv异步拉流整体流程1.下载所需文件1.1下载rtsp推流服务器下载RTSP服务器下载页面https://github.com/blu
c++ opencv4.3 sift匹配图像处理大大大大大牛啊图像处理 opencv实战代码讲解 opencv sift c++opencv4 特征点
c++opencv4.3sift匹配main.cppintmain(){vectorkeypoints1,keypoints2;Matimg1,img2,descriptors1,descriptors2;intnumF
ubuntu安装opencv最快的方法 Derek重名了
最快方法，当然不能太多文字$sudoapt-getinstallpython-opencv借助python就可以把ubuntu的opencv环境搞起来，非常快非常容易参考：https://docs.opencv.org/trunk/d2/de6/tutorial_py_setup_in_ubuntu.html
使用Python和Playwright破解滑动验证码 asfdsgdf python 开发语言
滑动验证码是一种常见的验证码形式，通过拖动滑块将缺失的拼图块对准原图中的空缺位置来验证用户操作。本文将介绍如何使用Python中的OpenCV进行模板匹配，并结合Playwright实现自动化破解滑动验证码的过程。所需技术OpenCV模板匹配：用于识别滑块在背景图中的正确位置。Python：主要编程语言。Playwright：用于浏览器自动化，模拟用户操作。破解过程概述获取验证码图像：下载背景图和
OpenCV图像处理技术（Python）——入门森屿_ opencv
©FuXianjun.AllRightsReserved.OpenCV入门图像作为人类感知世界的视觉基础，是人类获取信息、表达信息的重要手段，OpenCV作为一个开源的计算机视觉库，它包括几百个易用的图像成像和视觉函数，既可以用于学术研究，也可用于工业邻域，它于1999年由因特尔的GaryBradski启动，OpenCV库主要由C和C++语言编写，它可以在多个操作系统上运行。1.1图像处理基本操作
opencv学习：图像旋转的两种方法，旋转后的图片进行模板匹配代码实现夜清寒风学习 opencv 机器学习人工智能计算机视觉
图像旋转在图像处理中，rotate和rot90是两种常见的图像旋转方法，它们在功能和使用上有一些区别。下面我将分别介绍这两种方法，并解释它们的主要区别rot90方法rot90方法是NumPy提供的一种数组旋转函数，它主要用于对二维数组（如图像）进行90度的旋转。这个方法比较简单，只支持90度的倍数旋转，不支持任意角度旋转。使用NumPy进行旋转使用NumPy的rot90函数对模板图像进行旋转操作。
Python OpenCV图像处理：从基础到高级的全方位指南极客代码玩转Python 开发语言 python opencv 图像处理计算机视觉
目录第一部分：PythonOpenCV图像处理基础1.1OpenCV简介1.2PythonOpenCV安装1.3实战案例：图像显示与保存1.4注意事项第二部分：PythonOpenCV图像处理高级技巧2.1图像变换2.2图像增强2.3图像复原第三部分：PythonOpenCV图像处理实战项目3.1图像滤波3.2图像分割3.3图像特征提取第四部分：PythonOpenCV图像处理注意事项与优化策略4
python图像匹配_opencvpython中的图像匹配 weixin_39585675 python图像匹配
我一直在做一个项目，用opencvpython识别相机中显示的标志。我已经尝试过使用surf、颜色直方图匹配和模板匹配。但在这3个问题中，它并不总是返回正确的答案。我现在想要的是，解决我这个问题的最好办法是什么。模板图像示例：以下是摄像头中显示的标志示例。如果这是我想要识别的图像，该怎么用？在更新matchTemplate中的代码flags=["Cambodia.jpg","Laos.jpg","
利用Python+OpenCV实现截图匹配图像，支持自适应缩放、灰度匹配、区域匹配、匹配多个结果 xu-jssy Python自动化脚本 python opencv 开发语言图像处理自动化
可以直接通过pip获取，无需手动安装其他依赖pipinstallxug示例：importxugxug.find_image_on_screen(,,,)=========================================================================一、依赖安装pipinstallopencv-pythonpipinstallpyautogui二、获
服务器状态监控php源码,服务器状态监控_监控Linux服务器网站状态的SHELL脚本温糯米服务器状态监控php源码
摘要腾兴网为您分享:监控Linux服务器网站状态的SHELL脚本，蜗牛集市，同花顺，探客宝，手柄助手等软件知识，以及日期倒计时插件，云南省教育资源公共，rui手机桌面，小屁孩桌面便签，合金装备崛起复仇，朝夕日历，photoshop图像处理软件,一年级学生每日计划表，悟空找房，饿了吗外卖商家版，逃生，中国民宿网，realpolitiks，交通安全知识竞赛，雅思流利说等软件it资讯，欢迎关注腾兴网。1
opencv 学习 1 木木ainiks opencv 计算机视觉 python
opencv学习的第一天#coding:utf-8importcv2ascv#首先读图片src=cv.imread(“img/1.jpg”)#设置图片的名字cv.namedWindow(“1”,cv.WINDOW_AUTOSIZE)#显示图片第一个参数设置图片名，第二个参数图片的地址cv.imshow(“1”,src)cv.waitKey(0)#将图片写入固定位置cv.imwrite(“img/2
OpenCV结构分析与形状描述符（24）检测两个旋转矩形之间是否相交的一个函数rotatedRectangleIntersection()的使用 jndingxin OpenCV opencv 人工智能计算机视觉
操作系统：ubuntu22.04OpenCV版本：OpenCV4.9IDE:VisualStudioCode编程语言：C++11算法描述测两个旋转矩形之间是否存在交集。如果存在交集，则还返回交集区域的顶点。下面是一些交集配置的例子。斜线图案表示交集区域，红色顶点是由函数返回的。rotatedRectangleIntersection()这个函数看起来像是用于检测两个旋转矩形之间是否相交的一个方法。
python-opencv cv2.findContours()函数 fjswcjswzy opencv python笔记 python opencv
示例代码：image,contours,hierarchy=cv2.findContours(contour,cv2.RETR_TREE,cv2.CHAIN_APPROX_SIMPLE)输入：contour：带有轮廓信息的图像；cv2.RETR_TREE：提取轮廓后，输出轮廓信息的组织形式，除了cv2.RETR_TREE还有以下几种选项：cv2.RETR_EXTERNAL：输出轮廓中只有外侧轮廓信
【Python】【Opencv】cv2.findContours()、cv2.drawContours()和cv2.contourArea()函数详解和运行示例木彳 Python学习和使用过程积累 python opencv 开发语言人工智能计算机视觉
为帮助大家理解和使用cv2.findContours()、cv2.drawContours()和cv2.contourArea()函数，本文通过对函数内容进行详解，并通过运行示例更直观表述。函数解析cv2.findContours()cv2.drawContours()cv2.contourArea()运行示例运行示例示例详解函数解析cv2.findContours()cv2.findContou
python如何判断NoneTpye #如花 opencv 人工智能计算机视觉 python
python如何判断NoneTpye最近用python-opencv解析多个视频文件，解析到第一个视频的最后一帧，出现了NoneTpye报错为了让循环继续，需要判断解析出来的图片是否为NoneType。试了几种方法#第一种方法img==None当img为空时，表达式为True。但是当img解析出了图片时，返回的是一个array，大小和img一致。正确写法imgisNone用isNone判断None
多模态Transformer之文本与图像联合建模 - Transformer教程 shandianfk_com ChatGPT Transformer transformer 深度学习人工智能
大家好，今天我们来聊聊一个既前沿又有趣的话题——多模态Transformer，特别是文本与图像的联合建模。对于很多小伙伴来说，Transformer这个词已经不陌生了，但它不仅仅应用于自然语言处理，还能在图像处理、甚至是多模态数据的处理上大显身手。接下来，我会带大家深入了解什么是多模态Transformer，以及它是如何实现文本与图像的联合建模的。Transformer简介首先，我们简单回顾一下T
三点or多点的变换矩阵求解opencv & eigen 合工大机器人实验室 C++矩阵 opencv 线性代数
《Estimating3-DRigidBodyTransformations:AComparisonofFourMajorAlgorithms》，它使用SVD方法计算T和t。只要算出变换矩阵，就可以算出A坐标系的一个点P在坐标系B里的对应点坐标，即R为3x3的转换矩阵，t为3x1的位移变换向量，这里点坐标均为3x1的列向量（非齐次形式，齐次形式下为4x1列向量，多出的一个元素值补1而已）。理论上只
Matlab2024a安装教程是阿宇呢信息可视化开发语言
MATLAB是一款商业数学软件，用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境，主要包括MATLAB和Simulink两大部分，可以进行矩阵运算、绘制函数和数据、实现算法、创建用户界面、连接其他编程语言的程序等，主要应用于工程计算、控制设计、信号处理与通讯、图像处理、信号检测、金融建模设计与分析等领域。1.解压安装包：①鼠标右击【MATLABR2024a(64bit)
逆radon变换matlab,Radon变换及其Matlab代码实现少年商学院逆radon变换matlab
Radon变换和Hough变换类似，最初是用于检测图像中的直线(例如笔直的街道边沿、房屋的边沿、笔直的电线等)。关于Hough变换，可以参考OpenCV中的代码和示例(其实除了HoughLines还有HoughCircles等等变种)，此处不再赘述。关于Radon变换，可以参考wiki或者百科，或者网络上的其他资料介绍。这里做一个简单的总结。首先准备一张灰度化的图像，及黑白图像，然后检测图像的边缘
ubuntu opencv 安装科学的发展-只不过是读大自然写的代码 opencv基础 ubuntu opencv linux
1.ubuntuopencv安装在Ubuntu系统中安装OpenCV，可以通过多种方式进行，以下是一种常用的安装方法，包括从源代码编译安装。请注意，安装步骤可能会因OpenCV的版本和Ubuntu系统的具体版本而略有不同。一、安装准备更新系统（确保你的Ubuntu系统是最新的）：sudoaptupdatesudoaptupgrade安装必要的依赖项：sudoaptinstallbuild-esse
结合YOLOv8和OpenCV WeChat QRCode打造一款二维码识别器搜狐技术产品小编2023 YOLO opencv 微信人工智能计算机视觉
本文字数：3876字预计阅读时间：25分钟01引言二维码（QRCode）在现代生活中有广泛应用，从支付系统到信息传递，它们无处不在。本文提出了一种如何识别二维码的方法，主要贡献在于优化处理分辨率较高的图像时，由于二维码在整张图片中占据的比例较小，传统的OpenCVWeChatQRCode的识别方法表现不佳的问题。下面描述详细的优化过程。02OpenCVWeChatQRCodeWeChatQRCod
图像处理的作用（6幅图诗）静月园
静月园著2020年1月️4日1自然力出现的图形画面，即无序，又有形。奇妙令人联想无限。好象理石花纹，又类似草木树植。2为何要如此色彩？好奇怪哦！自然的物态鬼斧神工。3孩童们信手涂鸦，但是脑控制了手的动作，所绘画的物体形状代表了孩子们对环境人物的所看，所听，所理解的形状。脑的心理活动影像，被转换成手的动作输出到笔尖的移动动作上，于是我们看到了简单的结构形状图。而对于我们的写作者来说，我们的作家脑内有
OpenCV高阶操作富士达幸运星 opencv 人工智能计算机视觉
在图像处理与计算机视觉领域，OpenCV（OpenSourceComputerVisionLibrary）无疑是最为强大且广泛使用的工具之一。从基础的图像读取、1.图片的上下，采样下采样（Downsampling）下采样通常用于减小图像的尺寸，从而减少图像中的像素数。这个过程可以通过多种方法实现，但最常见的是通过图像金字塔中的pyrDown函数（在OpenCV中）或其他类似的滤波器（如平均池化、最
Vue + Django的人脸识别系统 DXSsssss python DRF tensorflow 人脸识别
最近在研究机器学习，刚好最近看了vue+Djangodrf的一些课程，学以致用，做了一个人脸识别系统。项目前端使用Vue框架，用到了elementui组件，写起来真是方便。比之前传统的dtl方便了太多。后端使用了drf，识别知识刚开始打算使用opencv+tensorflow,但是发现吧识别以后的结果返回到浏览器当中时使用opencv比较麻烦（主要是我太菜，想不到比较好的方法），因此最终使用了tf
Django+Vue基于OpenCV的人脸识别系统的设计与实现赵广陆 project django vue.js opencv
目录1项目介绍2项目截图3核心代码3.1需要的环境3.2Django接口层3.3实体类3.4config.ini3.5启动类3.5Vue4数据库表设计5文档参考6计算机毕设选题推荐7源码获取1项目介绍博主个人介绍：CSDN认证博客专家，CSDN平台Java领域优质创作者，全网30w+粉丝，超300w访问量，专注于大学生项目实战开发、讲解和答疑辅导，对于专业性数据证明一切！主要项目：javaweb、
异常的核心类Throwable 无量 java 源码异常处理 exception
java异常的核心是Throwable，其他的如Error和Exception都是继承的这个类里面有个核心参数是detailMessage，记录异常信息，getMessage核心方法，获取这个参数的值，我们可以自己定义自己的异常类，去继承这个Exception就可以了，方法基本上，用父类的构造方法就OK，所以这么看异常是不是很easy package com.natsu;
mongoDB 游标（cursor）实现分页迭代开窍的石头 mongodb
上篇中我们讲了mongoDB 中的查询函数，现在我们讲mongo中如何做分页查询如何声明一个游标 var mycursor = db.user.find({_id:{$lte:5}}); 迭代显示游标数
MySQL数据库INNODB 表损坏修复处理过程 0624chenhong tomcat mysql
最近mysql数据库经常死掉，用命令net stop mysql命令也无法停掉，关闭Tomcat的时候，出现Waiting for N instance(s) to be deallocated 信息。查了下，大概就是程序没有对数据库连接释放，导致Connection泄露了。因为用的是开元集成的平台，内部程序也不可能一下子给改掉的，就验证一下咯。启动Tomcat,用户登录系统，用netstat -
剖析如何与设计人员沟通不懂事的小屁孩工作
最近做图烦死了，不停的改图，改图……。烦，倒不是因为改，而是反反复复的改，人都会死。很多需求人员不知该如何与设计人员沟通，不明白如何使设计人员知道他所要的效果，结果只能是沟通变成了扯淡，改图变成了应付。那应该如何与设计人员沟通呢？我认为设计人员与需求人员先天就存在语言障碍。对一个合格的设计人员来说，整天玩的都是点、线、面、配色，哪种构图看起来协调；哪种配色看起来合理心里跟明镜似的，
qq空间刷评论工具换个号韩国红果果 JavaScript
var a=document.getElementsByClassName('textinput'); var b=[]; for(var m=0;m<a.length;m++){ if(a[m].getAttribute('placeholder')!=null) b.push(a[m]) } var l
S2SH整合之session 灵静志远 spring AOP struts session
错误信息： Caused by: org.springframework.beans.factory.BeanCreationException: Error creating bean with name 'cartService': Scope 'session' is not active for the current thread; consider defining a scoped
xmp标签 a-john 标签
今天在处理数据的显示上遇到一个问题： var html = '<li><div class="pl-nr"><span class="user-name">' + user + '</span>' + text + '</div></li>'; ulComme
Ajax的常用技巧（2）---实现Web页面中的级联菜单 aijuans Ajax
在网络上显示数据，往往只显示数据中的一部分信息，如文章标题，产品名称等。如果浏览器要查看所有信息，只需点击相关链接即可。在web技术中，可以采用级联菜单完成上述操作。根据用户的选择，动态展开，并显示出对应选项子菜单的内容。在传统的web实现方式中，一般是在页面初始化时动态获取到服务端数据库中对应的所有子菜单中的信息，放置到页面中对应的位置，然后再结合CSS层叠样式表动态控制对应子菜单的显示或者隐
天-安-门，好高 atongyeye 情感
我是85后，北漂一族，之前房租1100，因为租房合同到期，再续，房租就要涨150。最近网上新闻，地铁也要涨价。算了一下，涨价之后，每次坐地铁由原来2块变成6块。仅坐地铁费用，一个月就要涨200。内心苦痛。晚上躺在床上一个人想了很久，很久。我生在农
android 动画百合不是茶 android 透明度平移缩放旋转
android的动画有两种 tween动画和Frame动画 tween动画;,透明度,缩放,旋转,平移效果 Animation 动画 AlphaAnimation 渐变透明度 RotateAnimation 画面旋转 ScaleAnimation 渐变尺寸缩放 TranslateAnimation 位置移动 Animation
查看本机网络信息的cmd脚本 bijian1013 cmd
@echo 您的用户名是：%USERDOMAIN%\%username%>"%userprofile%\网络参数.txt" @echo 您的机器名是：%COMPUTERNAME%>>"%userprofile%\网络参数.txt" @echo ___________________>>"%userprofile%\
plsql 清除登录过的用户征客丶 plsql
tools---preferences----logon history---history 把你想要删除的删除 -------------------------------------------------------------------- 若有其他凝问或文中有错误，请及时向我指出，我好及时改正，同时也让我们一起进步。 email ： binary_spac
【Pig一】Pig入门 bit1129 pig
Pig安装 1.下载pig wget http://mirror.bit.edu.cn/apache/pig/pig-0.14.0/pig-0.14.0.tar.gz 2. 解压配置环境变量如果Pig使用Map/Reduce模式，那么需要在环境变量中，配置HADOOP_HOME环境变量 expor
Java 线程同步几种方式 BlueSkator volatile synchronized ThredLocal ReenTranLock Concurrent
为何要使用同步？ java允许多线程并发控制，当多个线程同时操作一个可共享的资源变量时（如数据的增删改查），将会导致数据不准确，相互之间产生冲突，因此加入同步锁以避免在该线程没有完成操作之前，被其他线程的调用，从而保证了该变量的唯一性和准确性。 1.同步方法&
StringUtils判断字符串是否为空的方法（转帖） BreakingBad null StringUtils “”
转帖地址：http://www.cnblogs.com/shangxiaofei/p/4313111.html public static boolean isEmpty(String str) 　　判断某字符串是否为空，为空的标准是 str== null 或 str.length()== 0
编程之美-分层遍历二叉树 bylijinnan java 数据结构算法编程之美
import java.util.ArrayList; import java.util.LinkedList; import java.util.List; public class LevelTraverseBinaryTree { /** * 编程之美分层遍历二叉树 * 之前已经用队列实现过二叉树的层次遍历，但这次要求输出换行，因此要
jquery取值和ajax提交复习记录 chengxuyuancsdn jquery取值 ajax提交
// 取值 // alert($("input[name='username']").val()); // alert($("input[name='password']").val()); // alert($("input[name='sex']:checked").val()); // alert($("
推荐国产工作流引擎嵌入式公式语法解析器-IK Expression comsci java 应用服务器工作 Excel 嵌入式
这个开源软件包是国内的一位高手自行研制开发的，正如他所说的一样，我觉得它可以使一个工作流引擎上一个台阶。。。。。。欢迎大家使用，并提出意见和建议。。。 ----------转帖--------------------------------------------------- IK Expression是一个开源的（OpenSource），可扩展的（Extensible），基于java语言
关于系统中使用多个PropertyPlaceholderConfigurer的配置及PropertyOverrideConfigurer daizj spring
1、PropertyPlaceholderConfigurer Spring中PropertyPlaceholderConfigurer这个类，它是用来解析Java Properties属性文件值，并提供在spring配置期间替换使用属性值。接下来让我们逐渐的深入其配置。基本的使用方法是：(1) <bean id="propertyConfigurerForWZ&q
二叉树:二叉搜索树 dieslrae 二叉树
所谓二叉树,就是一个节点最多只能有两个子节点,而二叉搜索树就是一个经典并简单的二叉树.规则是一个节点的左子节点一定比自己小,右子节点一定大于等于自己(当然也可以反过来).在树基本平衡的时候插入,搜索和删除速度都很快,时间复杂度为O(logN).但是,如果插入的是有序的数据,那效率就会变成O(N),在这个时候,树其实变成了一个链表. tree代码:
C语言字符串函数大全 dcj3sjt126com c function
C语言字符串函数大全函数名: stpcpy 功能: 拷贝一个字符串到另一个用法: char *stpcpy(char *destin, char *source); 程序例: #include <stdio.h> #include <string.h> int main
友盟统计页面技巧 dcj3sjt126com 技巧
在基类调用就可以了, 基类ViewController示例代码 -(void)viewWillAppear:(BOOL)animated { [super viewWillAppear:animated]; [MobClick beginLogPageView:[NSString stringWithFormat:@"%@",self.class]];
window下在同一台机器上安装多个版本jdk，修改环境变量不生效问题处理办法 flyvszhb java jdk
window下在同一台机器上安装多个版本jdk，修改环境变量不生效问题处理办法本机已经安装了jdk1.7，而比较早期的项目需要依赖jdk1.6，于是同时在本机安装了jdk1.6和jdk1.7. 安装jdk1.6前，执行java -version得到 C:\Users\liuxiang2>java -version java version "1.7.0_21&quo
Java在创建子类对象的同时会不会创建父类对象 happyqing java 创建子类对象父类对象
1.在thingking in java 的第四版第六章中明确的说了，子类对象中封装了父类对象， 2."When you create an object of the derived class, it contains within it a subobject of the base class. This subobject is the sam
跟我学spring3 目录贴及电子书下载 jinnianshilongnian spring
一、《跟我学spring3》电子书下载地址：《跟我学spring3》（1-7 和 8-13） http://jinnianshilongnian.iteye.com/blog/pdf 跟我学spring3系列 word原版下载二、源代码下载最新依
第12章 Ajax（上） onestopweb Ajax
index.html <!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd"> <html xmlns="http://www.w3.org/
BI and EIM 4.0 at a glance blueoxygen BO
http://www.sap.com/corporate-en/press.epx?PressID=14787 有机会研究下EIM家族的两个新产品~~~~ New features of the 4.0 releases of BI and EIM solutions include: Real-time in-memory computing –
Java线程中yield与join方法的区别 tomcat_oracle java
长期以来，多线程问题颇为受到面试官的青睐。虽然我个人认为我们当中很少有人能真正获得机会开发复杂的多线程应用(在过去的七年中，我得到了一个机会)，但是理解多线程对增加你的信心很有用。之前，我讨论了一个wait()和sleep()方法区别的问题，这一次，我将会讨论join()和yield()方法的区别。坦白的说，实际上我并没有用过其中任何一个方法，所以，如果你感觉有不恰当的地方，请提出讨论。 &nb
android Manifest.xml选项阿尔萨斯 Manifest
结构继承关系 public final class Manifest extends Objectjava.lang.Objectandroid.Manifest 内部类 class Manifest.permission权限 class Manifest.permission_group权限组构造函数 public Manifest () 详细 androi
Oracle实现类split函数的方 zhaoshijie oracle
关键字：Oracle实现类split函数的方项目里需要保存结构数据，批量传到后他进行保存，为了减小数据量，子集拼装的格式，使用存储过程进行保存。保存的过程中需要对数据解析。但是oracle没有Java中split类似的函数。从网上找了一个，也补全了一下。 CREATE OR REPLACE TYPE t_split_100 IS TABLE OF VARCHAR2(100); cr

按字母分类： A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 其他