欧拉图（欧拉回路与欧拉通路）

在一个图中（有向图或无向图），如果能够从一个结点出发一次性通过所有边且每条边只能通过一次，在通过所有边后能够回到出发点，则该回路称为该图的欧拉回路；不能回到出发点，则该通路称为欧拉通路。含有欧拉回路的图称为欧拉图，含欧拉通路的称为半欧拉图。

最简单的欧拉图：

最简单的半欧拉图：

如何用算法得到一张有向图的欧拉通路呢（无向图算法类似）？我们来看下面这张图：



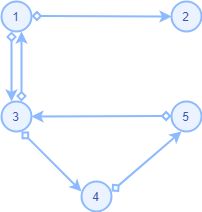
假设1是起点，则有效的欧拉通路是1–>3–>4–>5–>3–>1–>2；看似我们只需要用最普通的DFS算法（DFS图的搜索算法点击这里）就可以实现，但实际上走出一条有效的欧拉通路还是有一定限制的——当我们处于起点位置：结点1时，我们只能选择走结点3而不能选择走结点2，因为结点2是一条死路，不能遍历图的所有边，所以由此可以得出，我们在设计算法寻找欧拉通路时，要注意走到死路的情况。
认真分析欧拉通路的走法我们可以发现，如果一张图是半欧拉图，则这张图最多有一条死路（一条死路是不能到达另一条死路的），而且这条死路一定是最后走的那条路，所以我们可以这样设计算法（找欧拉回路可以也可以用这一算法）：

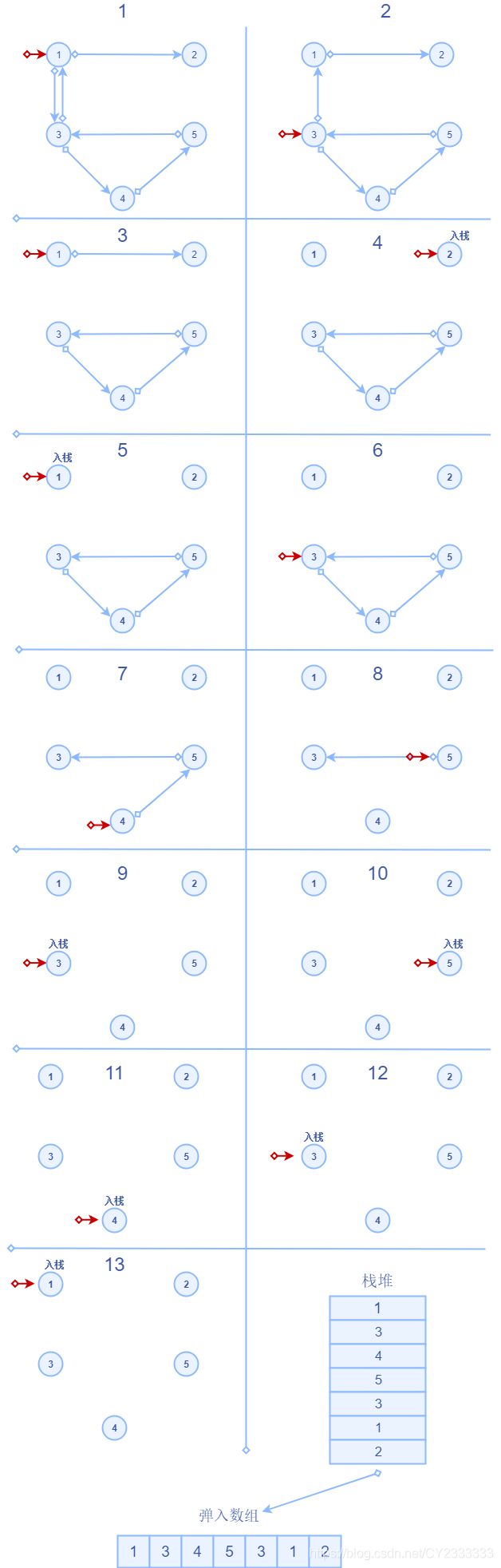
Hierholzer算法——1.从起点出发，进行深度优先搜索，同时维护一个栈。

2.每次沿着某条边从某个顶点移动到另外一个顶点的时候，都需要删除这条边。

3.如果所在结点已经没有可移动的路径，则将所在节点加入到栈中。

4.当所有结点入栈后，将栈弹入结果数组中（倒置），则可以得到这条欧拉通路）

图解：

Java代码：
这是一道leetcode的题解，用了上文介绍的Hierholzer算法，看题目点击这里

import java.util.*;
//Hierholzer算法
class Solution {
     
    //数组list直接代替栈堆，可简化计算，但是使用栈更有利于理解算法
    List<String> list=new ArrayList<>();
    //map用于存储图的信息
    HashMap<String,Queue<String>>map=new HashMap<>();
    public List<String> findItinerary(List<List<String>> tickets) {
     
        for(List<String> x:tickets) {
     
            String Pos = x.get(0);
            String next = x.get(1);
            if (!map.containsKey(Pos))
                map.put(Pos, new PriorityQueue<>(new Comparator<String>() {
     
                    @Override
                    public int compare(String o1, String o2) {
     
                        return o1.compareTo(o2);
                    }
                }));
            map.get(Pos).offer(next);
        }
        //开始DFS递归搜索
        DFS("JFK");
        //反转数组，得到欧拉通路的正确顺序
        Collections.reverse(list);
        return list;
    }
    //DFS递归
    private void DFS(String curr){
     
        //直到所在结点没有出边时，才跳出while循环，加入数组
        while(map.containsKey(curr)&&map.get(curr).size()>0){
     
            String temp=map.get(curr).poll();
            DFS(temp);
        }
        list.add(curr);
    }

}