高斯玻色采样enhance量子近似优化算法
上篇博文,我们已经接触了QAOA量子近似优化算法,我们已经知道近似优化算法一般用于求解组合优化问题。这里我们再说明一下什么是组合优化问题:
给定一个数据集 X = { x 1 , x 2 , . . . x N } X={{x_{1},x_{2},...x_{N}}} X={x1,x2,...xN},和一个映射函数 f f f,令 y i = f ( x i ) y_{i}=f(x_{i}) yi=f(xi), Y = { y 1 , y 2 , . . . y N } Y={{y_{1},y_{2},...y_{N}}} Y={y1,y2,...yN},目标是找到一个元素 x ∗ ∈ X x^{*}\in X x∗∈X,使得 f ( x ∗ ) > f ( x ) , x ∈ X f(x^{*})>f(x),x\in X f(x∗)>f(x),x∈X,即找到最大的一个 y y y.
这篇博文,打算就依照参考论文[1]的步骤一步步的为大家解读,如果在解读过程中有问题欢迎大家评论。希望我们都能够共同进步,努力成为一名合格的科研dog。
注:量子近似优化算法有很多种,解读论文中将场景设定在随机优化算法里面。(笔者认为,对于解可以用向量或者矩阵表示的问题,可以采用随机优化的算法来求近似最优解。)
技术总结
这篇论文,意在突出Gaussian boson sampling在随机优化问题上的优势——在解决Max-Haf的问题上,通用方法(模拟退火、贪婪算法)使用的是统一采样,作者将基于GBS的比例采样应用到这两种方法上,证明了GBS 比例采样的天然优势。因为据作者分析,经过GBS比例采样得到子矩阵,更有可能计算出Max-Haf值。具体推到请看下文~
玻色采样
至今,提出的玻色采样装置有很多种,包括scattershot boson sampling 和 Gaussian boson sampling. 玻色采样的概念是在2014年被首次提出,其具体过程可以描述如下:
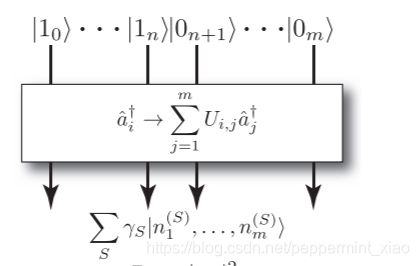
其中输入端可以是玻色子 ∣ 1 0 ⟩ . . . ∣ 0 m ⟩ |1_{0}\rangle...|0_{m}\rangle ∣10⟩...∣0m⟩,然后经过线性光学网络 U U U的作用,可以输出各种玻色配置。在光子探测器未探测光子之前,各种输出配置会处于叠加状态,其Hilbert空间可以达到 ( n m + n − 1 ) \left( \begin{array}{c} n \\ m+n-1 \\ \end{array} \right) (nm+n−1)大小, m m m是模数, n n n表示光子数。当然对于Gaussian boson sampling来说,输入端输入的不是玻色子,而是Gaussian state。
由于玻色采样装置输出配置的概率分布和积和式(NP-Hard问题)有关,因此在经典计算机上很难以模拟出来。所以玻色采样可能具有量子霸权的前景,但是在实际应用中似乎还没有崭露头角。
玻色采样的概率分布之所以经典难以模拟,是因为概率分布涉及到超高复杂度的计算。对于玻色采样,其配置概率计算涉及矩阵积和式(Permanent);对于高斯玻色采样,其配置概率计算涉及矩阵Hafinian。这两者,前者是经典NP-Hard问题,后者是经典#P-Hard问题。我们可以看下,Permanent和Hafinian定义是什么样子的:
给定矩阵 X 2 m ∗ 2 m X_{2m*2m} X2m∗2m,其积和式和Hafinian计算分别如下:
-
Permanent
P e r ( X 2 m ∗ 2 m ) = ∑ σ ∈ P E P 2 m ∏ j = 1 2 m x j , σ j Per(X_{2m*2m})=\sum_{\sigma\in PEP_{2m}}\prod_{j=1}^{2m}x_{j,\sigma_{j}} Per(X2m∗2m)=∑σ∈PEP2m∏j=12mxj,σj -
Hafinian
H a f ( X 2 m ∗ 2 m ) = ∑ σ ∈ P E P 2 m ∏ j = 1 m x σ 2 j − 1 , σ 2 j Haf(X_{2m*2m})=\sum_{\sigma\in PEP_{2m}}\prod_{j=1}^{m}x_{\sigma_{2j-1},\sigma_{2j}} Haf(X2m∗2m)=∑σ∈PEP2m∏j=1mxσ2j−1,σ2j
其中 P E P 2 m PEP_{2m} PEP2m表示的是元素 1 , 2 , . . . , 2 m {1,2,...,2m} 1,2,...,2m的全排列形成的集合。
当m=2时,
P e r ( X 4 ∗ 4 ) = ∑ σ ∈ P E P 4 ∏ j = 1 4 x j , σ j = ∑ σ ∈ P E P 4 x 1 , σ 1 x 2 , σ 2 x 3 , σ 3 x 4 , σ 4 Per(X_{4*4})=\sum_{\sigma\in PEP_{4}}\prod_{j=1}^{4}x_{j,\sigma_{j}}=\sum_{\sigma\in PEP_{4}}x_{1,\sigma_{1}}x_{2,\sigma_{2}}x_{3,\sigma_{3}}x_{4,\sigma_{4}} Per(X4∗4)=∑σ∈PEP4∏j=14xj,σj=∑σ∈PEP4x1,σ1x2,σ2x3,σ3x4,σ4
H a f ( X 4 ∗ 4 ) = ∑ σ ∈ P E P 4 ∏ j = 1 2 x σ 2 j − 1 , σ 2 j = ∑ σ ∈ P E P 4 x σ 1 , σ 2 x σ 3 , σ 4 Haf(X_{4*4})=\sum_{\sigma\in PEP_{4}}\prod_{j=1}^{2}x_{\sigma_{2j-1},\sigma_{2j}}=\sum_{\sigma\in PEP_{4}}x_{\sigma_{1},\sigma_{2}}x_{\sigma_{3},\sigma_{4}} Haf(X4∗4)=∑σ∈PEP4∏j=12xσ2j−1,σ2j=∑σ∈PEP4xσ1,σ2xσ3,σ4
从公式中可以看出,Per的复杂度计算是高于Haf的,即NP-Hard得计算难度难于#P-Hard问题。
玻色采样的理念就补充到这里了,如果没有理解的伙伴,可以多多查找一些文献,比如文献[2]。
统一采样和比例采样
-
统一采样(uniform samples)
每个值 x i x_{i} xi被采样的概率均为 1 / N 1/N 1/N,即 P U ( x i ) = 1 / N P_{U}{(x_{i})}=1/N PU(xi)=1/N.那么总目标值 Y Y Y的期望值为:
E ( Y ) = ∑ i = 1 N y i P ( y i ) = ∑ i = 1 N y i ∗ 1 / N = ∥ y ∥ 1 N E(Y)=\sum_{i=1}^{N}y_{i}P(y_{i})=\sum_{i=1}^{N}y_{i}*1/N=\frac{\|y\|_{1}}{N} E(Y)=∑i=1NyiP(yi)=∑i=1Nyi∗1/N=N∥y∥1. -
比例采样
每个值 x i x_{i} xi被采样的概率和目标值 y i y_{i} yi在总目标值的概率相等,即 P ( x i ) = y i ∑ i = 1 N y i P(x_{i})=\frac{y_{i}}{\sum_{i=1}^{N}y_{i}} P(xi)=∑i=1Nyiyi,所以总目标值 Y Y Y的期望值为:
E ( Y ) = ∑ i = 1 N y i P ( y i ) = ∑ i = 1 N y i y i ∑ i = 1 N y i = ( ∥ y ∥ 2 ) 2 ∥ y 1 ∥ E(Y)=\sum_{i=1}^{N}y_{i}P(y_{i})=\sum_{i=1}^{N}y_{i}\frac{y_{i}}{\sum_{i=1}^{N}y_{i}}=\frac{(\|y\|_{2})^{2}}{\|y_{1}\|} E(Y)=∑i=1NyiP(yi)=∑i=1Nyi∑i=1Nyiyi=∥y1∥(∥y∥2)2.
因为:
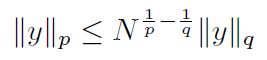
其中 p < q p< q p<q.所以:
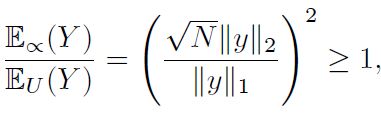
这个不等式说明了,比例采样永远不会比统一采样要差。而Gaussian boson sampling属于比例采样。
Gaussian玻色采样求解Max-Haf问题
-
The Max-Haf Problem
定义如下:
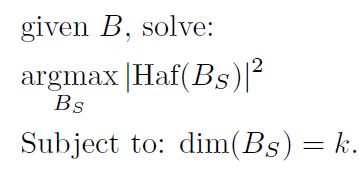
其中B是unitary矩阵,对应于高斯玻色采样装置中的光学线性网络。 B S B_{S} BS是B根据配置 S S S所得到的子矩阵。
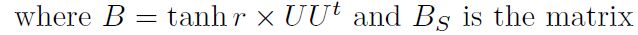
Gaussian玻色采样对应的配置 S S S,指的是可能的输出结果,如下, s i ∈ 0 , 1 s_{i} \in {0,1} si∈0,1代表输出端口有0个光子或者1个光子。
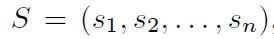
那么,配置 S S S的概率函数为:
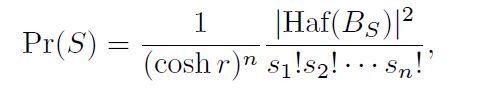
可以设想,如果得到的某个配置 S S S概率越高,也就说明子矩阵 H a f ( B S ) Haf(B_{S}) Haf(BS)越大,同时也可以求出其值。对于经典计算机,可能要花极大的计算量来计算的Haf值,利用Gaussian boson sampling就可以通过简单地比例采样(这里我认为是,Gaussian boson sampling的输出其实就是一种比例采样得到的结果,哪个占比比较多,对应的结果输出的概率也就越大)来求出相应的值。
但是,我们会有疑问,难道经典计算机就不可以使用采样的方法来计算矩阵的Haf值吗?答案其实是可以的,但是由于没有先验知识,我们并不知道哪些采样可以使得矩阵获得Max-Haf,所以在经典计算机上,一般使用uniform sampling。
然后Arrazola等人,就在基于GBS的比例采样和统一采样之间进行了比较:
给定一个symmertric Gaussian random matricx X X X
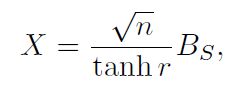
-
uniform sampling得到的 ∣ H a f ( B S ) ∣ 2 |Haf(B_{S})|^{2} ∣Haf(BS)∣2期望计算如下:
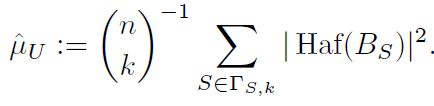
-
GBS sampling得到的 ∣ H a f ( B S ) ∣ 2 |Haf(B_{S})|^{2} ∣Haf(BS)∣2期望计算如下:
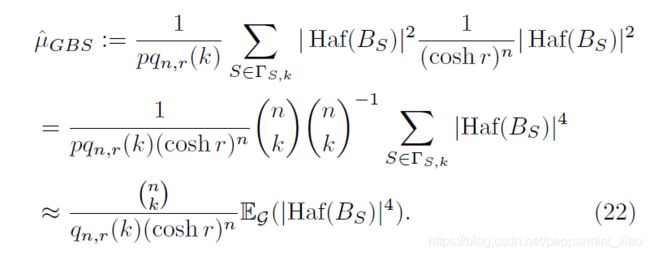
作者通过两者之间的最终比值:
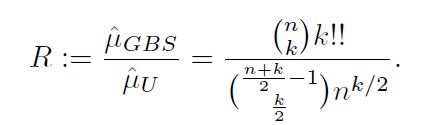
发现对于所有的 k > = 2 k>=2 k>=2,GBS sampling 下的Max-Haf比uniform sampling下的要更大概率出现,即所得到的 ∣ H a f ( B S ) ∣ 2 |Haf(B_{S})|^{2} ∣Haf(BS)∣2期望值更大一点。随着光子数 k k k的增多,这种优势会更加明显。
在随机优化算法中,会在两种方法中应用随机性:exploration 和tweaking。
什么是exploration?
在随机优化算法里面,通常会执行这个步骤来随即均匀地选择子矩阵,即选择认为是一些好的子矩阵;在GBS-Max-Haf这个例子里,则是对应到随机地选择一组子矩阵 B S B_{S} BS。
什么是tweaking?
可以随机修改样本,并生成一个新的样本;在GBS-Max-Haf这个例子中,因为要保证光子数 k k k不变,所以只能改变配置 S S S中非零序列的位置
作者定义了GBS如何在exploration和tweaking中的使用:
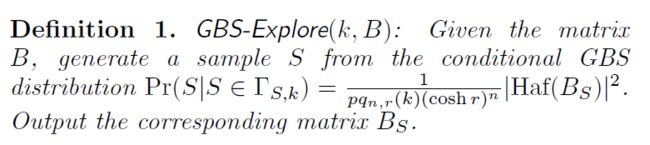

G B S − − E x p l o r e ( k , B ) GBS--Explore(k,B) GBS−−Explore(k,B)的定义是比较好理解的:就是在条件GBS分布下,采样得到一个子矩阵 B S B_{S} BS.
G B S − T w e a k ( S , ℓ , B ) GBS-Tweak(S,\ell,B) GBS−Tweak(S,ℓ,B)的定义:首先是生成了带有 ℓ + L \ell+L ℓ+L个1的二进制序列 S ′ S^{'} S′;
然后生成了带有 L L L个1的二进制序列 T ′ T^{'} T′。而且 S ′ S^{'} S′和 T ′ T^{'} T′之间,1的位置不会有重叠;最后得到带有 k ′ ( < = k ) k^{'}(<=k) k′(<=k)个1的二进制序列 R = S ′ + T ′ R=S^{'}+T^{'} R=S′+T′(这也就是为什么 S ′ S^{'} S′和 T ′ T^{'} T′之间不能有重叠的原因),其中 ℓ ∈ 0 , 2 , 4... , k − 2 \ell \in{0,2,4...,k-2} ℓ∈0,2,4...,k−2, L ∈ 0 , 1 , . . . , k − ℓ − 1 L\in{0,1,...,k-\ell-1} L∈0,1,...,k−ℓ−1。
接下来,作者给出了基于GBS求解Max-Haf的两种随机优化算法:simulated annealing 和 greedy algorithms。
Discussion
即,是否可以通过机器学习来为子矩阵优化以外的问题,生成比例分布。
思考:还能不能为GBS找到求解Max-Haf问题,以外的随机优化算法上的应用呢?同文作者,又研究了一篇利用GBS enhance 寻找密集子图问题上[3].
[1]Arrazola J M, Bromley T R, Rebentrost P. Quantum approximate optimization with Gaussian boson sampling[J]. Physical Review A, 2018, 98(1): 012322.
[2]Gard B T, Motes K R, Olson J P, et al. An introduction to boson-sampling[M]//From atomic to mesoscale: The role of quantum coherence in systems of various complexities. 2015: 167-192.
[3]J. M. Arrazola and T. R. Bromley, Physical Review Letters 121, 030503 (2018).


