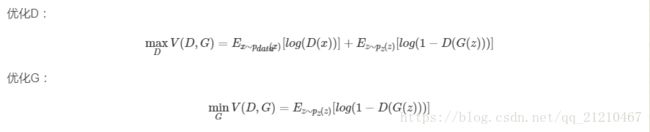生成对抗网络GANs(笔记二)代码
一、概述
生成对抗网络(GAN,Generative Adversatial Networks)作为一种学习模型,是近年来无监督学习上最具前景的方法之一。被Yann Lecun 赞叹 GAN 是机器学习近十年来最有意思的想法。
生成器(Generative model):看做一个样本生成器,它接受一个噪声信号作为输入,在经过一系列处理变成一个模拟样本。
判别器(Discrimination model):看做一个二元分类器,接受真实样本x和模拟样本x',将真实样本作为概率1输出,模拟样本作为0输出。
训练过程:生成器和判别器的博弈过程,过程和其它网络的训练差不多,都是向着梯度下降的方向优化代价函数,训练结果是两者达到纳什均衡。这个时候生成器生成的模拟样本和真实样本已经看不出差异,所以经过判别器的时候,判别器无法判断出他的输入时真实样本还是模拟样本。
GAN是要干什么?
嗯,假设我们有一堆数据,这些数据没有标签,比如我们有一堆的人脸图片,各种人脸,都不知道谁是谁,只是有一堆的脸。然后我们想要通过这一堆数据生成新的数据(原始的论文做的工作),如上图:目标是利用一个输入的噪声信号模拟得到一些人脸数据,这些生成的数据和原有数据很相似,人眼无法看出来区别。论文里面Generative Adversarial Net讲的假币的例子真是形象生动:一个造假币的团队(生成器)和抓造假的警察(判别器),一开始造假币的团队造假技术不过关,所以造出的假币总是被警察看穿,在这个过程中他们就要不停的提升自己的造假水平以避免被抓,而警察一开始可以很轻易的就判断出假币。但是随着团队造假技术的不断提高,警察可能都判断不出来是真币还是假币,所以警察也要在这个过程中不断提高自己的判断水平。最后造假团队的技术上升到了一个高度,同时警察的判断能力也达到了一定的高度,但是,造假团队的假币警察都判断不出来真假了。即0.5的几率判断出来是假币,0.5的几率判断出是真币。那么我们训练的目的就达到了。这就是一个双人博弈!
看过论文的都应该认识下面的几个公式:
详细:设J(D)是一个判别网络的目标函数——一个交叉熵(cross entropy)函数,J(D(x))左边的部分D(x)表示判断出x是真x的情况,右边部分表示D判别出有生成网络G把噪声数据z给为造出来的情况。J(G)表示生成网络的目标函数,他的目的是和D反着干,所以在前面加了负号,类似一个Jensen-Shannon(JS)距离。
GAN的优化目标有两个:优化判别器D和和优化生成器G,将第一个公式拆两个部分,注意D()代表的是网络判断图片是否真实的概率:
1、优化判别器D的时候,我们希望D的鉴别能力可以达到最大,而log函数是一个单调递增函数,所以指数最大就好了。所以D(x)最大而(1-D(G(z)))也要最大(即D(G(z))最小),等于是说D能判断出来输入是来自于生成模型G。优化G的时候,我们要让G最小,看公式的第一项,没有涉及G,所可看做常数项忽略就好,只需要优化后面的部分,这时的G(z)应该是接近真实样本的即D(G(z))最大。最小和最大自然的就产生了博弈,最终的结果是判别器的判别能力从1慢慢降到了0.5。这就是我们要找的均衡点(纳什均衡)也就是J(D)的鞍点(saddle point)
有公式来解释:
对于D:
如图,黑色点是真实数据data;绿色线是模型生成的伪数据model,是由映射过去的。蓝色的线是我们要学习的D,它的目的是要把data和model的分布区分开,谢伟公式就是data和model分布相加做分母,分子是真是的data分布。最终的效果是D无线接近于1/2 = 0.5。也就是说Pdata和Pmodel无限相似,D再也无法辨别真伪数据的区别。最终的结果如下图:
但是一个问题就是:达到这样的结果之后,生成模型就没有办法再学习了。因为1/2的导数永远是0。
为了解决这个问题,除了把两者对抗做成最小最大博弈,还可以把它写成非饱和(Non-Saturating)博弈:
也就是说用G自己的伪装成功率来表示自己的目标函数(不再是直接拿J(D) 的负数)。这样的话,我们的均衡就不再是由损失(loss)决定的了。J(D) 跟J(G) 没有简单粗暴的相互绑定,就算在D完美了以后,G还可以继续被优化。
代码:这里的例子是模拟论文中生成的高斯分布。
地址:https://github.com/MrRenQIANG/GANs
关键代码解析:
1、感知机部分,将随机噪声转换成适合判别器输入的维度。
2、指数衰减的学习率,以及动量优化方法:
3、使用均方误差的判别器预训练
4、网络结构以及整体的优化函数
5、训练和结果
6、对抗过程中,D,G的变化趋势
Reference:
http://c.m.163.com/news/a/C7UE2MLT0511AQHO.html?spss=newsapp&spsw=1