图像旋转平移、仿射变换、透视变换
目录
- 写在前面
- 本文内容
- 1、图像的旋转平移
-
- 二维xy坐标系
-
- 旋转
- 图像坐标系
-
- 旋转
- 旋转平移
- 旋转平移缩放
- 特殊情况
- 2、单应性变换
-
- 仿射变换
- 透视变换
- 3、opencv实验
-
- 图像的旋转平移缩放实现
-
- 代码
- 不作任何变换
- 平移
- 平移+旋转
- 仿射(用不同的缩放系数进行缩放)
- 透视
- 坐标系变换与图像坐标变换
- 完
写在前面
1、文中所有资源、参考已给出来源链接,如有侵权请联系删除
2、码字不易,转载本文请注明出处,本文链接:https://blog.csdn.net/qq_41102371/article/details/116245483
3、本文实验环境:win10+vs2019+opencv440(vs2019配置opencv+contrib-440 + PCL1.10.0 + 源码单步调试https://blog.csdn.net/qq_41102371/article/details/108727224)
本文内容
1、图像的旋转平移原理及其实现
2、仿射变换及实例
3、透视变换及实例
4、opencv实验结果
1、图像的旋转平移
二维xy坐标系
如图是以 O O O为原点的 x y xy xy二维平面坐标系,平面上有一点 P ( x , y ) P(x, y) P(x,y),与原点 O O O的距离 O P = r OP=r OP=r,设 O P OP OP与坐标轴x的夹角为 α \alpha α; P ′ ( x ′ , y ′ ) P'(x',y') P′(x′,y′)是 P P P以 r r r为半径以 O O O为圆心逆时针旋转 β \beta β角度后得到的点

旋转
现在用 P P P以及来表示 P ′ P' P′
x ′ = r ∗ c o s ( α + β ) = r ∗ c o s α ∗ c o s β − r ∗ s i n α ∗ s i n β = x ∗ c o s β − y ∗ s i n β y ′ = r ∗ s i n ( α + β ) = r ∗ s i n α ∗ c o s β + r ∗ c o s α ∗ s i n β = x ∗ s i n β + y ∗ c o s β \begin{aligned} x'&=r*cos(\alpha+\beta)\\ &=r*cos\alpha * cos\beta-r*sin\alpha*sin\beta \\ &=x*cos\beta-y*sin\beta\\ y'&=r*sin(\alpha+\beta)\\ &=r*sin\alpha * cos\beta+r*cos\alpha*sin\beta \\ &=x*sin\beta+y*cos\beta \end{aligned} x′y′=r∗cos(α+β)=r∗cosα∗cosβ−r∗sinα∗sinβ=x∗cosβ−y∗sinβ=r∗sin(α+β)=r∗sinα∗cosβ+r∗cosα∗sinβ=x∗sinβ+y∗cosβ
用矩阵表示:
[ x ′ y ′ ] = [ c o s β − s i n β s i n β c o s β ] [ x y ] \begin{bmatrix} x' \\ y' \end{bmatrix}= \begin{bmatrix} cos\beta & -sin\beta \\ sin\beta & cos\beta \end{bmatrix}\begin{bmatrix} x \\ y \end{bmatrix} [x′y′]=[cosβsinβ−sinβcosβ][xy]
以上推广开来,二维平面上的点以坐标原点 O O O为中心,逆时针旋转了 β \beta β度。
图像坐标系
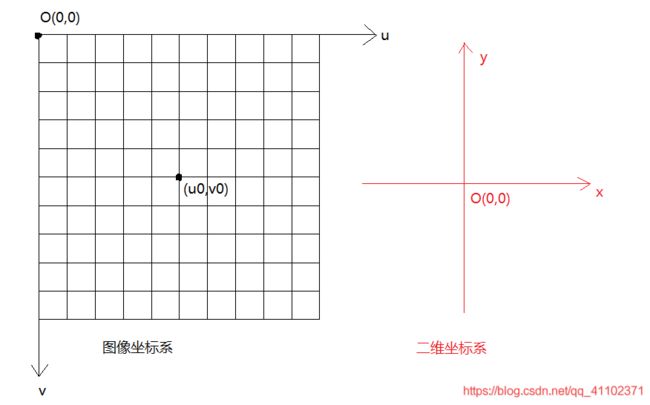
可以看到两坐标系的横轴 x x x与 u u u方向相同,纵轴 y y y与 v v v方向相反,上述的坐标公式表达是以二维xy坐标系的方向来思考的,那么在实际的图像坐标中:
旋转
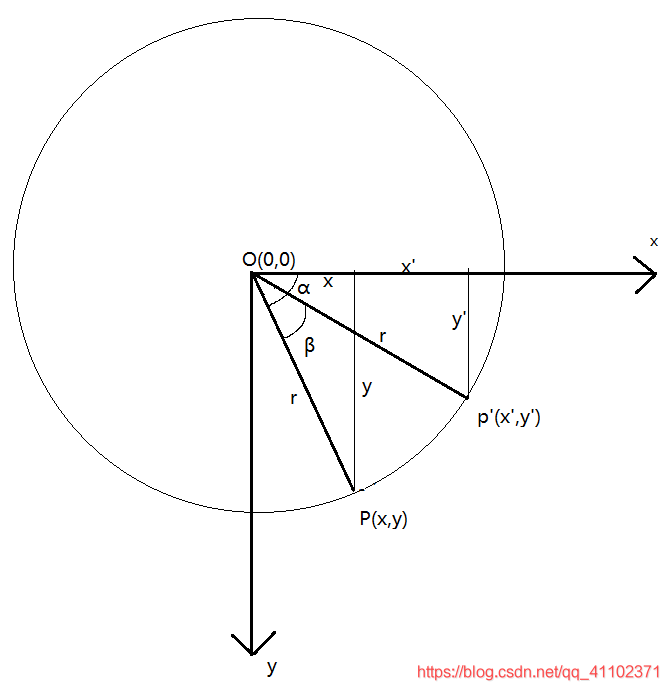
如图是以 O O O为原点的 u v uv uv图像平面坐标系,平面上有一点 P ( x , y ) P(x, y) P(x,y),与原点 O O O的距离 O P = r OP=r OP=r,设 O P OP OP与坐标轴x的夹角为 α \alpha α; P ′ ( x ′ , y ′ ) P'(x',y') P′(x′,y′)是 P P P以 r r r为半径以 O O O为圆心逆时针旋转 β \beta β角度后得到的点
x ′ = r ∗ c o s ( α − β ) = r ∗ c o s α ∗ c o s β + r ∗ s i n α ∗ s i n β = x ∗ c o s β + y ∗ s i n β y ′ = r ∗ s i n ( α − β ) = r ∗ s i n α ∗ c o s β − r ∗ c o s α ∗ s i n β = − x ∗ s i n β + y ∗ c o s β \begin{aligned} x'&=r*cos(\alpha-\beta)\\ &=r*cos\alpha * cos\beta+r*sin\alpha*sin\beta \\ &=x*cos\beta+y*sin\beta\\ y'&=r*sin(\alpha-\beta)\\ &=r*sin\alpha * cos\beta-r*cos\alpha*sin\beta \\ &=-x*sin\beta+y*cos\beta \end{aligned} x′y′=r∗cos(α−β)=r∗cosα∗cosβ+r∗sinα∗sinβ=x∗cosβ+y∗sinβ=r∗sin(α−β)=r∗sinα∗cosβ−r∗cosα∗sinβ=−x∗sinβ+y∗cosβ
用矩阵表示:
[ x ′ y ′ ] = [ c o s β s i n β − s i n β c o s β ] [ x y ] \begin{bmatrix} x' \\ y' \end{bmatrix}= \begin{bmatrix} cos\beta & sin\beta \\ -sin\beta & cos\beta \end{bmatrix}\begin{bmatrix} x \\ y \end{bmatrix} [x′y′]=[cosβ−sinβsinβcosβ][xy]
按照我们的常规思维,是希望图像绕着自己的中心旋转一个角度的,但是图像 ( u , v ) (u,v) (u,v)坐标系和笛卡尔坐标系是不一样的;下图是图像的像素坐标系,每个方格代表一个像素,图像的行数为 r o w s rows rows,列数为 c o l s cols cols;图像坐标原点 O O O在左上角,不同于图像中心 ( u 0 , v 0 ) = ( c o l s / 2 , r o w s / 2 ) (u_0,v_0)=(cols/2,rows/2) (u0,v0)=(cols/2,rows/2),因此要减去图像中心 ( u 0 , v 0 ) (u_0,v_0) (u0,v0)让图像中心移动到坐标原点上去,才能让图像绕着自己的图像中心旋转

因此
x ′ = ( x − u 0 ) ∗ c o s β + ( y − v 0 ) ∗ s i n β y ′ = − ( x − u 0 ) ∗ s i n β + ( y − v 0 ) ∗ c o s β \begin{aligned}x'&=(x-u_0)*cos\beta+(y-v0)*sin\beta\\ y'&=-(x-u_0)*sin\beta+(y-v0)*cos\beta \end{aligned} x′y′=(x−u0)∗cosβ+(y−v0)∗sinβ=−(x−u0)∗sinβ+(y−v0)∗cosβ
用矩阵表示:
[ x ′ y ′ ] = [ c o s β s i n β − s i n β c o s β ] [ x − u 0 y − v 0 ] \begin{bmatrix} x' \\ y' \end{bmatrix}= \begin{bmatrix} cos\beta & sin\beta \\ -sin\beta & cos\beta \end{bmatrix}\begin{bmatrix} x-u_0 \\ y-v_0 \end{bmatrix} [x′y′]=[cosβ−sinβsinβcosβ][x−u0y−v0]
但是旋转完成之后,我们得恢复图像中心,于是得加上之前减掉的 ( u 0 , v 0 ) (u_0,v_0) (u0,v0),
x ′ = ( x − u 0 ) ∗ c o s β + ( y − v 0 ) ∗ s i n β + u 0 = x ∗ c o s β + y ∗ s i n β + u 0 ( 1 − c o s β ) − v 0 s i n β y ′ = − ( x − u 0 ) ∗ s i n β + ( y − v 0 ) ∗ c o s β + v 0 = − x ∗ s i n β + y ∗ c o s β + u 0 s i n β + v 0 ( 1 − c o s β ) \begin{aligned} x' & = (x-u_0)*cos\beta+(y-v0)*sin\beta+u_0 \\ & = x*cos\beta+y*sin\beta+u_0(1-cos\beta)-v_0sin\beta\\ y' &=-(x-u_0)*sin\beta+(y-v0)*cos\beta+v_0\\ &=-x*sin\beta+y*cos\beta+u_0sin\beta+v_0(1-cos\beta) \end{aligned} x′y′=(x−u0)∗cosβ+(y−v0)∗sinβ+u0=x∗cosβ+y∗sinβ+u0(1−cosβ)−v0sinβ=−(x−u0)∗sinβ+(y−v0)∗cosβ+v0=−x∗sinβ+y∗cosβ+u0sinβ+v0(1−cosβ)
齐次坐标矩阵表示:
[ x ′ y ′ 1 ] = [ c o s β s i n β u 0 ( 1 − c o s β ) − v 0 s i n β − s i n β c o s β v 0 ( 1 − c o s β ) + u 0 s i n β 0 0 1 ] [ x y 1 ] \begin{bmatrix} x' \\ y'\\1 \end{bmatrix}= \begin{bmatrix} cos\beta & sin\beta & u_0(1-cos\beta)-v_0sin\beta \\ -sin\beta & cos\beta &v_0(1-cos\beta)+u_0sin\beta\\ 0&0&1 \end{bmatrix}\begin{bmatrix} x \\ y\\1 \end{bmatrix} ⎣⎡x′y′1⎦⎤=⎣⎡cosβ−sinβ0sinβcosβ0u0(1−cosβ)−v0sinβv0(1−cosβ)+u0sinβ1⎦⎤⎣⎡xy1⎦⎤
旋转平移
我们可以再加上 ( u 1 , v 1 ) (u_1,v_1) (u1,v1)达到图像平移的效果
x ′ = ( x − u 0 ) ∗ c o s β + ( y − v 0 ) ∗ s i n β + u 0 + u 1 = x ∗ c o s β + y ∗ s i n β + u 0 ( 1 − c o s β ) − v 0 s i n β + u 1 y ′ = − ( x − u 0 ) ∗ s i n β + ( y − v 0 ) ∗ c o s β + v 0 + v 1 = − x ∗ s i n β + y ∗ c o s β + u 0 s i n β + v 0 ( 1 − c o s β ) + v 1 \begin{aligned} x' & = (x-u_0)*cos\beta+(y-v0)*sin\beta+u_0 +u_1\\ & = x*cos\beta+y*sin\beta+u_0(1-cos\beta)-v_0sin\beta+u_1\\ y' &=-(x-u_0)*sin\beta+(y-v0)*cos\beta+v_0+v_1\\ &=-x*sin\beta+y*cos\beta+u_0sin\beta+v_0(1-cos\beta)+v_1 \end{aligned} x′y′=(x−u0)∗cosβ+(y−v0)∗sinβ+u0+u1=x∗cosβ+y∗sinβ+u0(1−cosβ)−v0sinβ+u1=−(x−u0)∗sinβ+(y−v0)∗cosβ+v0+v1=−x∗sinβ+y∗cosβ+u0sinβ+v0(1−cosβ)+v1
矩阵表示:
[ x ′ y ′ 1 ] = [ c o s β s i n β u 0 ( 1 − c o s β ) − v 0 s i n β + u 1 − s i n β c o s β v 0 ( 1 − c o s β ) + u 0 s i n β + v 1 0 0 1 ] [ x y 1 ] \begin{bmatrix} x' \\ y'\\1 \end{bmatrix}= \begin{bmatrix} cos\beta & sin\beta & u_0(1-cos\beta)-v_0sin\beta+u_1 \\ -sin\beta & cos\beta &v_0(1-cos\beta)+u_0sin\beta+v_1\\ 0&0&1 \end{bmatrix}\begin{bmatrix} x \\ y\\1 \end{bmatrix} ⎣⎡x′y′1⎦⎤=⎣⎡cosβ−sinβ0sinβcosβ0u0(1−cosβ)−v0sinβ+u1v0(1−cosβ)+u0sinβ+v11⎦⎤⎣⎡xy1⎦⎤
旋转平移缩放
我们还可以在矩阵中乘以一个缩放系数 s s s对坐标进行缩放,达到图像缩放的目的
[ x ′ y ′ 1 ] = [ c o s β ∗ s s i n β ∗ s u 0 ( 1 − c o s β ) − v 0 s i n β + u 1 − s i n β ∗ s c o s β ∗ s v 0 ( 1 − c o s β ) + u 0 s i n β + v 1 0 0 1 ] [ x y 1 ] \begin{bmatrix} x' \\ y'\\1 \end{bmatrix}= \begin{bmatrix} cos\beta*s & sin\beta *s & u_0(1-cos\beta)-v_0sin\beta+u_1 \\ -sin\beta *s & cos\beta *s &v_0(1-cos\beta)+u_0sin\beta+v_1\\ 0&0&1 \end{bmatrix}\begin{bmatrix} x \\ y\\1 \end{bmatrix} ⎣⎡x′y′1⎦⎤=⎣⎡cosβ∗s−sinβ∗s0sinβ∗scosβ∗s0u0(1−cosβ)−v0sinβ+u1v0(1−cosβ)+u0sinβ+v11⎦⎤⎣⎡xy1⎦⎤
特殊情况
当旋转角度 β = 0 \beta=0 β=0,平移量 ( u 1 , v 1 ) = ( 0 , 0 ) (u_1,v_1)=(0,0) (u1,v1)=(0,0),缩放系数 s = 1 s=1 s=1时,相当于没有对图像做变换,将上述参数带入矩阵可得
[ x ′ y ′ 1 ] = [ 1 0 0 0 1 0 0 0 1 ] [ x y 1 ] \begin{bmatrix} x' \\ y'\\1 \end{bmatrix}= \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 &0\\ 0&0&1 \end{bmatrix}\begin{bmatrix} x \\ y\\1 \end{bmatrix} ⎣⎡x′y′1⎦⎤=⎣⎡100010001⎦⎤⎣⎡xy1⎦⎤
可得:
x ′ = x y ′ = y x'=x\\ y'=y x′=xy′=y
与实际一致
2、单应性变换
单应性主要针对的是图像中我们关心的目标区域处于同一平面,或者说目标处的起伏与相机到目标之间的距离比起来非常小,可以近似看成平面;在三维重建structure from motion中,如果两幅图像之间的60%的特征点都满足单应性,是不宜作为初始像对的,因为此时的特征点大多处于同一平面,对sfm来说是不好的;关于单应性变换的理解,可以阅读这篇文章,讲得很好:单应性Homograph估计:从传统算法到深度学习 https://zhuanlan.zhihu.com/p/74597564
仿射变换
对于上面的旋转平移缩放矩阵,如果 x , y x,y x,y加以不同的缩放因子,比如 x , y x,y x,y轴的缩放因子分别是 s 1 , s 2 s_1,s_2 s1,s2
[ x ′ y ′ 1 ] = [ c o s β ∗ s 1 s i n β ∗ s 2 u 0 ( 1 − c o s β ) − v 0 s i n β + u 1 − s i n β ∗ s 2 c o s β ∗ s 1 v 0 ( 1 − c o s β ) + u 0 s i n β + v 1 0 0 1 ] [ x y 1 ] \begin{bmatrix} x' \\ y'\\1 \end{bmatrix}= \begin{bmatrix} cos\beta*s1 & sin\beta *s2 & u_0(1-cos\beta)-v_0sin\beta+u_1 \\ -sin\beta *s2 & cos\beta *s1 &v_0(1-cos\beta)+u_0sin\beta+v_1\\ 0&0&1 \end{bmatrix}\begin{bmatrix} x \\ y\\1 \end{bmatrix} ⎣⎡x′y′1⎦⎤=⎣⎡cosβ∗s1−sinβ∗s20sinβ∗s2cosβ∗s10u0(1−cosβ)−v0sinβ+u1v0(1−cosβ)+u0sinβ+v11⎦⎤⎣⎡xy1⎦⎤
其中
H = [ h 11 h 12 h 13 h 21 h 22 h 23 h 31 h 32 h 33 ] = [ c o s β ∗ s 1 s i n β ∗ s 2 u 0 ( 1 − c o s β ) − v 0 s i n β + u 1 − s i n β ∗ s 2 c o s β ∗ s 1 v 0 ( 1 − c o s β ) + u 0 s i n β + v 1 0 0 1 ] H=\begin{bmatrix} h_{11} & h_{12} & h_{13}\\ h_{21} & h_{22} & h_{23}\\ h_{31} & h_{32} & h_{33} \end{bmatrix}= \begin{bmatrix} cos\beta*s1 & sin\beta *s2 & u_0(1-cos\beta)-v_0sin\beta+u_1 \\ -sin\beta *s2 & cos\beta *s1 &v_0(1-cos\beta)+u_0sin\beta+v_1\\ 0&0&1 \end{bmatrix} H=⎣⎡h11h21h31h12h22h32h13h23h33⎦⎤=⎣⎡cosβ∗s1−sinβ∗s20sinβ∗s2cosβ∗s10u0(1−cosβ)−v0sinβ+u1v0(1−cosβ)+u0sinβ+v11⎦⎤
H H H就是一个仿射变换矩阵
透视变换
当上述 H H H矩阵的 h 31 , h 32 h_{31},h_{32} h31,h32不为0时, H H H是个透视变换矩阵
H = [ c o s β ∗ s 1 s i n β ∗ s 2 u 0 ( 1 − c o s β ) − v 0 s i n β + u 1 − s i n β ∗ s 2 c o s β ∗ s 1 v 0 ( 1 − c o s β ) + u 0 s i n β + v 1 k 1 k 2 1 ] H= \begin{bmatrix} cos\beta*s1 & sin\beta *s2 & u_0(1-cos\beta)-v_0sin\beta+u_1 \\ -sin\beta *s2 & cos\beta *s1 &v_0(1-cos\beta)+u_0sin\beta+v_1\\ k_1&k_2&1 \end{bmatrix} H=⎣⎡cosβ∗s1−sinβ∗s2k1sinβ∗s2cosβ∗s1k2u0(1−cosβ)−v0sinβ+u1v0(1−cosβ)+u0sinβ+v11⎦⎤
3、opencv实验
首先看一段代码:
\opencv-4.4.0\modules\imgproc\src\imgwarp.cpp
cv::Matx23d cv::getRotationMatrix2D_(Point2f center, double angle, double scale)
{
CV_INSTRUMENT_REGION();
angle *= CV_PI/180;
double alpha = std::cos(angle)*scale;
double beta = std::sin(angle)*scale;
Matx23d M(
alpha, beta, (1-alpha)*center.x - beta*center.y,
-beta, alpha, beta*center.x + (1-alpha)*center.y
);
return M;
}
这是opencv提供的获取旋转矩阵的函数,输入是旋转中心、角度、缩放系数,输出是一个2x3的变换矩阵,对比上面的推导
[ x ′ y ′ 1 ] = [ c o s β ∗ s s i n β ∗ s u 0 ( 1 − c o s β ) − v 0 s i n β + u 1 − s i n β ∗ s c o s β ∗ s v 0 ( 1 − c o s β ) + u 0 s i n β + v 1 0 0 1 ] [ x y 1 ] \begin{bmatrix} x' \\ y'\\1 \end{bmatrix}= \begin{bmatrix} cos\beta*s & sin\beta *s & u_0(1-cos\beta)-v_0sin\beta+u_1 \\ -sin\beta *s & cos\beta *s &v_0(1-cos\beta)+u_0sin\beta+v_1\\ 0&0&1 \end{bmatrix}\begin{bmatrix} x \\ y\\1 \end{bmatrix} ⎣⎡x′y′1⎦⎤=⎣⎡cosβ∗s−sinβ∗s0sinβ∗scosβ∗s0u0(1−cosβ)−v0sinβ+u1v0(1−cosβ)+u0sinβ+v11⎦⎤⎣⎡xy1⎦⎤
[ x ′ y ′ ] = [ c o s β ∗ s s i n β ∗ s u 0 ( 1 − c o s β ) − v 0 s i n β + u 1 − s i n β ∗ s c o s β ∗ s v 0 ( 1 − c o s β ) + u 0 s i n β + v 1 ] [ x y 1 ] \begin{bmatrix} x' \\ y' \end{bmatrix}= \begin{bmatrix} cos\beta*s & sin\beta *s & u_0(1-cos\beta)-v_0sin\beta+u_1 \\ -sin\beta *s & cos\beta *s &v_0(1-cos\beta)+u_0sin\beta+v_1 \end{bmatrix}\begin{bmatrix} x \\ y\\1 \end{bmatrix} [x′y′]=[cosβ∗s−sinβ∗ssinβ∗scosβ∗su0(1−cosβ)−v0sinβ+u1v0(1−cosβ)+u0sinβ+v1]⎣⎡xy1⎦⎤
观察代码中的M矩阵,除了没有加上平移量 ( u 1 , v ! ) (u_1,v_!) (u1,v!),其余部分是完全对应的,此函数就是通过传入旋转中心、旋转角度、缩放系数3个参数来计算出一个旋转、缩放的变换矩阵;可能有人问那平移怎么实现呢,使用这个函数确实不能实现,下文会讲到可以在获取M矩阵后对其进行进一步的更改。
图像的旋转平移缩放实现
代码
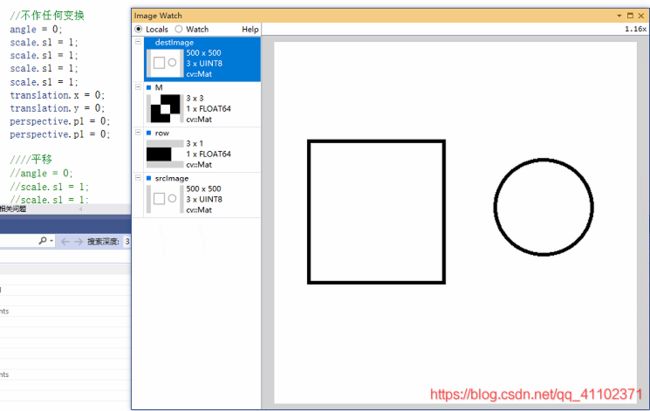
#include 下面实验结果,实验使用的原图(500x500)如下,调试时查看mat的工具为image watch:opencv用VS2013调试时用Image Watch插件查看图片 https://blog.csdn.net/mao_hui_fei/article/details/80951075
不作任何变换
平移
变换矩阵, h 13 h_{13} h13与 h 23 h_{23} h23是平移量

变换结果

平移+旋转
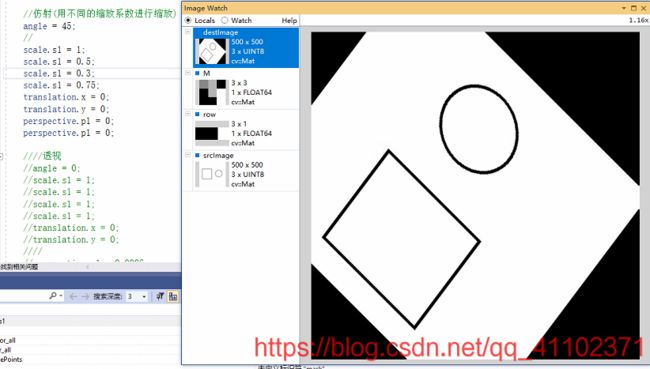
仿射(用不同的缩放系数进行缩放)
透视
坐标系变换与图像坐标变换
图像的旋转平移是在同一坐标系下的坐标变换,为什么要加上同一坐标系下,因为得和坐标系变换作出区别
上述对图像的一系列操作,可以这样想象:
将摄像头固定,将图像打印至A4纸,把图像在空间中使用不同姿态、不同距离放置,每次拍照,便可得到上述变换的结果。比如上述的透视,像不像正对你的图像被侧放了一个角度时的视觉效果。
而坐标系变换,可以这样类比:
将打印的图像或目标物体放在固定的地方,用摄像机从不同距离、不同角度去拍摄目标,于是在多幅图像之间就涉及到了空间坐标系的变换以及多视图几何。
这两种变换在进行公式推时候是有细微差别的,后面有空的话再写一篇空间坐标系变换的文章联系起来。
完
相比于出去人挤人汗流浃背,个人还是觉得躺家里睡觉舒服,不过今天白天着实睡太多了,不妥不妥。
各位劳动节快乐!
如有错漏,敬请指正
--------------------------------------------------------------------------------------------诺有缸的高飞鸟202105