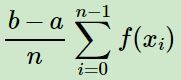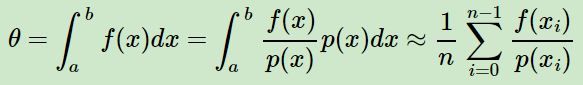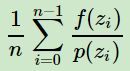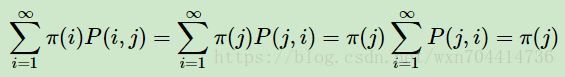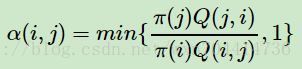蒙特卡罗 马尔科夫链 与Gibbs采样

        这几个概念看了挺多遍都还是含混不清，最近看了几篇博客，才算大致理解了一点点皮毛，所以来总结一下。

MCMC概述

        从名字我们可以看出，MCMC由两个MC组成，即蒙特卡罗方法（Monte Carlo Simulation，简称MC）和马尔科夫链（Markov Chain ，也简称MC）。要弄懂MCMC的原理我们首先得搞清楚蒙特卡罗方法和马尔科夫链的原理

MCMC(一)蒙特卡罗方法（详见https://www.cnblogs.com/pinard/p/6625739.html）

       蒙特卡罗方法是一种随机模拟的方法，最早的蒙特卡罗方法是用来求积分的。通常我们可以用下面的方法求积分

但这个公式是假定x在[a, b]之间均匀分布的，而实际情况中绝大部分都是非均匀分布的，所以如果我们可以得到x的概率分布函数p(x)，那么就可以用下面的式子求积分

所以如果求出了x的概率分布，我们可以基于概率分布去采样基于这个概率分布的n个x的样本集，带入蒙特卡罗求和的式子即可求解。那么我们现在的问题转到了如何求出x的分布p(x)对应的若干个样本f(xi)。

       对于常见的均匀分布uniform(0,1)是非常容易采样样本的，一般通过线性同余发生器可以很方便的生成(0,1)之间的伪随机数样本。而其他常见的概率分布，无论是离散的分布还是连续的分布，它们的样本都可以通过uniform(0,1)的样本转换而得。

       不过很多时候，我们的x的概率分布不是常见的分布，这意味着我们没法方便的得到这些非常见的概率分布的样本集。对于概率分布不是常见的分布，一个可行的办法是采用接受-拒绝采样来得到该分布的样本。既然 p(x) 太复杂在程序中没法直接采样，那么我设定一个程序可采样的分布 q(x) 比如高斯分布，然后按照一定的方法拒绝某些样本，以达到接近 p(x) 分布的目的，其中q(x)叫做 proposal distribution。

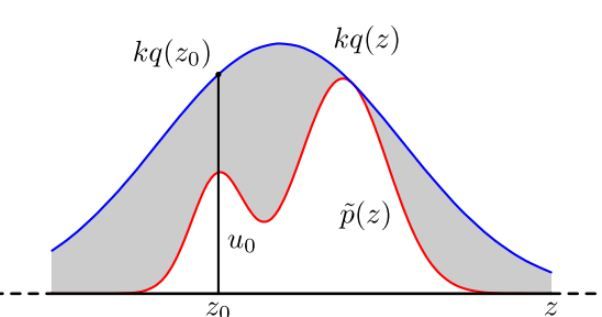
具体采用过程如下，设定一个方便采样的常用概率分布函数 q(x)，以及一个常量 k，使得 p(x) 总在 kq(x) 的下方。如上图。

　　首先，采样得到q(x)的一个样本z0，采样方法如第三节。然后，从均匀分布（0,kq(z0))中采样得到一个值u。如果u落在了上图中的灰色区域，则拒绝这次抽样，否则接受这个样本z0。重复以上过程得到n个接受的样本z0,z1,...zn−1,则最后的蒙特卡罗方法求解结果为：

整个过程中，我们通过一系列的接受拒绝决策来达到用q(x)模拟p(x)概率分布的目的。

蒙特卡罗方法小结

       使用接受-拒绝采样，我们可以解决一些概率分布不是常见的分布的时候，得到其采样集并用蒙特卡罗方法求和的目的。但是接受-拒绝采样也只能部分满足我们的需求，在很多时候我们还是很难得到我们的概率分布的样本集。比如：

　　1）对于一些二维分布p(x,y)，有时候我们只能得到条件分布p(x|y)和p(y|x)和,却很难得到二维分布p(x,y)一般形式，这时我们无法用接受-拒绝采样得到其样本集。

　　2）对于一些高维的复杂非常见分布p(x1,x2,...,xn)，我们要找到一个合适的q(x)和k非常困难。

　　从上面可以看出，要想将蒙特卡罗方法作为一个通用的采样模拟求和的方法，必须解决如何方便得到各种复杂概率分布对应的采样样本集的问题。而马尔科夫链正好可以帮助我们找到这些复杂概率分布对应的采样样本集。

MCMC(二)马尔科夫链（详见https://www.cnblogs.com/pinard/p/6632399.html）

       马尔科夫链定义本身比较简单，它假设某一时刻状态转移的概率只依赖于它的前一个状态。如果用精确的数学定义来描述，则假设我们的序列状态是...Xt−2,Xt−1,Xt,Xt+1,...，那么我们的在时刻Xt+1的状态的条件概率仅仅依赖于时刻Xt，即：

既然某一时刻状态转移的概率只依赖于它的前一个状态，那么我们只要能求出系统中任意两个状态之间的转换概率，这个马尔科夫链的模型就定了。

那么马尔科夫链模型的状态转移矩阵和我们蒙特卡罗方法需要的概率分布样本集有什么关系呢？这需要从马尔科夫链模型的状态转移矩阵的性质讲起。

马尔科夫链模型状态转移矩阵的性质

       马尔科夫链模型的状态转移矩阵收敛到的稳定概率分布与我们的初始状态概率分布无关。这是一个非常好的性质，也就是说，如果我们得到了这个稳定概率分布对应的马尔科夫链模型的状态转移矩阵，则我们可以用任意的概率分布样本开始，带入马尔科夫链模型的状态转移矩阵，这样经过一些序列的转换，最终就可以得到符合对应稳定概率分布的样本。

       同时，对于一个确定的状态转移矩阵P，它的n次幂Pn在当n大于一定的值的时候也可以发现是确定的。

       用数学语言总结下马尔科夫链的收敛性质如下。

π 通常称为马尔科夫链的平稳分布。

所以基于马尔科夫链采样如下。

1）输入马尔科夫链状态转移矩阵P，设定状态转移次数阈值n1，需要的样本个数n2
2）从任意简单概率分布采样得到初始状态值x0
3）for t=0 to n1+n2−1: 从条件概率分布P(x|xt)中采样得到样本xt+1

样本集(xn1,xn1+1,...,xn1+n2−1)即为我们需要的平稳分布对应的样本集。

       所以，如果假定我们可以得到我们需要采样样本的平稳分布所对应的马尔科夫链状态转移矩阵，那么我们就可以用马尔科夫链采样得到我们需要的样本集，进而进行蒙特卡罗模拟。但是一个重要的问题是，随意给定一个平稳分布π，如何得到它所对应的马尔科夫链状态转移矩阵P呢？MCMC采样通过迂回的方式解决了这个问题。

MCMC(三)MCMC采样和M-H采样（详见https://www.cnblogs.com/pinard/p/6638955.html）

       在解决从平稳分布π, 找到对应的马尔科夫链状态转移矩阵P之前，我们还需要先看看马尔科夫链的细致平稳条件。定义如下。如果非周期马尔科夫链的状态转移矩阵P和概率分布π(x)对于所有的i,j满足：π(i)P(i,j)=π(j)P(j,i)，则称概率分布π(x)是状态转移矩阵P的平稳分布。证明很简单，即

将上式用矩阵表示即为：πP=π

       可以发现马尔科夫链的细致平稳条件满足马尔可夫链的收敛性质。也就是说，只要我们找到了可以使概率分布π(x)满足细致平稳分布的矩阵P即可。这给了我们寻找从平稳分布π, 找到对应的马尔科夫链状态转移矩阵P的新思路。但不幸的是，我们的目标平稳分布是π(x)，随机找一个马尔科夫链状态转移矩阵Q，它是很难满足细致平稳条件的。即π(i)Q(i,j)≠π(j)Q(j,i)。

MCMC采样

       由于一般情况下，目标平稳分布π(x)和某一个马尔科夫链状态转移矩阵Q不满足细致平稳条件，我们可以对公式π(i)P(i,j)=π(j)P(j,i)做一个改造，使细致平稳条件成立。方法是引入一个α(i,j),使上式可以取等号，即：

α(i,j)满足α(i,j)=π(j)Q(j,i)  α(j,i)=π(i)Q(i,j)

我们就得到了我们的分布π(x)对应的马尔科夫链状态转移矩阵P，满足：

也就是说，我们的目标矩阵P可以通过任意一个马尔科夫链状态转移矩阵Q乘以α(i,j)得到。α(i,j)我们有一般称之为接受率。取值在[0,1]之间，可以理解为一个概率值。即目标矩阵P可以通过任意一个马尔科夫链状态转移矩阵Q以一定的接受率获得。

MCMC的采样过程如下：
　　1）输入我们任意选定的马尔科夫链状态转移矩阵Q，平稳分布π(x)，设定状态转移次数阈值n1，需要的样本个数n2
　　2）从任意简单概率分布采样得到初始状态值x0
　　3）for t=0 to n1+n2−1: 
　　　　a) 从条件概率分布Q(x|xt)中采样得到样本x∗
　　　　b) 从均匀分布采样u∼uniform[0,1]
　　　　c) 如果u<α(xt,x∗)=π(x∗)Q(x∗,xt), 则接受转移xt→x∗，即xt+1=x∗
　　　　d) 否则不接受转移，t=max(t−1,0)
　　样本集(xn1,xn1+1,...,xn1+n2−1)即为我们需要的平稳分布对应的样本集。

       上面这个过程基本上就是MCMC采样的完整采样理论了，但是这个采样算法还是比较难在实际中应用，问题在上面第三步的c步骤，接受率这儿。由于α(xt,x∗)可能非常的小，比如0.1，导致我们大部分的采样值都被拒绝转移，采样效率很低。有可能我们采样了上百万次马尔可夫链还没有收敛，也就是上面这个n1要非常非常的大，这让人难以接受。这时M-H采样出场了。

M-H采样

       M-H采样是Metropolis-Hastings采样的简称，这个算法首先由Metropolis提出，被Hastings改进，因此被称之为Metropolis-Hastings采样或M-H采样。M-H采样解决了我们上一节MCMC采样接受率过低的问题。

将接受率可以做如下改进，即：

通过这个微小的改造，我们就得到了可以在实际应用中使用的M-H采样算法过程如下：
　　1）输入我们任意选定的马尔科夫链状态转移矩阵Q，平稳分布π(x)，设定状态转移次数阈值n1，需要的样本个数n2
　　2）从任意简单概率分布采样得到初始状态值x0
　　3）for t=0 to n1+n2−1: 
　　　　a) 从条件概率分布Q(x|xt)中采样得到样本x∗
　　　　b) 从均匀分布采样u∼uniform[0,1]
　　　　c) 如果u<α(xt,x∗)=min{ π(j)Q(j,i) / π(i)Q(i,j), 1}, 则接受转移xt→x∗，即xt+1=x∗
　　　　d) 否则不接受转移，t=max(t−1,0)
　　样本集(xn1,xn1+1,...,xn1+n2−1)即为我们需要的平稳分布对应的样本集。
       很多时候，我们选择的马尔科夫链状态转移矩阵Q如果是对称的，即满足Q(i,j)=Q(j,i),这时我们的接受率可以进一步简化为：

α(i,j)=min{ π(j) / π(i), 1}

M-H采样总结

       M-H采样完整解决了使用蒙特卡罗方法需要的任意概率分布样本集的问题，因此在实际生产环境得到了广泛的应用。但是在大数据时代，M-H采样面临着两大难题：
      1） 我们的数据特征非常的多，M-H采样由于接受率计算式π(j)Q(j,i)/π(i)Q(i,j)的存在，在高维时需要的计算时间非常的可观，算法效率很低。同时α(i,j)一般小于1，有时候辛苦计算出来却被拒绝了。能不能做到不拒绝转移呢？
       2） 由于特征维度大，很多时候我们甚至很难求出目标的各特征维度联合分布，但是可以方便求出各个特征之间的条件概率分布。这时候我们能不能只有各维度之间条件概率分布的情况下方便的采样呢？
Gibbs采样解决了上面两个问题，因此在大数据时代，MCMC采样基本是Gibbs采样的天下。

MCMC(四)Gibbs采样（详见https://www.cnblogs.com/pinard/p/6645766.html）

重新寻找合适的细致平稳条件

二维Gibbs采样
　　利用上一节找到的状态转移矩阵，我们就得到了二维Gibbs采样，这个采样需要两个维度之间的条件概率。具体过程如下：
　　1）输入平稳分布π(x1,x2)，设定状态转移次数阈值n1，需要的样本个数n2
　　2）随机初始化初始状态值x1(0)和x2(0)
　　3）for t=0 to n1+n2−1: 
　　　　　a) 从条件概率分布P(x2|x1(t))中采样得到样本x2(t+1)
　　　　　b) 从条件概率分布P(x1|x2(t+1))中采样得到样本x1(t+1)

　   样本集即为我们需要的平稳分布对应的样本集。

　　整个采样过程中，我们通过轮换坐标轴，采样的过程为：

　　当然，坐标轴轮换不是必须的，我们也可以每次随机选择一个坐标轴进行采样。不过常用的Gibbs采样的实现都是基于坐标轴轮换的。

多维Gibbs采样

　　上面的这个算法推广到多维的时候也是成立的。比如一个n维的概率分布π(x1,x2,...xn)，我们可以通过在n个坐标轴上轮换采样，来得到新的样本。对于轮换到的任意一个坐标轴xi上的转移，马尔科夫链的状态转移概率为P(xi|x1,x2,...,xi−1,xi+1,...,xn)，即固定n−1个坐标轴，在某一个坐标轴上移动。

　　具体的算法过程如下：

　　　　1）输入平稳分布π(x1,x2，...,xn)或者对应的所有特征的条件概率分布，设定状态转移次数阈值n1，需要的样本个数n2
　　　　2）随机初始化初始状态值(x(0)1,x(0)2,...,x(0)n
　　　　3）for t=0 to n1+n2−1: 
　　　　　　a) 从条件概率分布P(x1|x2(t),x3(t),...,xn(t))中采样得到样本x1(t+1)
　　　　　　b) 从条件概率分布P(x2|x1(t+1),x3(t),x4(t),...,xn(t))中采样得到样本x2(t+1)
　　　　　　c)...
　　　　　　d) 从条件概率分布P(xj|x1(t+1),x2(t+1),...,xj−1(t+1),xj+1(t)...,xn(t))中采样得到样本xj(t+1)
　　　　　　e)...
　　　　　　f) 从条件概率分布P(xn|x1(t+1),x2(t+1),...,xn-1(t+1))中采样得到样本xn(t+1)

　　　　样本集{(x1(n1),x2(n1),...,xn(n1)),...,(x1(n1+n2−1),x2(n1+n2−1),...,xn(n1+n2−1))}即为我们需要的平稳分布对应的样本集。

　　整个采样过程和Lasso回归的坐标轴下降法算法非常类似，只不过Lasso回归是固定n−1个特征，对某一个特征求极值。而Gibbs采样是固定n−1个特征在某一个特征采样。同样的，轮换坐标轴不是必须的，我们可以随机选择某一个坐标轴进行状态转移，只不过常用的Gibbs采样的实现都是基于坐标轴轮换的。

       至此，Gibbs采样方法在没有接受概率与特征维度联合分布的情况下同样完成了对任意概率分布样本集的采样问题。

       以下是自己结合全篇内容对MCMC，马尔科夫链，Gibbs采样这几个问题之间关系的理解。                                             总结文章的整个思路就是要用蒙特卡罗方法求和，就得解决任意概率分布样本集的采样问题，而由马尔科夫链的性质可知，如果得到平稳分布对应的状态转移矩阵P，那么从任意初始状态开始就可以用马尔科夫链采样得到我们需要的样本集。问题在于随意给定一个平稳分布π，如何得到它所对应的马尔科夫链状态转移矩阵P呢？这就是MCMC解决的问题。由于马尔科夫的细致平稳条件（如果非周期马尔科夫链的状态转移矩阵P和概率分布π(x)对于所有的i,j满足：π(i)P(i,j)=π(j)P(j,i)，则称概率分布π(x)是状态转移矩阵P的平稳分布。）同样满足马尔科夫链的收敛条件（πP=π），所以只要找到使π(x)满足细致平稳条件的P，也就是找到了状态转移矩阵P。由于对一个π(x)很难随机找到一个马尔科夫状态转移矩阵Q满足细致平稳分布，所以通过改进，引入接受率α(i,j)，可以得到P(i,j)=Q(i,j)α(i,j)，所以我们的目标矩阵P可以通过任意一个马尔科夫链状态转移矩阵Q乘以α(i,j)得到。但同时由于α(i,j)太小，所以M-H方法做了改进。最后由于大数据背景下，在高维情况下，由于接受率的原因导致算法收敛时间变长，再一个特征的条件概率好计算然而联合分布概率却不好计算，所以Gibbs采样出现了。Gibbs采样避开使用接受率与联合分布概率，直接采用条件分布概率来得到任意概率分布下的样本，进而解决了任意概率分布下的样本采集问题。