PHP实现排序算法----归并排序（Merging Sort）

基本思想：

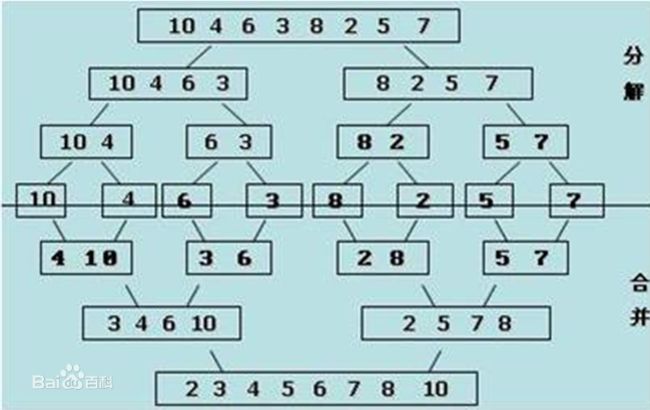
归并排序：就是利用归并（合并）的思想实现的排序方法。它的原理是假设初始序列含有 n 个元素，则可以看成是 n 个有序的子序列，每个子序列的长度为 1，然后两两归并，得到 ⌈ n / 2⌉ （⌈ x ⌉ 表示不小于 x 的最小整数）个长度为 2 或 1 的有序序列；再两两归并，······，如此重复，直至得到一个长度为 n 的有序序列为止，这种排序方法就成为 2 路归并排序。

一、归并的过程：

a[i] 取 a 数组的前部分（已经排好序），a[j] 取 a 数组的后部分（已经排好序）
r 数组存储排好序的 a 数组

比较 a[i]和 a[j] 的大小，若 a[i] ≤ a[j]，则将第一个有序表中的元素 a[i] 复制到 r[k] 中，并令 i 和 k 分别加上 1；否则将第二个有序表中的元素 a[j] 复制到 r[k] 中，并令 j 和 k 分别加上 1，如此循环下去，直到其中一个有序表取完，然后再将另一个有序表中剩余的元素复制到 r 中从下标 k 到下标 t 的单元。归并排序的算法我们通常用递归实现，先把待排序区间 [s,t] 以中点二分，接着把左边子区间排序，再把右边子区间排序，最后把左区间和右区间用一次归并操作合并成有序的区间 [s,t]。

二、归并操作：

归并操作(merge)，也叫归并算法，指的是将两个顺序序列合并成一个顺序序列的方法。

如　设有数列{6，202，100，301，38，8，1}

初始状态：6 , 202 , 100 , 301 , 38 , 8，1

第一次归并后：{6,202},{100,301},{8,38},{1}，比较次数：3；

第二次归并后：{6,100,202,301}，{1,8,38}，比较次数：4；

第三次归并后：{1,6,8,38,100,202,301},比较次数：4；

总的比较次数为：3+4+4=11,；

逆序数为14；

三、算法描述：

归并操作的工作原理如下：

第一步：申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列

第二步：设定两个指针，最初位置分别为两个已经排序序列的起始位置

第三步：比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置

重复步骤3直到某一指针超出序列尾

将另一序列剩下的所有元素直接复制到合并序列尾

算法实现：

我们先来看看主函数部分：

//交换函数
function swap(array &$arr,$a,$b){
     
    $temp = $arr[$a];
    $arr[$a] = $arr[$b];
    $arr[$b] = $temp;
}

//归并算法总函数
function MergeSort(array &$arr){
     
    $start = 0;
    $end = count($arr) - 1;
    MSort($arr,$start,$end);
}

在总函数中，我们只调用了一个 MSort() 函数，因为我们要使用递归调用，所以将 MSort() 封装起来。

下面我们来看看 MSort() 函数：

function MSort(array &$arr,$start,$end){
    //当子序列长度为1时，$start == $end，不用再分组
    if($start < $end){
        $mid = floor(($start + $end) / 2);	//将 $arr 平分为 $arr[$start - $mid] 和 $arr[$mid+1 - $end]
        MSort($arr,$start,$mid);			//将 $arr[$start - $mid] 归并为有序的$arr[$start - $mid]
        MSort($arr,$mid + 1,$end);			//将 $arr[$mid+1 - $end] 归并为有序的 $arr[$mid+1 - $end]
        Merge($arr,$start,$mid,$end);       //将$arr[$start - $mid]部分和$arr[$mid+1 - $end]部分合并起来成为有序的$arr[$start - $end]
    }
}

上面的 MSort() 函数实现将数组分半再分半（直到子序列长度为1），然后将子序列合并起来。

现在是我们的归并操作函数 Merge() :

//归并操作
function Merge(array &$arr,$start,$mid,$end){
     
    $i = $start;
    $j=$mid + 1;
    $k = $start;
    $temparr = array();

    while($i!=$mid+1 && $j!=$end+1)
    {
       if($arr[$i] >= $arr[$j]){
           $temparr[$k++] = $arr[$j++];
       }
       else{
           $temparr[$k++] = $arr[$i++];
       }
    }

    //将第一个子序列的剩余部分添加到已经排好序的 $temparr 数组中
    while($i != $mid+1){
        $temparr[$k++] = $arr[$i++];
    }
    //将第二个子序列的剩余部分添加到已经排好序的 $temparr 数组中
    while($j != $end+1){
        $temparr[$k++] = $arr[$j++];
    }
    for($i=$start; $i<=$end; $i++){
        $arr[$i] = $temparr[$i];
    }
}

到了这里，我们的归并算法就完了。我们调用试试：

$arr = array(9,1,5,8,3,7,4,6,2);
MergeSort($arr);
var_dump($arr);

复杂度分析：

由于归并算法无论原来的序列是否有序都会进行分组和比较，因此它的最好、最坏、平均的时间复杂度都是 O(nlogn)。

归并算法是一种稳定的排序算法。

本篇博客参考自《大话数据结构》。