欣小白的点滴 ————协同过滤算法
一.推荐系统的简述。
Resnick和Varian于1997年给出了被大家广泛接受的关于推荐系统的描述:“它利用电子商务网站向客户提供了商品的信息和建议,帮助用户决定购买产品的选择,以及模拟销售人员帮助用户完成购买过程。”
推荐系统有三个主要组成部分,分别是用户模型、推荐项目模型、推荐算法,推荐系统把用户模型中用户的兴趣或需求信息和推荐项目模型中的特征信息进行匹配,过程中使用相应的推荐算法计算筛选,找出用户可能感兴趣的推荐项目, 然后呈现给用户。

推荐算法是整个推荐系统的核心,可以说推荐算法决定了推荐系统品质的优劣。
主要使用的推荐技术有:基于内容的推荐,协同过滤推荐,基于知识的推荐,基于网络结构的推荐,组合推荐等。目前用的比较多、比较成熟的推荐算法是协同过滤(Collaborative Filtering,简称CF)推荐算法,CF的基本思想是根据用户之前的喜好以及其他兴趣相近的用户的选择来给用户推荐物品。
二.协同过滤算法的简介
目前用的比较多、比较成熟的推荐算法是协同过滤(Collaborative Filtering,简称CF)推荐算法,CF的基本思想是根据用户之前的喜好以及其他兴趣相近的用户的选择来给用户推荐物品。


协同过滤算法的分类:
基于用户的协同过滤推荐(UBCF)
基于项目的协同过滤推荐(IBCF)
基于模型的协同过滤推荐(MBCF)
三.协同过滤推荐算法的流程
计算a和b的相似度时,用sim表示,即,sim(a,b)表示a和b的相似度。
下面介绍相似度计算常用的四个经典算法:余弦定理相似性度量、欧氏距离相似度度量,杰卡德相似性度量和皮尔逊相关系数(Pearson)。
3.1.1余弦定理相似性度量:

3.1.2欧氏距离相似度度量
相对来说,余弦定理体现的是方向上的差异,而欧氏距离更倾向于样本之间的绝对距离,也就是数值上的绝对差异。简单的理解就是,余弦定理受绝对数值影响小,对方向敏感;欧式距离对绝对数值敏感。
比较相似性时,计算的欧式距离越大,表明样本相差的距离越大,也就是相似度越低;计算的欧氏距离越小,表明相似度越高。
3.1.3杰卡德相似系数
杰卡德相似系数一般用J(A,B)表示,有时也写作Jaccard(A,B),其计算公式为:
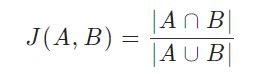
杰卡德相似系数越大,说明相似度越高,当A和B都为空时,J(A,B)=1。
3.1.4.Pearson相关系数
四. UBCF与IBCF
4.1.基于用户的协同过滤推荐(UBCF)
(1)收集历史数据:
显式数据:用户对项目的直接评价,例如用户的评分;
隐式数据:根据用户的行为模式由系统代替用户完成的评价,例如购买记录,用户观看,收藏记录,对评论文本深度的数据挖掘等。
(2)搜索最近邻居:
相似度:相似度越高说明用户越相近,找出与目标用户最相近的若干用户就是这个用户的最近邻;
每个用户对所有项目的评分可看作是一个n维向量(n是项目的总数量),可以用每个n维向量之间的相似度来衡量用户间的相似度。
(3)产生推荐结果:
Top-N推荐:对目标用户未评分的项目中选出其最近邻用户评分值和评分频率最高的前N个项目推荐给目标用户。
(4)优势:
准确率高;避开对项目本身内容进行挖掘
(5)挑战:
用户多的话计算时间就会比较长,新用户问题,数据稀疏性。
(6)注意:
基于用户的协同过滤推荐算法先使用统计技术寻找与目标用户有相同喜好的邻居,然后根据目标用户的邻居的喜好产生向目标用户的推荐。基本原理就是利用用户访问行为的相似性来互相推荐用户可能感兴趣的资源。
基于用户的协同过滤推荐机制的基本原理,假设用户 A 喜欢物品 A、物品 C,用户 B 喜欢物品 B,用户 C 喜欢物品 A 、物品 C 和物品 D;从这些用户的历史喜好信息中,我们可以发现用户 A 和用户 C 的口味和偏好是比较类似的,同时用户 C 还喜欢物品 D,那么我们可以推断用户 A 可能也喜欢物品 D,因此可以将物品 D 推荐给用户 A。
基于用户的协同过滤推荐机制和基于人口统计学的推荐机制都是计算用户的相似度,并基于“邻居”用户群计算推荐,但它们所不同的是如何计算用户的相似度,基于人口统计学的机制只考虑用户本身的特征,而基于用户的协同过滤机制可是在用户的历史偏好的数据上计算用户的相似度,它的基本假设是,喜欢类似物品的用户可能有相同或者相似的口味和偏好。
(7)算法实例:
from operator import *
import math
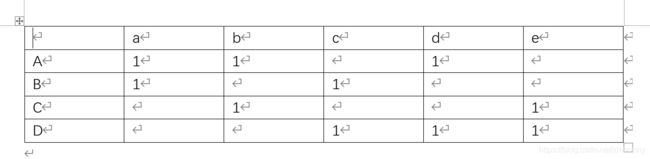
#例子中的数据相当于是一个用户字典{
A:(a,b,d),B:(a,c),C:(b,e),D:(c,d,e)}
#我们这样存储原始输入数据
dic={
'A':('a','b','d'),'B':('a','c'),'C':('b','e'),'D':('c','d','e')}#简单粗暴,记得加''
#计算用户兴趣相似度
def Usersim(dicc):
#把用户-商品字典转成商品-用户字典(如图中箭头指示那样)
item_user=dict()
for u,items in dicc.items():
for i in items:#文中的例子是不带评分的,所以用的是元组而不是嵌套字典。
if i not in item_user.keys():
item_user[i]=set()#i键所对应的值是一个集合(不重复)。
item_user[i].add(u)#向集合中添加用户。
C=dict()#感觉用数组更好一些,真实数据集是数字编号,但这里是字符,这边还用字典。
N=dict()
for item,users in item_user.items():
for u in users:
if u not in N.keys():
N[u]=0 #书中没有这一步,但是字典没有初始值不可以直接相加吧
N[u]+=1 #每个商品下用户出现一次就加一次,就是计算每个用户一共购买的商品个数。
for v in users:
if u==v:
continue
if (u,v) not in C.keys():#同上,没有初始值不能+=
C[u,v]=0
C[u,v]+=1
W=dict()
for co_user,cuv in C.items():
W[co_user]=cuv / math.sqrt(N[co_user[0]]*N[co_user[1]])
return W
def Recommend(user,dicc,W2,K):
rvi=1 #这里都是1,实际中可能每个用户就不一样了。
rank=dict()
related_user=[]
interacted_items=dicc[user]
for co_user,item in W2.items():
if co_user[0]==user:
related_user.append((co_user[1],item))#先建立一个和待推荐用户兴趣相关的所有的用户列表。
for v,wuv in sorted(related_user,key=itemgetter(1),reverse=True)[0:K]:
#找到K个相关用户以及对应兴趣相似度,按兴趣相似度从大到小排列。itemgetter要导包。
for i in dicc[v]:
if i in interacted_items:
continue #书中少了continue这一步吧?
if i not in rank.keys():#如果不写要报错,是不是有更好的方法?
rank[i]=0
rank[i]+=wuv*rvi
return rank
if __name__=='__main__':
W3=Usersim(dic)
Last_Rank=Recommend('A',dic,W3,2)
print(Last_Rank)
4.2基于项目的协同过滤推荐(IBCF)
(1)收集历史数据:(同UBCF)
(2)搜索最近邻居:
相似度:相似度越高说明项目越相近,找出与目标用户最相近的若干项目就是这个用户的最近邻;
每个项目对所有用户的评分可看作是一个m维向量(m是用户的总数量),可以用每个m维向量之间的相似度来衡量用户间的相似度。
(3)产生推荐结果:
Top-N推荐:找出与目标用户感兴趣的项目最相似的Top-N个项目。
(4)优势:
不再考虑用户历史信息;无需进行用户识别;线上推荐效率高。
(5)挑战:
无法满足个性化;新用户问题;数据稀疏性。
(6)注意:
根据所有用户对物品或者信息的评价,发现物品和物品之间的相似度,然后根据用户的历史偏好信息将类似的物品推荐给该用户。
基于项目的协同过滤推荐的基本原理,用户A喜欢物品A和物品C,用户B喜欢物品A、物品B和物品C,用户C喜欢物品A,从这些用户的历史喜好中可以认为物品A与物品C比较类似,喜欢物品A的都喜欢物品C,基于这个判断用户C可能也喜欢物品C,所以推荐系统将物品C推荐给用户C。
基于项目的协同过滤推荐和基于内容的协同过滤推荐都是基于物品相似度预测推荐,只是相似度度量的方法不一样,前者是从用户历史的偏好推断,而后者是基于物品本身的属性特征信息。
from math import sqrt
import operator
import numpy as np
#1.构建用户-->物品倒排
def LoadData(basis_data):
data = {
}
for line in basis_data:
user,score,item = line.split(",")
data.setdefault(user,{
})
data[user][item] = score
print("物品倒排:\n",data)
return data
#2.构建物品与物品的共(同)现矩阵
def similarity(one_data):
#构造物品的共现矩阵
N = {
} #喜欢物品i的总人数
C = {
} #喜欢物品i也喜欢物品j的人数
for user,item in one_data.items():
for i,score in item.items():
N.setdefault(i,0)
N[i] += 1
C.setdefault(i,{
})
for j,scores in item.items():
if j not in i:
C[i].setdefault(j,0)
C[i][j] += 1
print("构造的共现矩阵为:\n{}\n{}".format(N,C))
#计算物品与物品的相似矩阵
W = {
}
for i,item in C.items():
W.setdefault(i,{
})
for j,item2 in item.items():
W[i].setdefault(j,0)
W[i][j] = C[i][j]/sqrt(N[i]*N[j])
print("构造的相似矩阵为:\n",W)
return W
#3.根据用户的历史记录,给用户推荐物品
def recommandList(data,W,user,k,N):
rank={
};
for i,score in data[user].items():#获得用户user历史记录,如A用户的历史记录为{
'a': '1', 'b': '1', 'd': '1'}
for j,w in sorted(W[i].items(),key=operator.itemgetter(1),reverse=True)[0:k]:#获得与物品i相似的k个物品
if j not in data[user].keys():#该相似的物品不在用户user的记录里
rank.setdefault(j,0)
rank[j]+=float(score) * w
sort_data = sorted(rank.items(),key=operator.itemgetter(1),reverse=True)[0:N]
print("推荐为:\n",sort_data)
return sort_data
#主函数
if __name__=='__main__':
#A死侍 B钢铁侠 C美国队长 D黑豹 E蜘蛛侠
#1代表喜欢
user_item_data = ['A,1,a', 'A,1,b', 'A,1,d', 'B,1,b', 'B,1,c', 'B,1,e', 'C,1,c', 'C,1,d', 'D,1,b', 'D,1,c', 'D,1,d','E,1,a', 'E,1,d']
data = LoadData(user_item_data)
W = similarity(data)
#为用户A推荐2部电影
recommandList(data,W,"A",3,2)
4.1.3基于模型的协同过滤推荐(MBCF)
基于用户的协同过滤推荐算法和基于项目的协同过滤推荐算法都是以历史资料为基础,存在的共性问题是资料稀疏以至于在大数据量的条件下实时性差,因此发展了一些以模型为基础的协同过滤。基于模型的协同过滤推荐算法首先根据历史资料建立一个模型,再依据此模型进行推荐。




