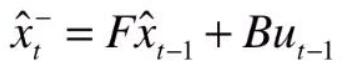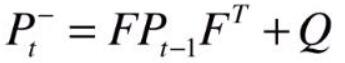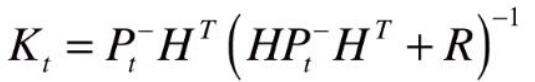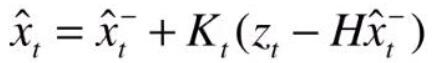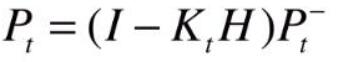卡尔曼滤波算法在FPGA中实现
一、卡尔曼滤波算法
卡尔曼滤波算法是一种基于时域的最佳线性滤波器。卡尔曼滤波器的原理通俗的讲,可以比我们要观测的一个小车的行进速度的过程
小车可能是接近匀速运动的(系统推测)
小车的电机上有一个具有噪声编码器,可以根据编码器计算出当前速度(外界具有噪声的测量数据)
根据上面两个条件我们任意选用一种都可以预测到该时刻小车的速度,但是都包含了很大的噪声,都可以说是小车当前状态的不完全的表现,但是我们通过这两种不完全的表现推测出一个逼近真实的状态,这个过程就是卡尔曼滤波算法的过程。
卡尔曼滤波算法主要是在估计线性系统状态的过程中,以最小均方误差为目的而推导出的几个递推数学等式,主要一共有5个公式,如下式 (1-1)-(1-5)
这五个公式的推导详细请见https://blog.csdn.net/dang_boy/article/details/78419480 在本文就不再赘述了。
二、在MATLAB中验证Kalman滤波算法的五个公式
在这里我们就针对上述的系统做仿真验证,在这里我们根据本系统将卡尔曼的五个公式做一个简化:
首先是预测的两个公式,因为我们的系统预测值就是t-1时刻的系统输出值,所以状态转移矩阵可以直接等效为系数‘1’,我们将式(1-1)简化为式(2-1)。
![]() (2-1)
(2-1)
其次将(1-2)简化为(2-2)。
![]() (2-2)
(2-2)
这里我们将观测矩阵H也当做系数‘1’。将(1-3)简化为(2-3),计算卡尔曼增益
![]() (2-3)
(2-3)
将(1-4)和(1-5)简化为如下(2-4)和(2-5)
![]() (2-4)
(2-4)
![]() (2-5)
(2-5)
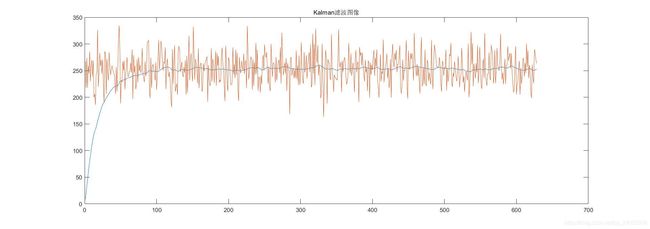
假定1小车以恒定速度前进,MATLAB代码如下(文章结尾附),做出一下曲线见图2-1
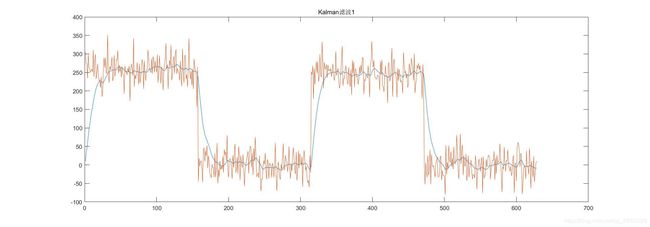
假定2小车速度随时间呈矩形波变化(新手开车^_^)。这时我们需要将(2-1)做一下简单的修改,如下(2_6)。曲线如下图2-2。
![]() (2-6)
(2-6)
三、在FPGA中的实现
笔者在验证FPGA的时候发现手边并没有信号发生器。所以笔者将由MATLAB产生的带走噪声波形储存在ROM里作为测量信号。
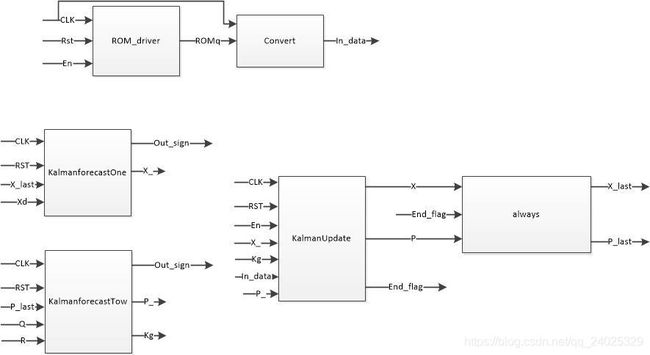
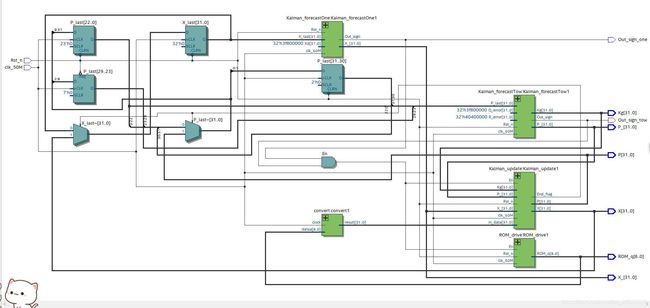
首先根据算法特性,我们画出FPGA的电路结构图,见下图3-1。
笔者将卡尔曼的五个基本公式分成了三个模块。其中KalmanforecastOne包含了公式1,KalmanforcastTow包含了公式2、3,kalmanupdate包含了公式4和公式5。
框架搭建好之后就需要各个模块里面搭建运算单元了。以KalmanforecastOne模块为例。为节省资源,笔者采用线性序列机的方式,控制多项式的计算时序。
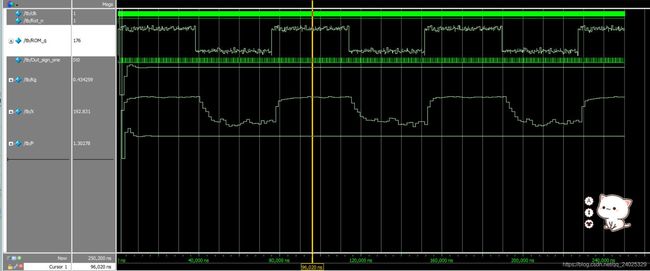
接下来将顶层连线,最后进行功能仿真。RTL视图3-3和仿真结果3-4见下图。
功能仿真图中,ROM_q为ROM中储存的带有噪声的方波信号、Kg为卡尔曼增益、X为滤波后的信号。
四、附录-部分代码
MATLAB代码
clear
clc
t = 1:628;
Z = square(t/50,50);
Z = Z+1.4;
Z = Z*80;
ZZ = randn(1,628);
ZZ = ZZ * 10;
Z = Z+ZZ;
plot(Z);
data = zeros(1,628);
Q = 0.1;
R = 3;
X_last = 0;
P_last = 1;
Dx = 0;
for i=1:628
%X_ = X_last;%预测
X_ = X_last+(X_last-X_last)*0.05;%预测
P_ = P_last +Q;%预测协方差
Kg = P_/(P_+R);%卡尔曼增益
X = X_+Kg*(Z(i)-X_);%估算最优值
P = (1-Kg)*P_;
Dx = X_last;%%保存t-1时刻的X-
P_last = P;
X_last = X;
data(i) = X;
end
plot(t,data,t,Z);KalmanforecastOne文件代码
module Kalman_forecastOne(
clk_50M,
Rst_n,
X_last,
Xd,
Out_sign,
X_
);
input clk_50M;
input Rst_n;
input [31:0]X_last;//输入变量
input [31:0]Xd;//输入变量
output reg [31:0]X_;//输出变量
output reg Out_sign;//计算完成标志
reg [7:0]Count;//序列机基数
reg [31:0]ADD_dataa;
reg [31:0]ADD_datab;
reg ADD_sub;//定义加减标志
wire [31:0]ADD_result;//定义加法器的参数
reg [31:0]MULT_dataa;
reg [31:0]MULT_datab;
wire [31:0]MULT_result;//定义加法器的参数
always@(posedge clk_50M or negedge Rst_n)
if(!Rst_n)
Count <= 1'd0;
else if(Count == 8'd35)
Count <= 1'd0;
else
Count <= Count + 1'd1;
always@(posedge clk_50M or negedge Rst_n)
if(!Rst_n)
Out_sign <= 1'd0;//标志清零
else
begin
case (Count)
8'd1:
begin
Out_sign <= 1'd0;//标志位,开始计算
ADD_sub <= 1'd0;//做减法运算
ADD_dataa<=X_last;
ADD_datab<=Xd;
end
8'd12:
begin
MULT_dataa <= ADD_result;
MULT_datab <= 32'H3F_00_00_00;
end
8'd23:
begin
ADD_dataa <= MULT_result;
ADD_datab <= X_last;
end
8'd34:
begin
X_ <= X_last;//输出公式一的结果
Out_sign <= 1'd1;//标志位,计算完成
end
endcase
end
//==================以下为运算单元==================//
ADD ADD_One1 (
.clock ( clk_50M ),
.add_sub (ADD_sub),
.dataa ( ADD_dataa ),
.datab ( ADD_datab ),
.result ( ADD_result )
);
MULT MULT_One1 (
.clock ( clk_50M ),
.dataa ( MULT_dataa ),
.datab ( MULT_datab ),
.result ( MULT_result )
);
endmodule
FPGA所有代码资料:https://download.csdn.net/download/qq_24025329/11847219
五、总结
算法在MALTAB中实现的还算不错,但是在FPGA仿真中明显可以看出来信号有些失真。ROM是int型需要转换成浮点型,笔者在观察转换输出的时候,在方波的下降沿会出现一个‘+0’不知道是什么原因。这个笔者认为造成波形失真的主要原因。目前笔者正在解决中。
本文为笔者学习笔记,如有纰漏还望各位提出。