1.线性回归-矩阵表达形式
文章目录
- 1. 线性回归-理论知识
- 2. 最小二乘估计:几何意义解释
来自于白板深度学习,感谢up主:https://www.bilibili.com/video/BV1hW41167iL?p=1
1. 线性回归-理论知识
1.1. 数据定义:我们首先定义数据集合 :` D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) } , 其 中 x i ⊆ R p , y i ⊆ R , i = 1 , 2 , . . . . , N D=\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\},其中x_i\subseteq R^p,y_i\subseteq R,i=1,2,....,N D={ (x1,y1),(x2,y2),...,(xN,yN)},其中xi⊆Rp,yi⊆R,i=1,2,....,N,
数据用矩阵表示为:
X = ( x 1 , x 2 , . . . , x N ) T = ( x 1 T x 2 T ⋮ x N T ) = ( x 11 x 12 . . . x 1 p x 21 x 22 . . . x 2 p ⋮ ⋮ ⋮ ⋮ x N 1 x N 2 . . . x N p ) N × P , 其 中 x i 默 认 为 p 维 列 向 量 , 那 么 x i T = ( x i 1 , x i 2 , . . . , x i p ) , X=(x_1,x_2,...,x_N)^T= \begin{pmatrix} x_1^T\\x_2^T\\\vdots\\x_N^T \end{pmatrix}=\begin{pmatrix} x_{11}&x_{12}&...&x_{1p}\\x_{21}&x_{22}&...&x_{2p}\\\vdots&\vdots&\vdots&\vdots\\x_{N1}&x_{N2}&...&x_{Np}\end{pmatrix}_{N \times P},其中x_i默认为p维列向量,那么x_i^T=(x_{i1},x_{i2},...,x_{ip}), X=(x1,x2,...,xN)T=⎝⎜⎜⎜⎛x1Tx2T⋮xNT⎠⎟⎟⎟⎞=⎝⎜⎜⎜⎛x11x21⋮xN1x12x22⋮xN2......⋮...x1px2p⋮xNp⎠⎟⎟⎟⎞N×P,其中xi默认为p维列向量,那么xiT=(xi1,xi2,...,xip),
其中X_i为一个单独的样本集合,一个样本有p个特征。用单独一个列向量表示。
定义数据值Y为: Y = ( y 1 T y 2 T ⋮ y N T ) Y=\begin{pmatrix} y_1^T\\y_2^T\\\vdots\\y_N^T \end{pmatrix} Y=⎝⎜⎜⎜⎛y1Ty2T⋮yNT⎠⎟⎟⎟⎞
设拟合的目标函数: y ^ = f ( w ) = W T x ; ( 为 啥 不 用 W T + b , 因 为 b 可 以 表 示 为 W 0 × ( b 0 = 1 ) 表 示 ) \hat{y}=f(w)=W^Tx;(为啥不用W^T+b,因为b可以表示为W_0\times (b_0=1)表示) y^=f(w)=WTx;(为啥不用WT+b,因为b可以表示为W0×(b0=1)表示)
1.2. 最小二乘法(矩阵表达:几何意义)
1.2.1 用图像表示原始数据和线性回归线的关系:
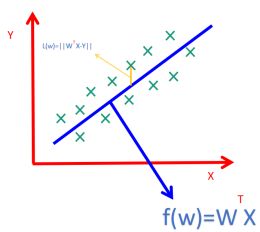
我 们 定 义 损 失 函 数 L ( W ) = ∣ ∣ ∑ i = 1 N W T X i − y i ∣ ∣ 2 = ( ∑ i = 1 N W T X i − y i ) 2 , 我们定义损失函数L(W)=||\sum_{i=1}^{N}W^TX_i-y_i||^2=(\sum_{i=1}^{N}W^TX_i-y_i)^2, 我们定义损失函数L(W)=∣∣∑i=1NWTXi−yi∣∣2=(∑i=1NWTXi−yi)2,我们知道pytorch里面都是矩阵的形式进行运算,所以我们更希望用矩阵形式表示L(W);
L ( W ) = ( w T x 1 − y 1 , w T x 2 − y 2 , . . . , w T x N − y N ) ( w T x 1 − y 1 w T x 2 − y 2 ⋮ w T x N − y N ) L(W)= \begin{pmatrix} w^Tx_1-y_1,w^Tx_2-y_2,...,w^Tx_N-y_N \end{pmatrix}\begin{pmatrix} w^Tx_1-y_1\\w^Tx_2-y_2\\\vdots\\w^Tx_N-y_N \end{pmatrix} L(W)=(wTx1−y1,wTx2−y2,...,wTxN−yN)⎝⎜⎜⎜⎛wTx1−y1wTx2−y2⋮wTxN−yN⎠⎟⎟⎟⎞
= [ ( w T x 1 , w T x 2 , . . . , w T x N ) − ( y 1 , y 2 , . . . y N ) ] ( w T x 1 − y 1 w T x 2 − y 2 ⋮ w T x N − y N ) = [\begin{pmatrix} w^Tx_1,w^Tx_2,...,w^Tx_N \end{pmatrix}-(y_1,y_2,...y_N)]\begin{pmatrix} w^Tx_1-y_1\\w^Tx_2-y_2\\\vdots\\w^Tx_N-y_N \end{pmatrix} =[(wTx1,wTx2,...,wTxN)−(y1,y2,...yN)]⎝⎜⎜⎜⎛wTx1−y1wTx2−y2⋮wTxN−yN⎠⎟⎟⎟⎞
= [ ( w T x 1 , w T x 2 , . . . , w T x N ) − ( y 1 , y 2 , . . . y N ) ] ( w T x 1 − y 1 w T x 2 − y 2 ⋮ w T x N − y N ) = [\begin{pmatrix} w^Tx_1,w^Tx_2,...,w^Tx_N \end{pmatrix}-(y_1,y_2,...y_N)]\begin{pmatrix} w^Tx_1-y_1\\w^Tx_2-y_2\\\vdots\\w^Tx_N-y_N \end{pmatrix} =[(wTx1,wTx2,...,wTxN)−(y1,y2,...yN)]⎝⎜⎜⎜⎛wTx1−y1wTx2−y2⋮wTxN−yN⎠⎟⎟⎟⎞
= [ w T ( x 1 , x 2 , . . . , x N ) − ( y 1 , y 2 , . . . y N ) ] ( w T x 1 − y 1 w T x 2 − y 2 ⋮ w T x N − y N ) = [w^T \begin{pmatrix} x_1,x_2,...,x_N \end{pmatrix}-(y_1,y_2,...y_N)]\begin{pmatrix} w^Tx_1-y_1\\w^Tx_2-y_2\\\vdots\\w^Tx_N-y_N \end{pmatrix} =[wT(x1,x2,...,xN)−(y1,y2,...yN)]⎝⎜⎜⎜⎛wTx1−y1wTx2−y2⋮wTxN−yN⎠⎟⎟⎟⎞
= [ W T X T − Y T ] ( w T x 1 − y 1 w T x 2 − y 2 ⋮ w T x N − y N ) = [W^TX^T-Y^T]\begin{pmatrix} w^Tx_1-y_1\\w^Tx_2-y_2\\\vdots\\w^Tx_N-y_N \end{pmatrix} =[WTXT−YT]⎝⎜⎜⎜⎛wTx1−y1wTx2−y2⋮wTxN−yN⎠⎟⎟⎟⎞
= [ W T X T − Y T ] [ W T X T − Y T ] T = [W^TX^T-Y^T][W^TX^T-Y^T]^T =[WTXT−YT][WTXT−YT]T
= [ W T X T − Y T ] [ X W − Y ] = [W^TX^T-Y^T][XW-Y] =[WTXT−YT][XW−Y]
= W T X T X W − W T X T Y − Y T X W + Y T Y ( 注 : ( W T X T Y ) T = Y T X W ) =W^TX^TXW-W^TX^TY-Y^TXW+Y^TY(注:(W^TX^TY)^T=Y^TXW) =WTXTXW−WTXTY−YTXW+YTY(注:(WTXTY)T=YTXW)
= W T X T X W − W T X T Y − Y T X W + Y T Y =W^TX^TXW-W^TX^TY-Y^TXW+Y^TY =WTXTXW−WTXTY−YTXW+YTY
= W T X T X W − W T X T Y − Y T X W + Y T Y =W^TX^TXW-W^TX^TY-Y^TXW+Y^TY =WTXTXW−WTXTY−YTXW+YTY
= W T X T X W − 2 W T X T Y + Y T Y =W^TX^TXW-2W^TX^TY+Y^TY =WTXTXW−2WTXTY+YTY
综 上 所 述 L ( W ) = W T X T X W − 2 W T X T Y + Y T Y 综上所述 L(W)=W^TX^TXW-2W^TX^TY+Y^TY 综上所述L(W)=WTXTXW−2WTXTY+YTY L(W)对W进行矩阵求导可得:
∂ ∂ W L ( W ) = 2 X T X W − 2 X T Y + 0 = 2 X T X W − 2 X T Y = 0 \frac{\partial}{\partial}^{L(W)}_{W}=2X^TXW-2X^TY+0=2X^TXW-2X^TY=0 ∂∂WL(W)=2XTXW−2XTY+0=2XTXW−2XTY=0 由此可得: W ^ = a r g m i n ( L ( W ) ) = ( X T X ) − 1 X T Y \hat{W}=argmin(L(W))=(X^TX)^{-1}X^TY W^=argmin(L(W))=(XTX)−1XTY;重点结论!!! W ^ = ( X T X ) − 1 X T Y \hat{W}=(X^TX)^{-1}X^TY W^=(XTX)−1XTY
2. 最小二乘估计:几何意义解释
2.1 由于X 为 X = ( x 1 , x 2 , . . . , x N ) T = ( x 1 T x 2 T ⋮ x N T ) = ( x 11 x 12 . . . x 1 p x 21 x 22 . . . x 2 p ⋮ ⋮ ⋮ ⋮ x N 1 x N 2 . . . x N p ) N × P X=(x_1,x_2,...,x_N)^T= \begin{pmatrix} x_1^T\\x_2^T\\\vdots\\x_N^T \end{pmatrix}=\begin{pmatrix} x_{11}&x_{12}&...&x_{1p}\\x_{21}&x_{22}&...&x_{2p}\\\vdots&\vdots&\vdots&\vdots\\x_{N1}&x_{N2}&...&x_{Np}\end{pmatrix}_{N \times P} X=(x1,x2,...,xN)T=⎝⎜⎜⎜⎛x1Tx2T⋮xNT⎠⎟⎟⎟⎞=⎝⎜⎜⎜⎛x11x21⋮xN1x12x22⋮xN2......⋮...x1px2p⋮xNp⎠⎟⎟⎟⎞N×P ,那么我们可以把X按照一列为一个向量表示 X = ( X 1 , X 2 , . . . , X p ) X=(X_1,X_2,...,X_p) X=(X1,X2,...,Xp)那么 f ( w ) = W T X = X T β f(w)=W^TX=X^T\beta f(w)=WTX=XTβ,那么就形成了有P维组成的向量空间(注:空间S 由一组维度为P的基组成),那么最小二乘法可以看做是向量Y到向量空间S的最短距离,如图所示:
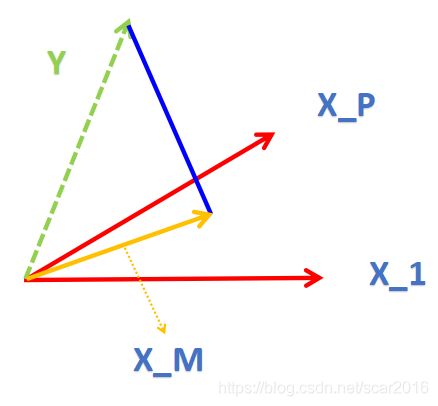
向 量 X M 由 向 量 空 间 X 1 , . . . , X p 组 成 , 由 图 可 得 , 最 短 距 离 应 该 是 向 量 Y 向 空 间 S 做 的 垂 线 距 离 [ 投 影 ] , X M = X ⃗ β ⃗ 向量X_M由向量空间X_1,...,X_p组成,由图可得,最短距离应该是向量Y向空间S做的垂线距离[投影],X_M=\vec X\vec\beta 向量XM由向量空间X1,...,Xp组成,由图可得,最短距离应该是向量Y向空间S做的垂线距离[投影],XM=Xβ
法向量可表示 a ⃗ = ( Y ⃗ − X ⃗ β ⃗ ) , 由 于 法 向 量 a ⃗ 垂 直 于 S 空 间 , 所 以 a ⃗ T X = 0 \vec a=(\vec Y-\vec X\vec\beta),由于法向量\vec a垂直于S空间,所以\vec a^T X=0 a=(Y−Xβ),由于法向量a垂直于S空间,所以aTX=0,综上所述:
X ⃗ T ( Y ⃗ − X ⃗ β ⃗ ) = 0 ⃗ \vec X^T(\vec Y-\vec X\vec\beta)=\vec0 XT(Y−Xβ)=0展开上公式可得: X T Y = X T X β , 所 以 β = ( X T X ) − 1 X T Y X^TY=X^TX\beta,所以 \beta=(X^TX)^{-1}X^TY XTY=XTXβ,所以β=(XTX)−1XTY;居然跟上面矩阵求导的结果一模一样,向量形式更加的形象。