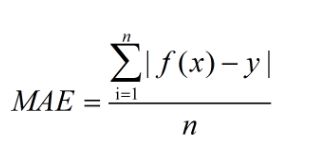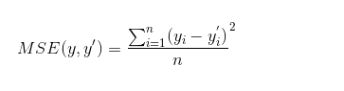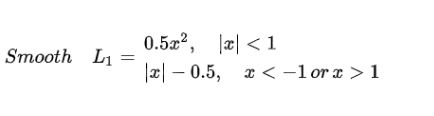【必知必会】2021最详细深度学习损失函数盘点【一】L1Loss、L2Loss、Smooth L1 Loss
文章目录
- 0 前言:
- 1 定义
- 2 特点
- 3 常见的经典误差函数
-
- 3.1 平均绝对误差MAE(L1 Loss)
-
- 公式:
- 图像:
- 优点
- 缺点
- 应用场景:
- Pytorch示例:
- 3.2 均方误差MSE(L2 Loss)
-
- 公式:
- 图像:
- 优点
- 缺点
- 应用场景:
- pytorch示例:
- 3.3 Smooth L1损失
-
- Paper:
- 公式:
- 对比L1、L2图像:
- Smooth L1优点:
- Pytorch设计Smooth_L1_loss:
- 3.4 Binary Cross Entropy Loss(二分类交叉熵)
- 3.5 Cross Entropy Loss交叉熵损失
-
- 意义:
- 公式:
- 图像:
- 应用场景
- Pytorch示例:
- 3.6 Softmax Loss
-
- 公式及推导:
- 图像:
- 应用场景:
- 代码实现:
- 3.7 机器学习中损失函数的选取方法
- 4、Falcal_loss
- 5、GHM_loss
- 6、IOU_loss系列
-
-
- 6.1 IoU Loss
-
- IoU及 L2 Loss 对比:
- 问题
- 6.2 GIoU Loss
-
- Paper:
- 6.3 DIoU Loss
-
- Paper:
- 定义:
- 优点:
-
- 7、人脸系列loss
-
- 7.1 DeepID系列双约束的Loss
- 7.2 Facenet的Triplet Loss
- 7.3 SphereFace的L-Softmax loss
- 7.4 Center_loss
- 7.5 COCO loss
- 7.6 L2-Softmax loss
- 7.7 Additive Margin Loss
- 7.8 CosFace
- 7.9 ArcFace
- 8、推荐Paper:
0 前言:
菜鸡要水文,那损失函数这个模块肯定少不了,手动狗头,洋洋洒洒水了不少文字,文章盘点的知识点涵盖比较大,抛砖引玉了。毕竟这些点的随便一个点都足以写一篇详细解读博文,为了方便感兴趣的同学请继续深挖,都清晰的附出了,源论文及代码的出处,当然网上也有不少大佬写了详细知识点博文可以参考。
1 定义
损失函数(误差函数)是关于模型输出和样本标签值之差的函数,通过对误差函数求导来调节权重参数。
本质:选取恰当的函数来衡量模型输出分布和样本标签分布之间的接近程度。
注:损失函数的基本要求是用来衡量模型输出分布和样本标签分布之间的接近程度,高级需求是在样本分布不均匀地情况下,精确地描述模型输出分布和样本标签之间的接近程度。
损失函数分为经验风险损失函数和结构风险损失函数。经验风险损失函数指预测结果和实际结果的差别,结构风险损失函数是指经验风险损失函数加上正则项。
通俗的理解,我们常用Loss来评价模型的预测值和真实值不一样的程度,损失函数越好,通常模型的性能越好。不同的模型用的损失函数一般也不一样。
误差函数的选择,不仅与要解决的问题有关,而且也和激活函数有关,然后通过对误差函数求导,利用BP调节模型中的所有参数。
2 特点
- 凸函数,才能用于找到函数的最小值。
- 每一点都可导,可导才能通过BP算法完成对权重参数的调节。
- BP算法的目的,就是求能够使误差函数取得最小值对应的权重参数,因此,误差函数求导以后,极值点对应的权重参数就是最优解,极值点的导数为0,参数不再更新,找到了最优解。这也是梯度下降法寻找最优解的原理。
3 常见的经典误差函数
3.1 平均绝对误差MAE(L1 Loss)
公式:
MAE是指模型预测值f(x)和真实值y之间距离的平均值,公式如下:
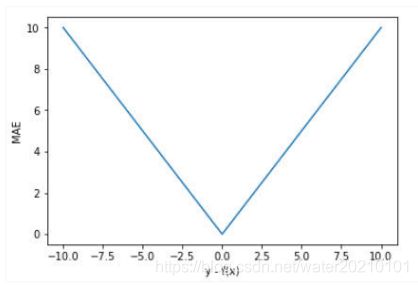
图像:
图1
优点
相比于MSE,MAE有个优点就是,对于离群点不那么敏感。因为MAE计算的是误差(y-f(x))的绝对值,对于任意大小的差值,其惩罚都是固定的。无论对于什么样的输入值,都有着稳定的梯度,不会导致梯度爆炸问题,具有较为稳健性的解。
缺点
MAE曲线连续,但是在(y-f(x)=0)处不可导。而且 MAE 大部分情况下梯度都是相等的,这意味着即使对于小的损失值,其梯度也是大的。这不利于函数的收敛和模型的学习。
应用场景:
Pytorch示例:
>>> loss = nn.L1Loss()
>>> input = torch.randn(3, 5, requires_grad=True)
>>> target = torch.randn(3, 5)
>>> output = loss(input, target)
>>> output.backward()
3.2 均方误差MSE(L2 Loss)
公式:
上式中,yi为一个batch中第 i 个数据的正确答案,yi`为神经网络给出的预测值。
MSE是求一个batch(一批的数据)的平均误差的函数。
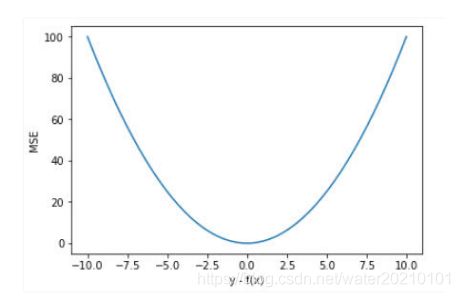
图像:
见上图蓝色实线
优点
MSE的函数曲线光滑、连续,处处可导,便于使用梯度下降算法,是一种常用的损失函数。 而且,随着误差的减小,梯度也在减小,这有利于收敛,即使使用固定的学习速率,也能较快的收敛到最小值。
缺点
当真实值y和预测值f(x)的差值大于1时,会放大误差;而当差值小于1时,则会缩小误差,这是平方运算决定的。MSE对于较大的误差(>1)给予较大的惩罚,较小的误差(<1)给予较小的惩罚。也就是说,对离群点比较敏感,受其影响较大。
如果样本中存在离群点,MSE会给离群点更高的权重,这就会牺牲其他正常点数据的预测效果,最终降低整体的模型性能。 如下图:
应用场景:
主要用于回归问题,不用于分类。
交叉熵的损失函数只和分类正确的预测结果有关系,而MSE的损失函数还和错误的分类有关系,该分类函数除了让正确的分类尽量变大,还会让错误的分类变得平均,但实际在分类问题中这个调整是没有必要的。但是对于回归问题来说,这样的考虑就显得很重要了。所以,回归问题熵使用交叉上并不合适。
pytorch示例:
loss_fn = torch.nn.MSELoss(reduce=False, size_average=False)
loss = loss_fn(input.float(), target.float())
3.3 Smooth L1损失
Paper:
在Faster R-CNN以及SSD中对边框的回归使用的损失函数都是Smooth L1 作为损失函数。
公式:
smooth L1损失函数为:
smooth L1说的是光滑之后的L1,前面说过了L1损失的缺点就是有折点,不光滑,导致不稳定,那如何让其变得光滑呢?
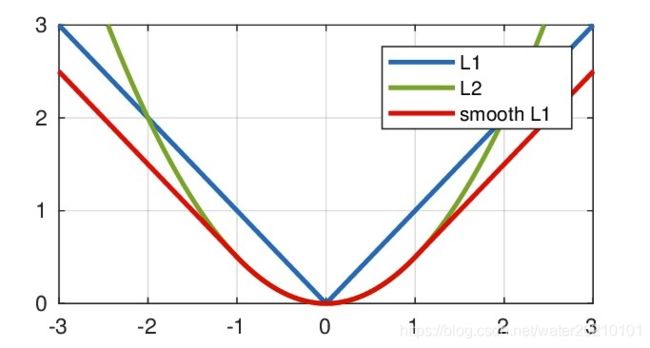
对比L1、L2图像:
红色实线为Smooth L1
对于大多数CNN网络,我们一般是使用L2-loss而不是L1-loss,因为L2-loss的收敛速度要比L1-loss要快得多。
对于边框预测回归问题,通常也可以选择平方损失函数(L2损失),但L2范数的缺点是当存在离群点的时候,这些点会占loss的主要组成部分。比如说真实值为1,预测10次,有一次预测值为1000,其余次的预测值为1左右,显然loss值主要由1000决定。
所以FastRCNN采用稍微缓和一点绝对损失函数(smooth L1损失),它是随着误差线性增长,而不是平方增长。
Smooth L1 和 L1 Loss 函数的区别在于:
L1 Loss 在0点处导数不唯一,可能影响收敛。Smooth L1的解决办法是在 0 点附近使用平方函数使得它更加平滑。
Smooth L1优点:
- 相比于L1损失函数,可以收敛得更快。
- 相比于L2损失函数,对离群点、异常值不敏感,梯度变化相对更小,训练时不容易跑飞。
Pytorch设计Smooth_L1_loss:
import torch
import torch.nn.functional as
def smooth_l1_loss(a, b):
loss_part1 = torch.abs(a - b)
loss_part2 = loss_part1 ** 2
loss_part2 = loss_part2 * 0.50
loss2 = torch.where(loss_part1 >= 1, loss_part1 - 0.5, loss_part2)
#统计每个预测框的loss
#loss2 = torch.sum(loss2, dim = 1)
#返回所有预测框的loss
loss2 = torch.sum(loss2)
return loss2
def test_smmoth_l1_loss():
loc_p = torch.tensor([1, 5, 3, 0.5])
loc_t = torch.tensor([4, 1, 0, 0.4])
loss_1 = F.smooth_l1_loss(loc_p, loc_t, size_average=False)
print ("F.smooth_l1_loss:", loss_1)
loss_2 = smooth_l1_loss(loc_p, loc_t)
print ("smooth_l1_loss:", loss_2)
3.4 Binary Cross Entropy Loss(二分类交叉熵)
3.5 Cross Entropy Loss交叉熵损失
意义:
公式:
图像:
应用场景
Pytorch示例:
loss_func = torch.nn.CrossEntropyLoss()
loss = loss_func(output, labels) # 样本标签值必须是一维向量
3.6 Softmax Loss
公式及推导:
图像:
应用场景:
代码实现:
3.7 机器学习中损失函数的选取方法
4、Falcal_loss
5、GHM_loss
6、IOU_loss系列
6.1 IoU Loss
IoU及 L2 Loss 对比:
问题
6.2 GIoU Loss
Paper:
6.3 DIoU Loss
Paper:
定义:
优点:
7、人脸系列loss
人脸检测识别是计算机视觉里研究比较早比较成熟的了,但是却也是个比较复杂的系统,包括人脸检测、人脸对齐、人脸映射与人脸识别、LOSS的设计等等,不是1-2篇文章可以说的清楚的,这个系列里只是抛砖引玉,欢迎后续留言交流学习。
7.1 DeepID系列双约束的Loss
7.2 Facenet的Triplet Loss
Triplet Loss这个是工业界使用较多引用量最高的人脸loss了。Triple Loss,以三元组形式进行优化,获得类内紧凑和类间差异。
7.3 SphereFace的L-Softmax loss
SphereFace是L-Softmax的改进,归一化了权值W,让训练更加集中在优化深度特征映射和特征向量角度上,降低样本数量不均衡问题
7.4 Center_loss
7.5 COCO loss
归一化了权值c,归一化了特征f,并乘尺度因子,在LFW上达到99.86%