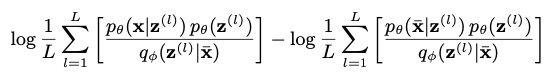《异常检测——从经典算法到深度学习》12 对于复杂 KPI 基于VAE对抗训练的非监督异常检测
《异常检测——从经典算法到深度学习》
- 0 概论
- 1 基于隔离森林的异常检测算法
- 2 基于LOF的异常检测算法
- 3 基于One-Class SVM的异常检测算法
- 4 基于高斯概率密度异常检测算法
- 5 Opprentice——异常检测经典算法最终篇
- 6 基于重构概率的 VAE 异常检测
- 7 基于条件VAE异常检测
- 8 Donut: 基于 VAE 的 Web 应用周期性 KPI 无监督异常检测
- 9 异常检测资料汇总(持续更新&抛砖引玉)
- 10 基于条件 VAE 的鲁棒无监督KPI异常检测
- 11 针对大量出现的KPI流快速部署异常检测模型
- 12 对复杂 KPI 基于VAE对抗训练的非监督异常检测
12 对于复杂 KPI 基于VAE对抗训练的非监督异常检测
2019 Unsupervised Anomaly Detection for Intricate KPIs via Adversarial Training of VAE
下载地址
一直在纠结有没有必要这么这么地翻译一遍,是否有意义,是否真的有人会读。所以从这篇论文开始,去除了一些套话,尽可能更加突出重点。
Abstract
为了保证互联网应用服务的可靠性,我们需要实时地密切监测 KPIs,并必须及时发现 KPIs 中隐藏的异常。尽管对于周期性光滑的业务级别的 KPIs (例如每分钟的交易次数) 的异常检测在文献中已经被合理地解决了,但是机器级别的 复杂的 KPIs(例如一个被检测的服务每秒的 I/O 请求数)很少研究。这些复杂的 KPIs 既普遍又重要,但是它们呈现的是非高斯分布、很难建模的数据分布。本文中,我们提出了一个基于局部分析的贝叶斯网络的对抗性训练方法,这种方法具有坚实的理论证明。基于这个方法,我们提出了第一个针对于复杂的 KPIs的高性能无监督异常检测算法 Buzz。在来自一家全球互联网公司的数据中它的 最优 F-score 范围在0.92到0.99之间,显著优于基于最先进VAE的无监督方法(无对抗性训练)和最先进的有监督方法。
I. Introduction
略去前面一部分与 Abstract 基本重合的部分
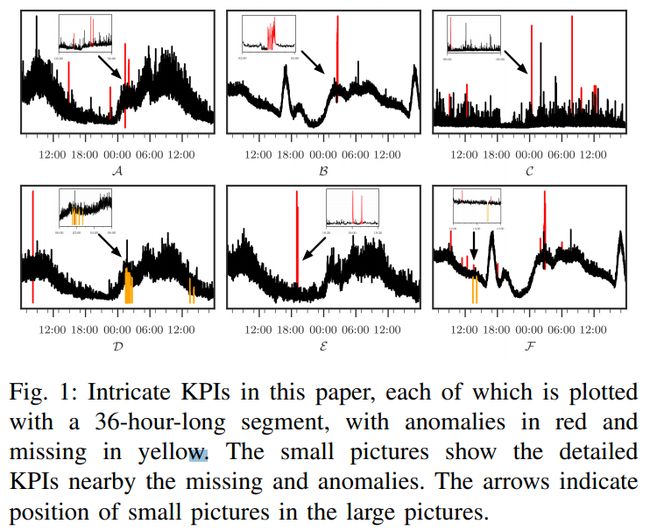
图 1 展示了几个这类的 KPI,Opprentice[3](最先进的监督方法)和Donut [4] (一种基于变分自动编码器(VAE)的先进无监督方法)性能不佳,将在第5节展示。
Buzz 有几个关键idea。首先,为了使不可分割的 KPI 模型易于处理,我们采用了度量理论中常用的分析方法。具体而言,我们将数据空间切分为若干个子空间(隔离的)。其次,在计算距离时,我们使用了生成分布和经验分布之间的Wasserstein距离[6],这在 WGAN[6] 中已经被证明是分布空间中的一个稳健(robust)度量。
第三,我们提供理论推导,提出了一种训练目标的基本形式,然后将我们的模型转化为贝叶斯网络。特别是,Buzz 通过对抗训练,从本质上优化了 VAE 中变分的最低证据界(ELBO) 似然。第四,我们使用 VAE 作为生成模型来生成样本,并使用另外一种神经网络作为判别模型来识别生成的样本和真实样本。第五,为了保证对抗训练稳定,我们调整了梯度惩罚技术[7],一种从 WGAN[6] 的基本训练的改进技术。最后,异常检测是采用变分推断来完成的。
Buzz 的 contribution 总体如下:
- Buzz 是针对于复杂 KPIs 的第一个通过深度生成模型无监督异常检测算法。在全球顶级公司的数据中,Buzz 的最优 F-score 在 0.92 到 0.99 之间,显著优于现有方法。
- Buzz 提出的训练方法是第一种基于分区的VAE对抗性训练方法理论推导与实验分析相结合。
- 基于分区分析,我们提出了一种基于 Wasserstein 距离的 Buzz 训练目标的初始形式,并给出了将该模型转化为贝叶斯网络的理论推导。在贝叶斯网络和最优运输理论之间架起桥梁是一种新的思路。
2. Background
A. KPI Anomaly Detection
一个 KPI 是一个时间序列,可以标记为: X = { x 1 , x 2 , . . . , x T } X=\{x_1,x_2,...,x_T\} X={ x1,x2,...,xT},其中 x t x_t xt 是指对应 t t t 时刻的值, t ∈ { 1 , 2 , . . , T } t\in\{1,2,..,T\} t∈{ 1,2,..,T}。
基于 KPI 的异常检测即给定最近的 W W W 个数据点,来判定 x t x_t xt 是不是异常。如果是异常的话, α t = 1 \alpha_t=1 αt=1。异常检测算法通常计算条件概率, P ( α t = 1 ∣ X t − W + 1 , . . . , x t ) P(\alpha_t=1|X_{t-W+1},...,x_t) P(αt=1∣Xt−W+1,...,xt),而不是直接给定 α t \alpha_t αt 的值。因此,基本上任何 KPI 异常检测苏阿帆需要对条件概率进行一些建模。
B. Intricate KPIs
本文中,我们注重对复杂 KPIs 的异常检测。 KPIs 大概分为两类:周期性光滑 KPIs 和 复杂 KPIs。前者一般是基于服务/业务层的分析(比如每分钟的交易数目)。我们可以粗略地假设这些 KPI 具有对角多元高斯噪声(diagonal multivariate Gaussian noises)。为了捕捉突发流量(例如,典型的数据库流量)引起的微拥塞,经常复杂 KPIs 进行细粒度监控。我们可以粗略地假设复杂 KPIs 中的噪声不是对角多元高斯噪声。
图1 展示了一些复杂 KPIs 例子。可以看到,复杂的 KPIs 是复杂的,在短时间尺度上剧烈抖动,但在全球范围内似乎有一些模式。此外,不同的复杂 KPIs 可以具有不同的全局和局部模式。因此,精确定义复杂的 KPIs 或列举不同类型的复杂 KPIs 具有挑战性。因此,设计一个框架并测试所有复杂的 KPIs 是很难的。因此,在本文中,我们将重点放在复杂的关键绩效指标,我们反击,并在实践中很重要。更具体地说,我们从一家具有手动异常标签的大型互联网公司获得 11 个维护良好的复杂 KPIs,图1 显示了其中的一部分。它们代表了一系列重要、实用和复杂的 KPIs。与我们合作的操作人员证实,解决这些复杂的 KPIs 异常检测问题具有迫切的现实意义。
C. Previous Anomaly Detection Approaches
多年来,人们提出了许多基于传统统计模型的异常检测器,如 [8] 等人 [9]-[14],但算法选择和参数调整需要在每个 KPI 的基础上进行,它们无法在复杂的 KPIs 中捕获复杂的数据分布。
最近的方法使用了有监督集成学习和上述检测器作为特征,如 EGADS[15] 和 Opprentice [3],并在平滑 KPI 上显示了有希望的结果。但是,它们的标记开销太大,并且它们的特征(来自传统统计模型)不适合复杂的 KPI。
无监督异常检测方法,如 [16]-[20] 学习获取正常数据模式并推导条件概率 P ( α t = 1 ∣ x t − w + 1 , x t − W + 2 , . . . , x t ) P(\alpha_t=1|x_{t-w+1}, x_{t-W+2},...,x_{t}) P(αt=1∣xt−w+1,xt−W+2,...,xt),通过假设异常,例如异常的可能性可以忽略不计。Donut [4] 是最先进的无监督异常检测方法。它以VAE [21]、[22] 为基础,对周期性平滑 KPI 表现出高性能、并且具有扎实的理论分析。但由于 Donut 假设为对角多元高斯噪声,因此它在复杂的 KPI 上表现不佳,如 图9 所示。
D. Variational Auto-Encoder
VAE [21],[22] 是一个深度贝叶斯网络,它对两个随机变量 x x x 和 z z z 之间的关系进行建模。 p ( x ) p(x) p(x) 称为经验分布, p ( z ) p(z) p(z) 称为先验分布,通常为多元标准高斯分布 N ( 0 , I ) \mathcal{N}(0,I) N(0,I)。 条件分布 p θ ( x ∣ z ) p_\theta(x|z) pθ(x∣z) 的形式是根据任务的特定要求来选择。然后, p θ ( x ) = E p ( z ) [ p θ ( x ∣ z ) ] p_\theta(x)=\mathbb{E}_{p(z)}[p_{\theta}(x|z)] pθ(x)=Ep(z)[pθ(x∣z)] 可以看作是一种核密度估计(kernel density estimation)。 q ϕ ( z ∣ x ) q_\phi(z|x) qϕ(z∣x) 是对计算困难的真实后验 p θ ( z ∣ x ) p_\theta(z|x) pθ(z∣x) 的后验似然。 q ϕ ( z ∣ x ) q_\phi(z|x) qϕ(z∣x) 可以通过神经网络,利用 SGVB 算法,通过对最大化 证据下界(ELBO)的似然估计进行拟合。
VAE 的训练目标,记作 L v a e \mathcal{L}_{vae} Lvae,即 E p ( x ) [ log p θ ( x ) ] \mathbb{E}_{p(x)}[\log_{p_\theta}(x)] Ep(x)[logpθ(x)] 的 ELBO。
L v a e = E p ( x ) [ E q ϕ ( z ∣ x ) [ log p θ ( x ∣ z ) ] − K L [ q ϕ ( z ∣ x ) ∣ ∣ p θ ( z ) ] ] \mathcal{L}_{vae}=\mathbb{E}_{p(x)}[\mathbb{E}_{q_\phi(z|x)}[\log {p_\theta(x|z)}]-KL[\ q_\phi(z|x)\ ||\ p_\theta(z)]] Lvae=Ep(x)[Eqϕ(z∣x)[logpθ(x∣z)]−KL[ qϕ(z∣x) ∣∣ pθ(z)]]
Donut [4] 修改了 ELBO 的一部分,以避免训练中异常的影响,并在周期性平滑 KPI 上取得了较高的性能。但是,Donut 在复杂的 KPI 上工作得不好 —— 我们对 Donut 进行了多次训练,发现 Donut 的性能很低,不稳定,而且没有经过良好的训练(将在第5节中显示)。我们推测,由于神经网络表达能力和训练方法的限制,很难在复杂的经验分布 p ( x ) p(x) p(x) 上进行训练,并且训练样本有限,如 图8 所示。
E. Adversarial Training
文献中已经提出了一系列对抗性训练方法,如 GAN [23]、WGAN [6]、AAE [24]、WAE [25] 和 GAN-OT [26]。在对抗训练中,生成器模型试图生成样本来欺骗鉴别器模型,鉴别器试图区分生成的样本和真实样本。在对抗训练中,发生器和鉴别器的能力都有很大的提高。在图像分类、图像生成、语音识别等领域,对抗训练在复杂的经验分布上取得了很好的效果。
有几项关于 VAE 和高级训练相结合的研究,如 [27],与我们的结构看起来是相似的,但我们的理论证明表明它们在本质上是完全不同的。AAE[24] 提出了一种基于先验分布 p ( z ) p(z) p(z) 的对抗性训练方法,具有较高的性能和可靠的证明。受此启发,本文提出了一种复杂经验分布 p ( x ) p(x) p(x) 的VAE对抗训练方法。在此基础上,提出了一种基于深层生成模型的复杂 KPI 异常检测算法。
3. Architecture
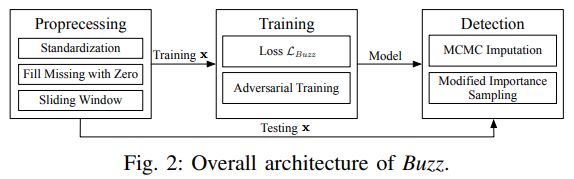
在本节中,我们将介绍我们的动机和提出的异常检测框架 Buzz ,包括预处理阶段、训练目标和相应的算法、神经网络结构以及检测方法。总体架构如 图2 所示。
A. Motivation
Buzz 有两个主要观点:Wasserstein 距离和与测量理论的分离(Partitioning from measure theory.)。
在计算距离时,我们使用了生成分布和经验分布之间的Wasserstein距离[6](以下称为分布距离),WGAN[6]表明,在测量概率分布之间的距离时,该距离是稳健的。
Partitioning 是测度论中一种强大且常用的分布分析方法[28],[29]。其基本思想本质上类似于微积分中的一种常见技术:在计算一个复杂函数的积分时,通常把它的积分域分成若干个分区,然后计算每个分区上的积分,然后求其平均值。同样地,我们将具有复杂经验分布的空间 X \mathcal{X} X 划分为几个分区,直观地说,在每个足够小的分区上计算分布距离可能比在整个空间上更容易。
每个分区上的分布距离是通过对抗训练计算出来的,全局距离是所有分区上分布距离的期望值,如 图3 所示。
巧合的是,我们注意到,当每个分区越来越小时,全局距离接近 VAE 的一个特殊变量的 ELBO 中的重构项,其后验分布是指数分布(an exponential distribution)。分区(Potition)在分区从整体到点的变化过程中起着连接 WGAN 和 VAE 的损失的作用。它启发了我们对抗性的VAE训练方法。
我们将对这一动机进行理论推导,并在第4节中给出一个近似的训练目标。 在本节中,我们将首先演示它在实践中是如何工作的。
B. Preprocessing
实际应用中的 KPIs 是复杂的时间序列数据。有时监视器不会捕获某个值并将其设置为 NaN,称为缺失值。有时,在一段时间内,价值观的规模都非常大。这些值会给训练和检测带来困难,因此需要对数据进行预处理。
首先,我们将缺失的值设置为零,然后分割数据将 KPI 分为训练集和测试集。其次,我们计算训练集中的均值 μ \mu μ 和标准差 σ \sigma σ 。第三,我们对数据进行标准化,即将每个数值 x x x 设为 ( x − μ ) σ { {(x-\mu)}\over{\sigma}} σ(x−μ) 。第四,我们将标准值截断在 [−10, 10] 之间。
我们的模型的输入是来自标准化 KPI 的滑动窗口,每个窗口是 W W W长的时间序列段,其中 W W W是一个称为窗口大小的超参数。在时间 t t t 结束的窗口表示为 x ( t ) x^{(t)} x(t) 窗口 { x t − W + 1 , . . . , x t x_{t-W+1},...,x_t xt−W+1,...,xt} 中的值记录为 x k ( t ) x_k^{(t)} xk(t)。
C. Neural Network
我们的模型由 3 个子网络组成:变分网络(the variational network)、生成网络 (the generative network) 和判别网络(the discriminative network),如 图4a、图4b、图4c 中所示。
变分网络的设计是为了找到与给定的窗口 x x x 对应的 q ϕ ( z ∣ x ) q_\phi(z|x) qϕ(z∣x) 。我们将窗口 reshape 为 2 维矩阵,使用卷积层 [30] 来提取高级别的特征,记作 h z ( x ) h_z(x) hz(x)。然后我们分离 q ϕ ( z ∣ x ) q_\phi(z|x) qϕ(z∣x) 中的均值和标准差: μ z ( x ) = W μ z T ⋅ b μ z \mu_z(x)=W^T_{ {\mu}_z} \cdot b_{\mu_z} μz(x)=WμzT⋅bμz , σ z ( x ) = S o f t P l u s ( W σ z T ) ⋅ h z ( x ) + b σ z ) + ϵ \sigma_{z}(x)=SoftPlus(W^T_{\sigma_z})\cdot h_z(x)+b_{\sigma_z})+\epsilon σz(x)=SoftPlus(WσzT)⋅hz(x)+bσz)+ϵ ,其中 ϵ \epsilon ϵ 是一个正的向量常数。
生成网络的设计是为了由变分网络得到的 q ϕ ( z ∣ x ) q_\phi(z|x) qϕ(z∣x) 生成重构窗口。我们通过一个全连接层将 z z z 映射到 2维矩阵,然后通过一系列二维转置到卷积层,最后 reshape 为 1 维数据,从而得到重构窗口 G ( z ) G(z) G(z)。
判别网络的设计是为了从重构窗口 y \mathcal{y} y 中检测出真实窗口 x x x 。我们将窗口 reshape 为 2 维,通过卷积层获得高级别的特征,将这些特征传递到一个全连接层,最后获得判别器的输出 F ( x ) F(x) F(x)。
D. Training Objective
Buzz 最重要的部分是它的训练目标。我们为复杂 KPIs 提出了一个新的训练目标 L ~ B u z z \mathcal{\widetilde L}_{Buzz} L Buzz ,以解决在数据集上很难使用纯贝叶斯下界(如 Donut 方法)来训练模型的问题(参见第5节)。 L ~ B u z z \mathcal{\widetilde L}_{Buzz} L Buzz 的准确定义和推导在第4节中给出。这个章节,我们只给出 L ~ B u z z \mathcal{\widetilde L}_{Buzz} L Buzz 的采样格式和它的训练算法。
符号 s , b s, b s,b 是参数,表示邻域大小和批量大小。设 W \mathcal{W} W 为 { w 1 , w 2 , . . , w b \mathcal{w}_1,\mathcal{w}_2,..,\mathcal{w}_b w1,w2,..,wb},即随机选择时间的一个小批量,满足:每一个 w i w_i wi 都是 s s s 的倍数,并且 $w_i \ne w_j $ ∀ i ≠ j i\ne j i=j。我们把 W \mathcal{W} W 上的这个条件称为领域条件(Neighbor Condition,NC)。 w ∈ W w\in \mathcal{W} w∈W 的领域集合为 { w , w + 1 , . . . , w + s − 1 w,w+1,...,w+s-1 w,w+1,...,w+s−1},这是一个分区的时间。 x ( w ) , x ( w + 1 ) , . . . , x ( w + s − 1 ) x^{(w)},x^{(w+1)},...,x^{(w+s-1)} x(w),x(w+1),...,x(w+s−1) 的多面体单元的联合是 X \mathcal{X} X 的一个分区 S w S_w Sw。这个一个简单高效的分区方法。定义符号:
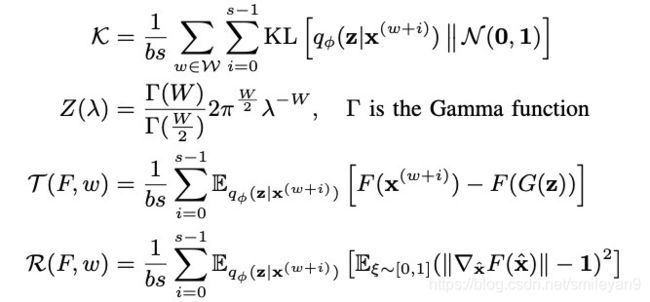
其中 x ^ \hat x x^ 是指 ξ x w + i + ( 1 − ξ ) G ( z ) \xi x^{w+i}+(1-\xi)G(z) ξxw+i+(1−ξ)G(z)。然后训练目标 L ~ B u z z \mathcal{\widetilde L}_{Buzz} L Buzz 为:
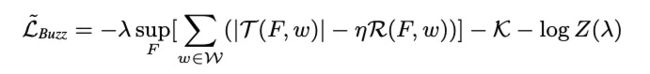
L ~ B u z z \mathcal{\widetilde L}_{Buzz} L Buzz 是 一种特殊的对抗训练算法 WGAN-GP [7] 损失函数的改进。我们的模型中的判别网络( F ( x ) F(x) F(x))可以看作WGAN-GP 的 “判别器” ,而变分网络和生成网络可以看作 “生成器”。 s u p F [ ⋅ ] sup_F[\cdot] supF[⋅] 和 T ( F , w ) \mathcal{T(F,w)} T(F,w) 可以看作 “WGAN” 损失术语(loss term)。 R ( F , w ) \mathcal{R}(F,w) R(F,w) 可以看作 F F F 的正则化器,也是 “-GP” (梯度惩罚,gradient penalty)术语,而 η \eta η 是梯度惩罚权重。
另外,WGAN-GP [7] 中的术语, L ~ B u z z \mathcal{\widetilde L}_{Buzz} L Buzz 也添加了从贝叶斯训练目标中借鉴的术语 K \mathcal{K} K ,为 q ϕ ( z ∣ x ) q_\phi(z|x) qϕ(z∣x) 做正则化。 λ \lambda λ 是一个可训练的变量(trainable variable),包括贝叶斯推断框架,它可以平衡 WGAN-GP 项和贝叶斯正则化。
E. Training
给定 L ~ B u z z \mathcal{\widetilde L}_{Buzz} L Buzz 是 WGAN-GP 的一种改进,所以 Buzz 的训练过程与 WGAN-GP 算法相似。生成器的参数(比如变分网络和生成网络,加上 λ \lambda λ ),记作 w w w 。而判别器的参数,(比如判别网络 F ( x ) F(x) F(x) ),记作 v v v。 R ( F , w ) \mathcal{R}(F,w) R(F,w) 在优化 w w w 时被忽略,因为它仅仅是为 F F F 而正则化, 只依赖于 v v v 。我们使用 SGVB [21] 来为 q ϕ ( z ∣ x ) q_\phi(z|x) qϕ(z∣x) 作变分推断,使用 Adam [31] 来优化神经网络参数。由于 WGAN-GP 损失具有很强的收敛性,我们的训练过程非常稳定,超参数调整很少。
将会在第4节证明,当 s → 1 s\to1 s→1 ( L B u z z \mathcal{L}_{Buzz} LBuzz 是 L ~ B u z z \mathcal{\widetilde L_{Buzz}} L Buzz 的最初似然格式), L B u z z → L v a e \mathcal{L_{Buzz}} \to \mathcal{L}_{vae} LBuzz→Lvae 。因此,我们可以在训练后,可以将模型转换到贝叶斯网络,这是第三节-F 部分需要的。因此,在算法1中,我们开始时设定 s = s 0 s=s_0 s=s0,然后通过每一个小批次设定 s ← s / 2 s\leftarrow s/2 s←s/2 逐渐减小 s s s 到 1。
F. Detection
我们需要构建 L B u z z \mathcal{L}_{Buzz} LBuzz 和 L v a e \mathcal{L}_{vae} Lvae ,即 VAE[21] 的一种特殊变体的损失函数, 如第4节中, p θ ( x ∣ z ) = 1 Z ( λ ) e x p { − λ ∣ ∣ x − G ( z ) ∣ ∣ } p_\theta(x|z)={ {1}\over{Z(\lambda)}}exp\{-\lambda || x-G(z)||\} pθ(x∣z)=Z(λ)1exp{ −λ∣∣x−G(z)∣∣}。通过这种技术,我们可以通过 算法1 将我们的模型投入到贝叶斯网络中。然后我们可以通过概率框架分离出检测输出,如下。
当检测到一个新的点时,最后一个窗口(也就是窗口中最后一个点是新的点)记作 x x x 。因为我们的目标是检测出最后一个数据点是不是异常,我们假设它是异常,然后反复使用 MCMC imputation(也在 Donut [4] 中使用),来获得重构 x ‾ \overline x x 的合理评估,步骤如下:

最后,我们把 log p θ ( x ) − log p θ ( x ‾ ) \log p_\theta(x)-\log p_\theta(\overline x) logpθ(x)−logpθ(x) 作为最后一个点的异常值评估方法,通过如下方法进行计算:
其中, z ( l ) z^{(l)} z(l)~ q ϕ ( z ∣ x ‾ ) q_\phi(z|\overline x) qϕ(z∣x), L L L 是采样数目。公式是基于评估 log p θ ( x ) − log p θ ( x ‾ ) \log p_\theta(x)-\log p_\theta(\overline x) logpθ(x)−logpθ(x) 的重要性采样 [32] 稍作修改,(记作 Buzz-strict 检测器)。在对 log p θ ( x ) \log p_\theta(x) logpθ(x) 计算重要性采样公式时,我们使用 q ϕ ( z ∣ x ‾ ) q_\phi(z|\overline x) qϕ(z∣x) 来取代 q ϕ ( z ∣ x ) q_\phi(z|x) qϕ(z∣x) 。因为 q ϕ ( z ∣ x ) q_\phi(z|x) qϕ(z∣x) 可能因为异常的影响而有所偏差。图6 中的实验结果证实了这种猜测。异常检测的异常分数阈值是如 [4] 通过最佳 F-score 进行选择的。
4. THEOREM(定理)
限于篇幅,这里不再翻译原版论文。更多翻译内容请参考我的个人博客 https://smileyan.cn/#/ad/Buzz
相关资源
这里介绍大家最关心的内容,有源代码吗?额,目前为止我还没有找到源码。
这里有关于这篇论文的 PPT,但是由于没有视频,没有原稿,其实参考价值不是很大:https://netman.aiops.org/wp-content/uploads/2019/08/infocom-chinese.pdf
其次,也不知道具体使用的是什么数据集,估计和 Donut 类似,但是 KPI 更加复杂,绘制出来的曲线也应该不是那么光滑的。
算法分析
事实上,我个人认为,读这篇论文的顺序是这样的,先大概看一下(忽略第4部分),大致清楚这个是怎么回事以后,再考虑一下要不要去看第4部分,因为第 4 部分是定理部分,相对而言,既很难看懂,也不一定能有参考价值 —— 如果不是想做这类型的论文的话。
除去第4部分相关定理和前面的背景介绍,我们概述一下这篇论文就简单很多了:
Buzz 总体结构
这一部分非常容易理解,这与 Donut 的总体结构基本上差不多。预处理(preprocessing,注:图片中有误)、训练、检测。推荐对比一下 Donut 来看差别在哪里, Donut 论文介绍。
对抗性训练与检测
这应该是这篇论文最大的亮点,总体框架是一个 WGAN ,而 WGAN 其中的生成网络是 VAE。从最简单的 GAN,由于基于 Wasserstein 距离计算,成为 WGAN,接着对于 GAN 中的生成模型下手,替换成为 VAE,因而得到了现在的模型。
对抗性训练的过程与普通的GAN类似,论文介绍是在 WGAN-GP 基础上进行了改进。但是只要是对抗生成模型就差不多是这个过程:不断优化生成模型使得生成模型生成数据尽可能接近于真实数据;不断优化判别模型使得判别模型依然能够很好地识别生成数据。
而异常检测的过程必须结合算法1而分析了。
- 初始化参数 w w w,生成模型的参数; v v v,判别模型的参数; s s s ,邻域大小; b b b,批量大小。
- repeat1
- repeat2
- 这个for循环是指判别迭代,其中的 n c r i t i c n_{critic} ncritic 是指迭代次数。
- 满足领域条件(s.t. NC) 情况下,采样 w 1 , . . . , w b w_1,...,w_b w1,...,wb。其中 b b b 是指批次大小。
- 赋值 L v \mathcal{L}_{v} Lv 与 L w \mathcal{L}_w Lw 为 0。
- 对于批次中每个数据,循环。
- 定义临时变量 L i \mathcal{L}_i Li 等。
- 对于每一个数据,进行相应的损失计算。
- 相应的损失计算。
- 相应的损失计算。
- 相应的损失计算。
- 相应的损失计算。
- 相应的损失计算。
- 相应的损失计算。
- 结束对每一个数据的循环。
- 计算本批次的总损失 L v \mathcal{L}_v Lv 。
- 计算本批次的总损失 L w \mathcal{L}_w Lw。
- 结束对每一个批次的循环。
- 如果循环下标 t 等于判别迭代次数,则优化生成模型。
- 如果循环下标 t 不等于判别迭代次数,则优化判别模型。
- 结束循环
- s ← s / 2 s\leftarrow s/2 s←s/2, b ← 2 b b\leftarrow 2b b←2b
- 当 s = 0 时,结束循环。
分区思想
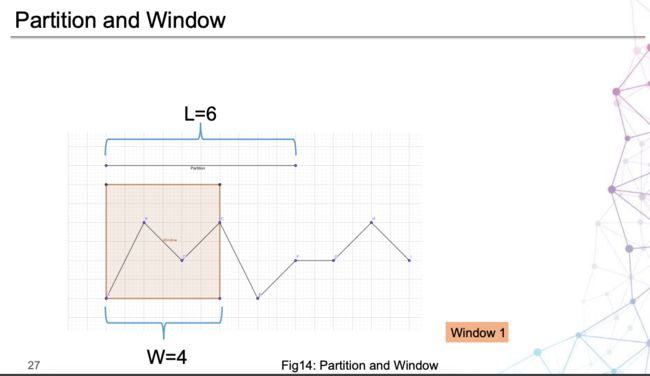
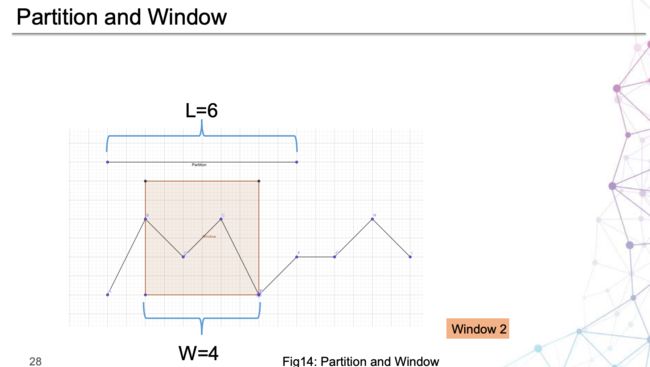
论文有一个很重要的想法:分区。结合图3,查看一下这个例子,其中一小块一小块就是指分区思想:

具体是如何分区的,请参考第3节的D部分。
总结
论文将 VAE 应用在 GAN 中,并且根据 VAE 的特点对目标函数进行了一些改进,这个过程中牵扯到不少定理与证明。但是由于时间关系,本人并没有仔细阅读这一部分,但是如果有小伙伴对这一方面感兴趣,并且遇到了一些问题,也同样欢迎留言,我一定认真阅读,想办法解决问题。
与 Donut 比起来,这篇论文强调的是:即便是对于复杂的 KPIs,Buzz 也能很好处理——而 Donut 适合于处理平滑的 KPI 数据。
另外,论文提出的分区的思想是很值得一提的,也就是说,在 Donut 中,输入模型的数据的基本单位是 窗口,并且在窗口之外没有更大的单位了:直接把 KPI 数据切分成若干个窗口。而 Buzz 是先分割成多个区域,然后再把每个区域像 Donut 一样进行切分窗口。这样的好处大概是引入了 “局部” 的概念,对于复杂 KPI 能够更好地提取特征,进行训练与检测。
感谢 您的 阅读、点赞、收藏 和 评论 ,别忘了 还可以 关注 一下哈,感谢 您的支持!
Smileyan
2021.5.4 22:02