python-XGBoost应用（回归）

以下内容笔记出自‘跟着迪哥学python数据分析与机器学习实战’，外加个人整理添加，仅供个人复习使用。

---

通过一个数据集展示XGBoost的回归建模过程，保险赔偿预测。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

from scipy import stats
import seaborn as sns
from copy import deepcopy
import warnings
warnings.filterwarnings('ignore')

1. 导入数据

train=pd.read_csv(r'train.csv')
print('训练集：\n',train.shape)
test=pd.read_csv(r'test.csv')
print('测试集：\n',test.shape)

训练集：
(188318, 132)
测试集：
(125546, 131)

#看一下数据集前20列和后20列
print('First 20 columns:\n',list(train.columns[:20]),'\n')
print('Last 20 columns:\n',list(train.columns[-20:]))

train.head(6)

可以看到，大概有116个种类属性，和14个连续属性，还有ID和最后的赔偿数据loss,共132列

1.1 数据特征查看（连续特征 or 离散特征）

train.describe()

可以看到，连续型数据已经被缩放到[0,1]区间内，均值基本为0.5。可知是实际数据经过了数据预处理，我们拿到的是特征数据。

由上面可以看到，float64型数据有15列，int64型数据有1列（应该是id列），object型数据有116列。另一种抽取方式是：

cat_features=list(train.select_dtypes(include=['object']).columns)
print('cat:{} features'.format(len(cat_features)))

cat:116 features

cont_features=list(train.select_dtypes(include=['float64','int64']).columns)
print('continuous:{} features'.format(len(cont_features)))

con_features2=[cont for cont in 
               list(train.select_dtypes(include=['float64','int64']).columns)
              if cont not in ['loss','id']]
print('continuous not include loss and id:{} faetures'.format(len(con_features2)))

continuous:16 features
continuous not include loss and id:14 faetures

id_col=list(train.select_dtypes(include=['int64']).columns)
print('A column of int64:{}'.format(id_col))

A column of int64:[‘id’]

1.2 查看缺失值

#train.isnull().sum()   #不易看出来是否有
pd.isnull(train).values.any()   #没有缺失值

1.3 查看类别变量特征（有多少类别）

train['cat1'].value_counts().shape[0]

2

cat_uniques=[]
for cat in cat_features:
    cat_uniques.append((cat,train[cat].value_counts().shape[0]))
#转换为数据框
cat_uniques=pd.DataFrame(cat_uniques)
cat_uniques.columns=['cat_name','unique_values']
print(cat_uniques.shape)
cat_uniques.head()

#作图看分布
print('二值:\n',cat_uniques[cat_uniques.unique_values==2].shape[0])
print('多值：\n',cat_uniques[cat_uniques.unique_values>2].shape[0])
plt.figure(figsize=(8,4))
plt.hist(cat_uniques.unique_values,bins=50)
plt.show()

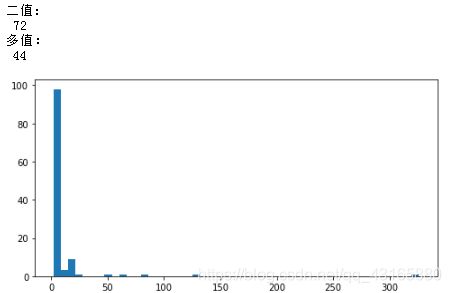
大部分特征是二值的（72/116),44个特征的类别多于2，其中一个有三百多个类别

1.4 查看因变量特征

plt.figure(figsize=(16,8))
plt.plot(train['id'],train['loss'])
plt.xlabel('id')
plt.ylabel('loss')
plt.legend()
plt.show()

（注意，这不是直方图，是分布图，是看不出峰度与偏度的）

损失值中几个显著的峰值表示严重事故。这样的数据分布，是的这个功能非常扭曲，导致回归的效果不佳。

事实上，偏度度量了实值随机变量的均值分布的不对称性。我们可以计算一下损失的偏度：

print('损失数据（因变量）偏度值：\n',
     stats.mstats.skew(train['loss']).data)
#也可以做直方图观察数据特点

损失数据（因变量）偏度值：
3.7949281496777445

• 偏度（skewness),是样本的三阶标准化矩。正态分布为0，右偏分布的偏度>0，左偏分布的偏度<0。
• 峰度（kurtosis),是样本的四阶标准化矩。正态分布为3，厚尾>3，瘦尾<3.

可知因变量数据是右偏。对数据进行对数变换，通常可以改善倾斜，可以使用np.log

print('对数化后的因变量数据偏度：\n',
     stats.mstats.skew(np.log(train['loss'])).data)

对数化后的因变量数据偏度：
0.0929738049841997

#对比下未对数化和对数化结果
plt.rcParams['font.sans-serif']='SimHei'
plt.figure(figsize=(16,5))
plt.subplot(121)
plt.hist(train['loss'],bins=50)
plt.title('损失数据（未对数化）')

plt.subplot(122)
plt.hist(np.log(train['loss']),bins=50,color='g')
plt.title('损失数据（对数化）')
plt.show()

可以看到，对数化之前的数据是右偏，对数化后基本正态分布

train['log_loss']=np.log(train['loss'])

1.5 连续变量特征

连续变量比较多，16个，一个个看不太现实，可以做的是做直方图，查看其分布情况

train[con_features2].hist(bins=60,figsize=(16,12))

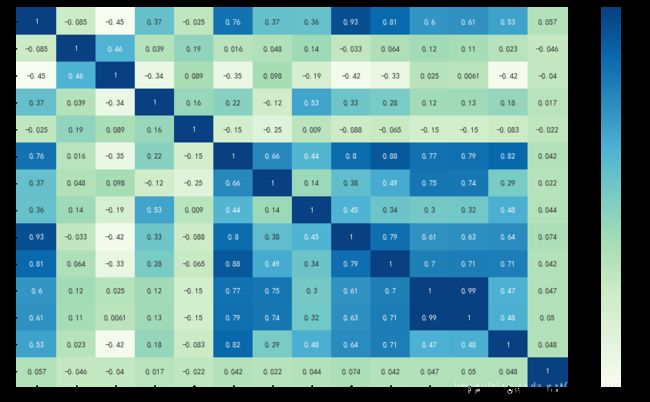
1.6连续变量的相关性

plt.figure(figsize=(16,9))
corr=train[con_features2].corr()
sns.heatmap(corr,annot=True,cmap='GnBu')

有几个特征之间有很高相关性

2. 开始建模（连续变量的预测）

import xgboost as xgb
import pickle
from sklearn.metrics import mean_absolute_error,make_scorer
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import GridSearchCV
from scipy.sparse import csr_matrix,hstack
from sklearn.model_selection import KFold,train_test_split
from xgboost import XGBRegressor

2.1 将自变量与因变量分开

ntrain=train.shape[0]

features=[x for x in train.columns 
          if x not in ['id','loss','log_loss']]
train_x=train[features]
train_y=train['log_loss']

print('Xtrain:',train_x.shape)
print('ytrain:',train_y.shape)

Xtrain: (188318, 130)
ytrain: (188318,)

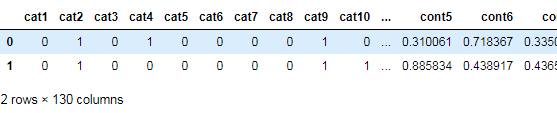
train_x[cat_features].head(6)

for c in range(len(cat_features)):
    train_x[cat_features[c]]=train_x[cat_features[c]].astype('category').cat.codes
train_x.head(2)   #将分类变量编码
#不用哑变量，用哑变量的时候是要计算距离的时候，这里是切，没用到计算距离

2.2 简单xgb模型

首先训练一个基本的xgboost模型，然后进行参数调节，通过交叉验证观察结果的变换，使用平均绝对误差来衡量

mean_absolute_error(np.exp(y),np.exp(yhat))

xgboost自定义了一个数据矩阵类DMatrix，会在训练开始时进行一遍预处理，从而提高每次迭代的效率。

xgboost参数：
- booster : gbtree
- objective : 'multi:softmax' 多分类问题
- num_class : 10,类别数，与multisoftmax并用
- gamma : 损失下降多少才进行分裂
- max_depth : 12 树深度，越大越容易过拟合
- lambda : 2 控制模型复杂度的权重值的L2正则化项参数，参数越大，模型越不容易过拟合（参数为0时，相当于没有正则化项，那么就是没限制，容易过拟合。所以参数越大，限制越大，越不易过拟合）
- subsample : 0.7，随机采集训练样本
- colsample_bytree : 0.7，生成树时进行的列采样
- min_child_weight : 3，孩子节点中最小的样本权重和。如果一个叶子节点的样本权重和小于该值则拆分过程结束。
- silent : 0，设置为1则没有运行信息输出，最好设置为0
- eta : 0.007，如同学习率 
- seed : 1000
- nthread : cpu线程数

代码：

def xg_eval_mae(yhat,dtrain):
    y=dtrain.get_label()
    return 'mae',mean_absolute_error(np.exp(y),np.exp(yhat))

dtrain=xgb.DMatrix(train_x,train['log_loss'])

xgb_params={
     
    'seed':0,
    'eta':0.1,
    'colsample_bytree':0.5,
    'silent':1,
    'subsample':0.5,
    'objective':'reg:linear',  
    'max_depth':5,
    'min_child_weight':3
}

参数解读：
https://blog.csdn.net/qq_41076797/article/details/102750544

#使用交叉验证，这里没有调节参数
bst_cvl=xgb.cv(xgb_params,dtrain,
              num_boost_round=50,  #最大迭代次数,树个数
              nfold=3,seed=0,   #表示几折
              feval=xg_eval_mae,  #以这个标准进行衡量（损失吧？）
              maximize=False,
              early_stopping_rounds=10,
               #连着10次round没有提升，迭代停止，输出最好的轮数
              verbose_eval=10, 
               #每10轮打印一次评价指标
              )  
print('CV score:',bst_cvl.iloc[-1,:]['test-mae-mean'])

得到第一个基准结果：MAE=1220.11
作图：

plt.figure()
bst_cvl[['train-mae-mean','test-mae-mean']].plot()

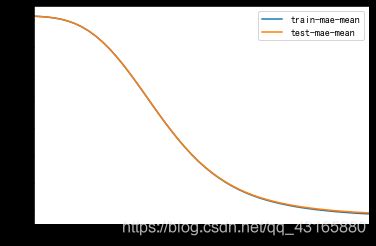
图可以看到，50个模型，每一个树模型都是建立在其前一个树模型之上的，MAE（平均绝对误差，exp）在不断降低，说明训练效果越来越好。训练集和测试集的误差都是在降低，测试集误差没有出现提高现象，说明基础模型（包含50个基础模型）没有过拟合。

2.3 进一步扩大基础模型个数

#建立100个树模型
bst_cv2=xgb.cv(xgb_params,dtrain,
              num_boost_round=100,
              nfold=3,seed=3,
              feval=xg_eval_mae,
              maximize=False,
              early_stopping_rounds=10,
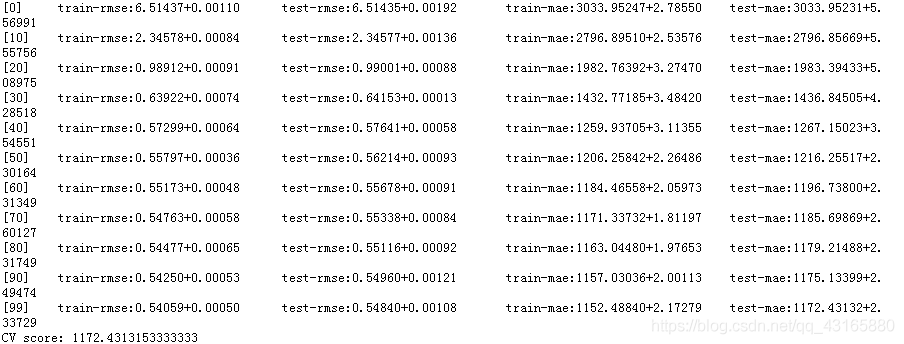
              verbose_eval=10)
print('CV score:',bst_cv2.iloc[-1,:]['test-mae-mean'])

#作图看一下是否过拟合
plt.figure(figsize=(16,4))
plt.subplot(1,2,1)
plt.plot(bst_cv2[['train-mae-mean','test-mae-mean']])
plt.legend(['training loss','test loss'])
plt.title('100 rounds of training')

plt.subplot(1,2,2)
plt.plot(bst_cv2.iloc[40:][['train-mae-mean','test-mae-mean']])
plt.legend(['training loss','test loss'])
plt.show()

有些过拟合，但不严重。

新纪录MAE=1172.43,比上一次要好。还可以改变其他参数（下次讨论…）