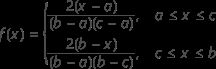参考:
https://support.minitab.com/zh-cn/minitab/18/help-and-how-to/probability-distributions-and-random-data/how-to/probability-distributions/methods-and-formulas/methods-and-formulas/
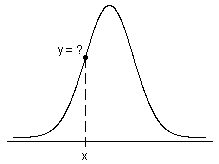
概率密度函数
随机变量 X 的概率密度函数,使您可以计算事件的概率,如下所示:
对于连续分布,X 在区间 (a, b) 中具有值的概率是其在区间 (a, b) 中的下的区域。
对于离散分布,X 在区间 (a, b) 中具有值的概率是 (a, b) 中 X 的可能离散值的(也称为概率密度函数)之和。
可使用确定随机变量 X 在已知值 x 处的概率密度函数的值
累积分布函数
累积分布函数 (CDF) 计算给定 x 值的累积概率。可使用 CDF 确定取自总体的随机观测值将小于或等于特定值的概率。还可以使用此信息来确定观测值将大于特定值或介于两个值之间的概率。
- 对于连续分布,CDF 给出概率密度函数下的区域,最多至您指定的 x 值。
- 对于离散分布,CDF 给出您指定的 x 值的累积概率。
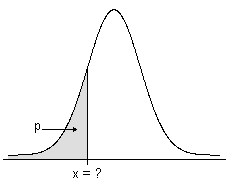
逆累积概率
对于闭区间 [0,1] 中的数字 p,随机变量 X 的累积分布函数 (ICDF) 确定(在可能的情况下)一个值 x(使 X≤x 的概率大于或等于 p)。
Beta 分布 / 贝塔分布
Beta 分布常用于表示具有自然上限和下限的过程。
| 项 | 说明 |
|---|---|
| α | 形状参数 1 |
| β | 形状参数 2 |
| Γ | Gamma 函数 |
| a | 下限 |
| b | 上限 |
https://www.cnblogs.com/coshaho/p/9658135.html
二项分布
二项分布用于表示在 n 个独立试验中发生的事件数。可能值包括从零到 n 的整数。
均值 = np
方差 = np(1 – p)
| 项 | 说明 |
|---|---|
| n | 试验数 |
| x | 事件数 |
| p | 事件概率 |
https://www.jianshu.com/p/59335680cc29
Cauchy 分布 / 柯西分布
Cauchy 分布沿零对称,但其尾部接近零的速度要比正态分布慢。
| 项 | 说明 |
|---|---|
| a | 位置参数 |
| b | 尺度参数 |
| π | Pi (~3.142) |
如果不指定值,Minitab 使用 a = 0,b = 1。
卡方分布
如果 X 具有标准正态分布,X2 具有一个自由度为 1 的卡方分布,则允许它作为一个常用采样分布。
n 个独立 X2 变量(其中 X 具有标准正态分布)的总和具有卡方分布(自由度为 n)。卡方分布的形状取决于自由度的数量。
均值 = v
方差 = 2v
| 项 | 说明 |
|---|---|
| ν | 自由度 |
| Γ | Gamma 函数 |
| e | 自然对数的基数 |
离散分布
离散分布是您自己定义的一种分布。例如,假设您想了解一个由三个值 -1、0、1 组成的分布,其概率分别是 0.2、0.5 和 0.3。如果向工作表的列中输入值,则可以使用这些列来生成随机数据或计算概率。
| 值 | 概率 |
|---|---|
| −1 | 0.2 |
| 0 | 0.5 |
| 1 | 0.3 |
指数分布
可使用指数分布对故障间的间隔时间进行建模(例如,当单元具有恒定、瞬时的故障率(风险函数))。指数分布是 Weibull 分布和 Gamma 分布的一种特殊情况。
均值 = θ + λ
方差 = θ2
| 项 | 说明 |
|---|---|
| θ | 尺度参数 |
| λ | 阈值参数 |
| exp | 自然对数的基数 |
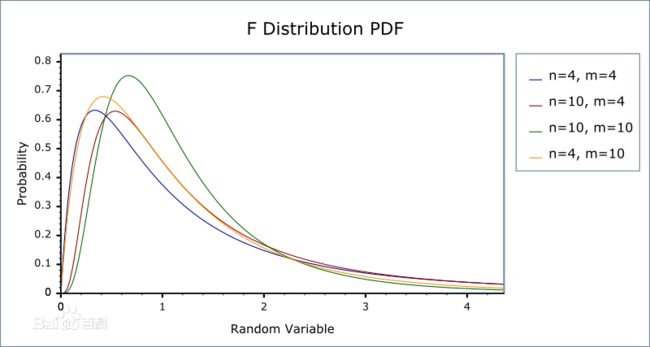
F 分布
F 分布也称为方差比值分布,具有两种类型的自由度:分子自由度和分母自由度。它是两个独立的带有卡方分布的随机变量(每个变量被其自由度所除)的比值的分布。
| 项 | 说明 |
|---|---|
| Γ | Gamma 函数 |
| u | 分子自由度 |
| v | 分母自由度 |
Gamma 分布
Gamma 分布通常用于对正向偏斜的数据建模。
均值 = ab + θ
方差 = ab2
| 项 | 说明 |
|---|---|
| a | 形状参数(当 a = 1 时,Gamma PDF 与指数分布 PDF 相同) |
| b | 尺度参数 |
| θ | 阈值参数 |
| Γ | Gamma 函数 |
| e | 自然对数的基数 |
一些参考使用 1/b 作为参数。
几何分布
离散几何分布适用于一系列独立 Bernoulli 试验(其中包含概率为 p 的相关事件)。
如果随机变量 X 是生成一个事件(具有概率 p)所需执行的试验总次数,则 X 概率质量函数 (PMF) 由下式给出:
如果随机变量 Y 是在观测的第一个事件(具有概率 p)之前发生的非事件数,则 Y 的概率质量函数 (PMF) 由下式给出:
| 项 | 说明 |
|---|---|
| X | 生成一个事件所需执行的试验数, Y + 1 |
| Y | 在第一个事件之前发生的非事件数 |
| p | 事件在每个试验中的发生概率 |
超几何分布
在不进行替换的情况下,超几何分布可用于从较小的总体中提取的样本。例如,您有 N 台电视机,其中 N1 是优良品(成功),N2 是缺陷品(失败)。如果从 N 中随机采样 n 台电视机(不进行替换),您可以发现在 n 台电视机中概率 x 即为良好状态。
| 项 | 说明 |
|---|---|
| N | N1 + N2 = 总体大小 |
| N1 | 总体中的事件数 |
| N2 | 总体中的非事件数 |
| n | 样本数量 |
| x | 样本中的事件数 |
整数分布
整数分布是一组整数上的离散均匀分布。每个整数具有相同的出现概率。
正态分布
正态分布(也称为高斯分布)是最常使用的统计分布,因为此分布可对许多物理、生物和社会过程进行建模。
累积分布函数 (CDF) 是:
均值 = μ
方差 = σ 2
标准差 = σ
| 项 | 说明 |
|---|---|
| exp | 自然对数的基数 |
| π | Pi (~3.142) |
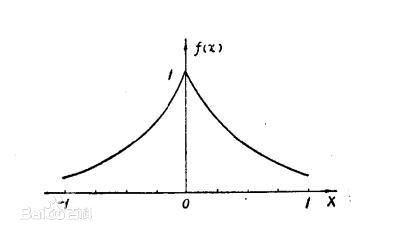
Laplace 分布 / 拉普拉斯分布
当与正态分布相比,分布的波峰更为尖锐时,将使用 Laplace 分布。
均值 = a
方差 = 2b2
| 项 | 说明 |
|---|---|
| a | 位置参数 |
| b | 尺度参数 |
| e | 自然对数的基数 |
最大极值分布
可使用最大极值分布对分布中的最大值进行建模。如果您具有一系列指数分布,并且 X(n) 是第 n 个分布中的最大值,则 X(n) – ln(n) 在分布中收敛于最大极值分布。因此,对于很大的 n 值,最大极值分布是 X(n) – ln(n) 的分布的充分近似。
累积分布函数 (CDF) 是:
均值 = μ + γσ
方差 = π 2 σ 2 / 6
| 项 | 说明 |
|---|---|
| σ | 尺度参数 |
| μ | 位置参数 |
| γ | Euler 常数 (~0.57722) |
Logistic 分布
一种对称的连续分布,与正态分布类似,但尾部更厚。
累积分布函数 (CDF) 是:
均值 = μ
| 项 | 说明 |
|---|---|
| μ | 位置参数 |
| σ | 尺度参数 |
对数 Logistic 分布
如果 Y = log (x – λ) 具有 logistic 分布,则变量 x 具有对数 Logistic 分布(阈值为 λ)。
累积分布函数 (CDF) 是:
| 项 | 说明 |
|---|---|
| μ | 位置参数 |
| σ | 尺度参数 |
| λ | 阈值参数 |
| Γ | Gamma 函数 |
| exp | 自然对数的基数 |
对数正态分布
如果 log(x – λ) 具有正态分布,则变量 x 具有对数正态分布。
累积分布函数 (CDF) 是:
| 项 | 说明 |
|---|---|
| μ | 位置参数 |
| σ | 尺度参数 |
| λ | 阈值参数 |
| π | Pi (~3.142) |
负二项分布
离散负二项分布适用于一系列独立 Bernoulli 试验(其中包含概率为 p 的事件)。
Poisson 分布 / 泊松分布
Poisson 分布是可对基于恒定发生率的事件数量建模的离散分布。当独立试验数量大并且成功概率小时,Poisson 分布可用作二项式的近似。
均值 = λ
方差 = λ
| 项 | 说明 |
|---|---|
| e | 自然对数的基数 |
最小极值分布
可使用最小极值分布对分布中的最小值进行建模。如果 Y 服从 Weibull 分布,则 log(Y) 服从最小极值分布。
累积分布函数 (CDF) 是:
| 项 | 说明 |
|---|---|
| ξ | 位置参数 |
| θ | 尺度参数 |
| e | 自然对数的基数 |
| v | Euler 常数 (~0.57722) |
t 分布
随着自由度增加,t 分布收敛到正态分布。t 分布可用于执行以下操作:
- 创建正态分布中的总体均值的置信区间(当方差未知时)。
- 确定正态总体中的两个样本均值(具有未知但相等的方差)是否显著不同。
-
检验回归系数的显著性。
均值 = 0(当 ν > 0 时)

| 项 | 说明 |
|---|---|
| Γ | Gamma 函数 |
| v | 自由度 |
| π | Pi (~3.142) |
三角分布
三角分布的 PDF 具有一个三角形状。
| 项 | 说明 |
|---|---|
| a | 下端点 |
| b | 上端点 |
| c | 模式(PDF 尖峰所在的位置) |
均匀分布
均匀分布的特征是数据在一个区间中均匀地分布,最小值为 a,最大值为 b。
| 项 | 说明 |
|---|---|
| a | 下端点 |
| b | 上端点 |
Weibull 分布 / 韦布尔分布
Weibull 分布可对产品失效时间进行建模。
累积分布函数 (CDF) 是:
| 项 | 说明 |
|---|---|
| α | 尺度参数 |
| β | 形状参数,当 β = 1 时,Weibull PDF 与指数分布 PDF 相同 |
| λ | 阈值参数 |
| Γ | Gamma 函数 |
| exp | 自然对数的基数 |
一些参考使用 1/α 作为参数。