欧拉角和四元数
笔记主要摘自下列博文和回答中
如何通俗地解释欧拉角?之后为何要引入四元数? - 知乎
【Unity编程】四元数(Quaternion)与欧拉角 - Andrew的游戏世界 - CSDN博客
【Unity编程】欧拉角与万向节死锁(图文版) - Andrew的游戏世界 - CSDN博客
欧拉角
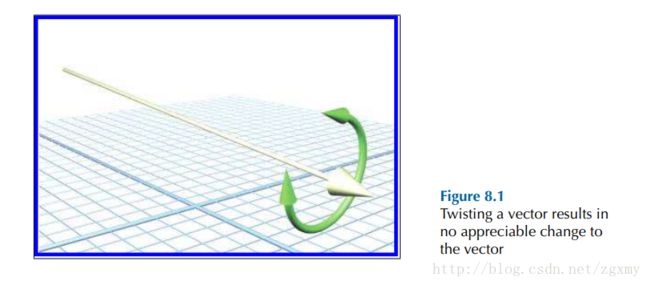
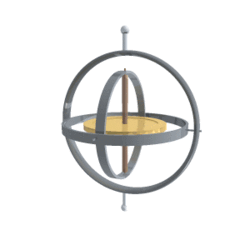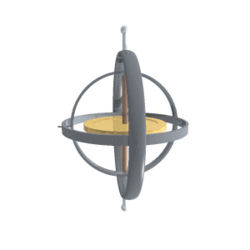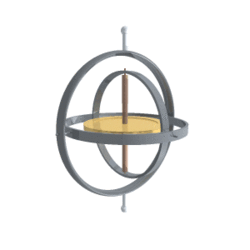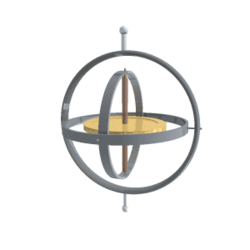
欧拉角:由三个角度组成,在特定坐标系下用于描述刚体的orientation。orientation可以理解为形态,用来唯一地确定定点转动明体位置的三个一组独立角参量,它不是一个方向或向量,如图1的向量,无论怎么旋转它都是不会改变的,因为它没有orientation。
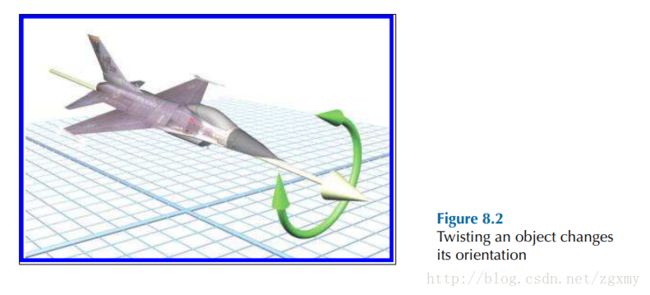
而在图2中当你旋转物体时,它的orientation就会发生改变。描述一个向量用两个维度就可以(忽略长度信息),而描述orientation至少需要三个角度,即欧拉角,总结起来,欧拉角就是用来表示三维坐标系中方向和方向变换的。
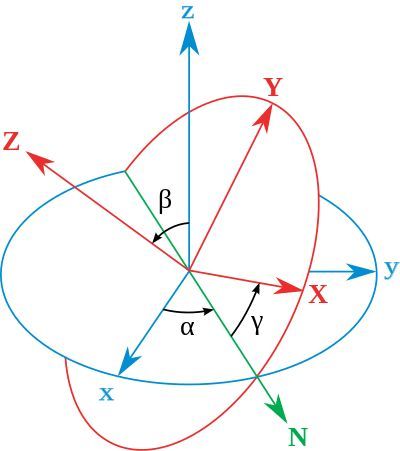
下面这个图解释了如何通过欧拉角进行旋转
图中有两组坐标,一组是xyz,它是全局坐标保持不懂,而XYZ则是局部坐标,跟着物体一起旋转。旋转步骤为:1.绕着全局z轴转了角;2.绕着自己的X轴转了角;3.绕这自己的Z轴转了角。下面的图4更加清晰地展示了旋转的过程 (对应, 对应, 对应 )
我们把上面的旋转顺序记为zXZ(习惯称为zxz顺规),加上对应的角度就构成了一个完整的欧拉角,表示为 zXZ—(,,)
万向节
维基百科中关于平衡环架的一段描述
平衡环架(英语:Gimbal)为一具有枢纽的装置,使得一物体能以单一轴旋转。由彼此垂直的枢纽轴所组成的一组三只平衡环架,则可使架在最内的环架的物体维持旋转轴不变,而应用在船上的陀螺仪、罗盘、饮料杯架等用途上,而不受船体因波浪上下震动、船身转向的影响。
它的样子如图5所示
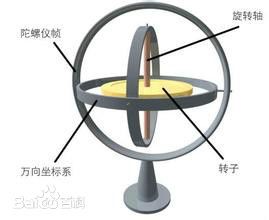
其组成如下图所示
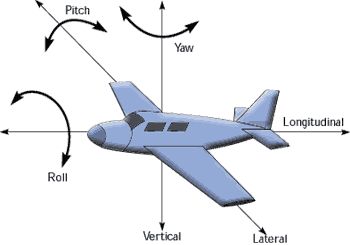
万向节与欧拉角的工作方式类似,三层嵌套的圆环,它们互相交叉,带来了三个方向自由度的旋转。如图6所示,沿着机身右方轴(Unity中的+X)进行旋转,称为pitch,中文叫俯仰。 沿着机头上方轴(Unity中的+Y)进行旋转,称为Yaw,中文叫偏航。 沿着机头前方轴(Unity中的+Z)进行旋转,称为Roll,中文叫桶滚。
万向节死锁
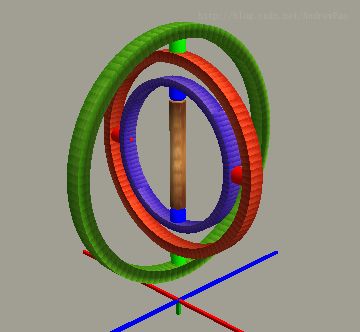
了解了上面一些东西后,我们来了解万向节死锁产生和问题,为了解释清楚问题,这里有一个简单的陀螺仪示意图。
把三个Gimbal环用不同的颜色做了标记,底部三个轴向,RGB分别对应XYZ。 假设现在这个陀螺仪被放在一艘船上,船头的方向沿着+Z轴,也就是右前方。通过博文中的演示可知道当船体分别发生俯仰,偏航和桶滚时,平衡环架中的转子和平衡轴都能通过自身的调节保持平衡的状态,而使移动只发生在陀螺仪内部的相对移动。
这样看似在任何摇晃下这个简陋的陀螺仪都能通过自身的调整使其保持稳定的平衡,但是在我们假设船体发生了事故,船首扬起了90°(即俯仰旋转),此时陀螺仪会呈现图9这种状态(红色圆环俯仰转动90°成竖直状态)
此时,船体再次发生转动,沿着当前世界坐标的+Z轴(蓝色轴,应该正指向船底)进行转动会发生什么情况呢,如图10所示
这中现象为什么会出现呢?
之前陀螺仪之所以能通过自身调节,保持平衡,是因为存在可以相对旋转的连接头。在这种情况下,已经不存在可以相对旋转的连接头了。那么连接头呢?去了哪里?显然,它还是在那里,只不过是,连接头可以旋转的相对方向不是现在需要的按着+Z轴方向。从上图中,我们清楚地看到:
红色连接头:可以给予一个相对俯仰的自由度。
绿色连接头:可以给予一个相对偏航的自由度。
蓝色连接头:可以给予一个相对偏航的自由度。
三个连接头提供的自由度只对应了俯仰和偏航两个自由度,桶滚自由度丢失了。这就是陀螺仪上的“万向节死锁”问题。
而万向节的死锁也是欧拉角在应用时的一大缺点,为解决这个问题,可以引入四元数来对旋转变换进行描述。
四元数
欧拉旋转定理
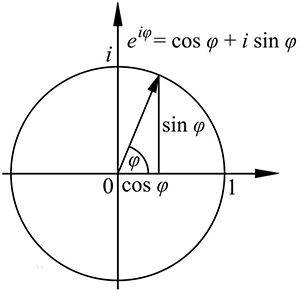
由下图可以看出,当长度为1时,矢量落在长度为1的圆形上,此时实数轴上的a = cos(φ),虚数轴上的b = sin(φ),其中φ为旋转角度。此时的表示形式为 e = cos(φ) + sin(φ)i
当圆上的一个矢量进行了连续的旋转时时,假设先旋转φ,再旋转θ,则结果应该是两个旋转的角的和的复数形式,即 e = cos(φ+θ)+sin(φ+θ)i。假设:e1= cos(φ) + sin(φ)i (表示旋转了φ角度),e2= cos(θ) + sin(θ)i (表示旋转了θ角度),根据公式演算可得e和e1、e2的关系为 e = e1*e2,也就是说,连续的旋转(例如这里旋转φ再旋转θ),可以使用两个复数的乘积进行表示,这就是欧拉定理和复数结合的作用,它能够方便的表示出二维矢量的旋转变化。
四元数定义
四元数的定义一般是 q=w+xi+yj+zk,其中 w,x,y,z是实数。同时,有:
i*i=-1; j*j=-1;k*k=-1,四元数也可以表示为: q=[w,v]
其中v = (x,y,z)是矢量,w是标量,虽然v是矢量,但不能简单的理解为3维空间的矢量,它是4维空间中的的矢量,这点比较抽象,不做深究。
通俗的讲,一个四元数描述了一个旋转轴和一个旋转角度。当然也可以随意指定一个角度一个旋转轴来构造一个四元数。这个角度是相对于单位四元数而言的,也可以说是相对于物体的初始方向而言的。
有多种方式可表示旋转,如 axis/angle、欧拉角(Euler angles)、矩阵(matrix)、四元组等。 相对于其它方法,四元数有其本身的优点:
1.四元数不会有欧拉角存在的万向节死锁问题
2.四元数由4个数组成,旋转矩阵需要9个数
3.两个四元数之间更容易插值
4.四元数、矩阵在多次运算后会积攒误差,需要分别对其做规范化(normalize)和正交化(orthogonalize),对四元数规范化更容易
与旋转矩阵类似,两个四元组相乘可表示两次旋转
四元数——对旋转角表示方法
这里主要参考了【Unity技巧】四元数(Quaternion)和旋转 - candycat - CSDN博客的文章做了一个我本人学习的总结。
我们下面使用q = ((x, y, z),w) = (v, w),其中v是向量,w是实数,这样的式子来表示一个四元数。我们可以使用一个四元数q=((x,y,z)sinθ2,cosθ2) 来执行一个旋转。具体来说,如果我们想要把空间的一个点P绕着单位向量轴u = (x, y, z)表示的旋转轴旋转θ角度,我们首先把点P扩展到四元数空间,即四元数p = (P, 0)。那么,旋转后新的点对应的四元数(计算得的四元数的实部为0,虚部系数就是新的坐标)为: p′=qpq−1
其中,q=(cosθ2, (x,y,z)sinθ2) ,q−1=q∗N(q),由于u是单位向量,因此N(q)=1,即q−1=q*。
右边表达式包含了四元数乘法。相关的定义如下:(其中v,v1,v2为向量)
四元数乘法:q1q2=(v1×v2+w1v2+w2v1,w1w2−v1⋅v2)
共轭四元数:q*=(−v,w)
四元数的模:N(q) = √(x^2 + y^2 + z^2 +w^2),即四元数到原点的距离
四元数的逆:q^-1=q∗N(q)
关于四元数各种性质的分析可参考下面这个链接中的内容
【Unity编程】四元数(Quaternion)与欧拉角 - Andrew的游戏世界 - CSDN博客
由于我所需要的是结果和能够使用结果,所以不列出证明,其主要思想是构建了一个辅助向量k,它是将p绕旋转轴旋转θ/2得到的。证明过程尝试证明wk∗=kv∗,以此证明w与v、k在同一平面内,且与v夹角为θ。
举一个例子,把点P(1, 0, 1)绕旋转轴u = (0, 1, 0)旋转90°,求旋转后的顶点坐标。首先将P扩充到四元数,即p = (P, 0)。而q = (u*sin45°, cos45°)。求p′=qpq−1的值。最后的结果p` = ((1, 0, -1), 0),即旋转后的顶点位置是(1, 0, -1)。
如果想要得到复合旋转,只需类似复合矩阵那样左乘新的四元数,再进行运算即可。
我们来总结下四元数旋转的几个需要注意的地方:
1.用于旋转的四元数,每个分量的范围都在(-1,1);
2.每一次旋转实际上需要两个四元数的参与,即q和q*;
3.所有用于旋转的四元数都是单位四元数,即它们的模是1;
Unity中的四元数使用
实际上,在Unity里即便不知道上述公式和变换也丝毫不妨碍我们使用四元数,但是有一点要提醒你,除非你对四元数非常了解,那么不要直接对它们进行赋值。在Unity里找到对应的函数来进行四元数变换,那么可以使用这两个函数:Quaternion.Euler和Quaternion.eulerAngles。它们基本可以满足绝大多数的四元数旋转变换。
四元数和欧拉角的转换
给定一个欧拉旋转(X, Y, Z)(即分别绕x轴、y轴和z轴旋转X、Y、Z度),则对应的四元数为:
x = sin(Y/2)sin(Z/2)cos(X/2)+cos(Y/2)cos(Z/2)sin(X/2)
y = sin(Y/2)cos(Z/2)cos(X/2)+cos(Y/2)sin(Z/2)sin(X/2)
z = cos(Y/2)sin(Z/2)cos(X/2)-sin(Y/2)cos(Z/2)sin(X/2)
w = cos(Y/2)cos(Z/2)cos(X/2)-sin(Y/2)sin(Z/2)sin(X/2)
四元数 q = ((x, y, z), w)。
使用四元数解决万向节锁
一般情况下对于给定的按照一定顺规的欧拉角,将其转换成为四元数再转换为旋转矩阵进行计算,即每一个欧拉角都生成一个新的四元数和新的旋转矩阵,在使用欧拉角时这样做是没有问题的,但是在使用四元数的时候就会出现问题,因为每次输入的绕轴旋转有多个轴和多个角度,对于多次旋转绕多轴没有考虑坐标系的变化,解决办法是分别计算用户每一次输入的旋转变换矩阵,将每一次的单独的旋转变换矩阵点乘原来的旋转变换矩阵,得到最新的变换矩阵。后续的每一次变换都在这个矩阵的基础上不断的乘,也就是说每一次都是在原来的基础上再加一点点变化。
并且用四元数生成旋转矩阵相乘,运算的顺序对结果不会有影响。