2.1 基本概念与抽象数据类型
2.1.1 基本概念
线性表简称为表,是零个或多个元素(表目)的有穷序列。通常表示为:
L=(k0, k1, ..., kn-1)
线性表的逻辑结构可以用二元组L=
2.1.2 抽象数据类型
线性表的抽象数据类型如下:
ADT List is
Operations
// 创建并返回一个空线性表
List createNullList(void)
// 插入元素
int insertPre(List list, position p, DataType x)
// 插入元素
int insertPost(List list, position p, DataType x)
// 删除元素
int deleteV(List list, DataType x)
// 删除元素
int deleteP(List list, position p)
// 查找位置
position locate(List list, DataType x)
// 判断是否为空
int isNull(List list)
end ADT List
2.2 顺序表示
2.2.1 存储结构
在顺序表中,假设每个元素占用c个存储单元,则下标为i+1的元素存储位置与下标为i的元素存储位置之间,满足下列关系:
loc(ki+1) = loc(ki) + c
通常把顺序表k0的存储位置loc(k0),称为线性表的首地址或基地址,下标为i的元素ki的存储位置为:
loc(ki) = loc(k0) + i * c
定义如下:
struct SeqList {
int MAXNUM; // 顺序表中最大元素的个数
int n; // 存放线性表中元素的个数
DataType *element; // 存放线性表中的元素
};
2.2.2 运算的实现
创建空的顺序表
SeqList* createNullList_seq(int n) {
SeqList *pList = (SeqList *)malloc(sizeof(struct SeqList));
if (pList != NULL) {
pList->element = (DataType *) malloc(sizeof(DataType * n));
if (pList->element) {
pList->MAXNUM = n;
pList->n = 0;
return pList;
} else {
free pList;
}
}
return NULL;
}
判断顺序表是否为空
int isNullList_seq(SeqList *pList) {
return (pList->n == 0);
}
求顺序表的位置
int locate_seq(SeqList *pList, DataType x) {
int q;
for(q = 0; q < pList->n; q++) {
if (pList->element[q] == x) {
return q;
}
}
return -1;
}
顺序表的插入
int insertPre_seq(SeqList *pList, int p, DataType x) {
int q;
if (pList->n >= pList->MAXNUM) {
printf("Overflow!\n");
return 0;
}
if (isNullList_seq(pList)) {
pList->element[0] = x;
pList->n = 1;
return 1;
}
if (p < 0 || p > pList->n-1) {
printf("Not exit!\n");
return 0;
}
for(q = pList->n-1; q >= p; q--) {
pList->element[q+1] = pList->element[q];
}
pList->element[p] = x;
pList->n = pList->n+1;
return 1;
}
顺序表的删除
int deleteP_seq(SeqList *pList, int p) {
int q;
if (p < 0 || p > pList->n-1) {
printf("Not exit!\n");
return 0;
}
for(q = p; q < pList->n-1; q++) {
pList->element[q] = pList->element[q+1];
}
pList->n = pList->n - 1;
return 1;
}
2.2.3 分析与评价
在有n个元素的线性表里,在下标为i(第i + 1个)的元素之前插入一个元素,需要移动n-i个元素,删除下标为i(第i+1个)的元素需要移动n-i-1个元素。
插入的平均移动数是:
Mi = ∑(n -i)Pi, i=0 ~ n
删除的平均移动数是:
Md = ∑(n - i - 1) Pi', i = 0 ~ n-1
可以求得
Mi = n/2,Md = (n - 2) / 2
故插入和删除的时间代价为O(n)
2.2.4 顺序表空间的扩展
申请一个比较大的数组,用新数组代替原来的数组,先把原来数组中所有元素复制到新数组的前面,然后继续插入
扩建的代码如下:
pos1 = (DataType *) malloc(sizeof(DataType) * pList->MAXNUM * 2);
if (pos1 == null) {
return 0;
}
for(q = 0; q < pList->MAXNUM; q++) {
pos1[q] = pList->element[q];
}
free(pList->element);
pList->element = pos1;
pList->MAXNUM *= 2;
2.3 链接表示
2.3.1 单链表表示
单链表的类型如下:
typedef struct Node {
DataType info;
struct Node* link;
} Node;
typedef Node* LinkList;
2.3.2 单链表上运算的实现
创建空链表
LinkList createNullList_link(void) {
LinkList list = (LinkList) malloc(sizeof(struct Node));
if (list != NULL) {
list->link = NULL;
}
return list;
}
判断单链表是否为空
int isNullList_link(LinkList list) {
return (list->link == NULL);
}
在单链表中求得某元素的存储位置
Node * locate_link(LinkList list, DataType x) {
Node *p;
if (list == NULL) {
return NULL;
}
p = list->link;
while (p != NULL && p->info != x) {
p = p->link;
}
return p;
}
单链表的插入
int insertPost_link(LinkList list, Node *p, DataType x) {
Node *q = (Node *) malloc(sizeof(Node));
if (q == NULL) {
printf("Out of space!\n");
return 0;
} else {
q->info = x;
q->link = p->link;
p->link = q;
return 1;
}
}
在单链表中求p所指结点的前驱结点
Node *locatePre_link(LinkList list, Node *p) {
Node *p1;
if (list == NULL) {
return NULL;
}
p1 = list;
while (p1 != NULL && p1->link != p) {
p1 = p1->link;
}
return p1;
}
单链表的删除
int deleteV_link(LinkList list, DataType x) {
Node *p, *q;
p = list;
if (p == NULL) {
return 0;
}
while (p->link != NULL && p->link->info != x) {
p = p->link;
}
if (p->link == NULL) {
return 0;
} else {
q = p->link;
p->link = q->link;
free(q);
return 1;
}
}
2.3.3 分析与比较
单链表的查找、插入、删除操作的时间复杂度为 O(n)
2.3.4 单链表的改进与扩充
循环链表
单链表的最后一个结点的指针指向头结点就得到循环链表。循环链表没有增加新的存储空间,但从循环链表中任一结点出发,都能访问所有结点。
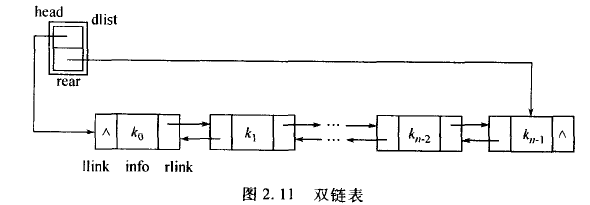
双链表
双链表在单链表的基础上,增加一个指向前驱结点的指针。定义如下:
typedef struct DoubleNode {
DataType info;
struct DoubleNode *llink, rlink;
} Double Node;
双链表结构如下所示:
循环双链表
循环双链表是在双链表的基础上将头结点和尾结点连起来。
2.4 应用举例
2.4.1 Josphus问题
2.4.2 采用顺序表模拟
2.4.3 采用循环链表模拟
2.5 矩阵
2.5.1 矩阵的顺序表示
采用顺序存储方式表示矩阵,一般有行优先顺序和列优先顺序两种
行优先顺序即元素按行向量顺序排列,第i+1个行向量紧接在第i个行向量后面。矩阵的元素排列顺序如下:
a0 0, a0 1, ..., a0 n-1, a1 0, a1 1, ..., a1 n-1, ..., am-1 0, am-1 1, ..., am-1 n-1
列优先顺序即元素按向量顺序排列,第j+1个列向量紧接在第i个列向量后面。
按行优先顺序存储,地址计算公式如下:
loc(aij) = loc(a00) + i x n + j
按列优先顺序存储,地址计算公式如下:
loc(aij) = loc(a00) + j x m + i
2.5.2 稀疏矩阵的表示方法
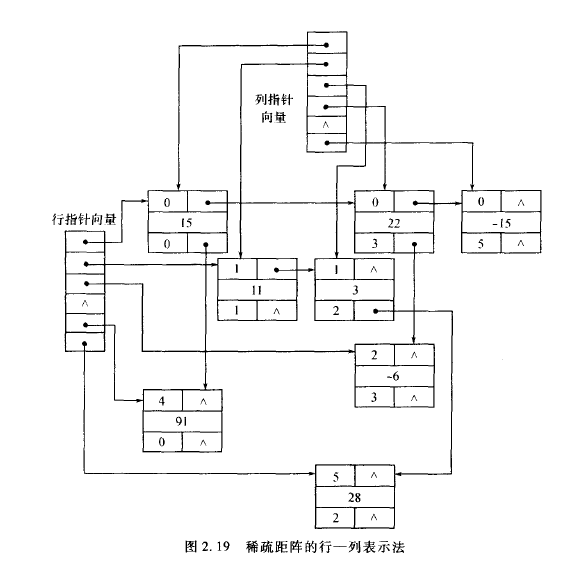
设mxn的矩阵A中有k个非零元素,又设k大大小于mxn(记为k< 用一个数组(顺序数据结构)来表示稀疏矩阵。这个数组中只存放稀疏矩阵的非零元素。每个结点包含3个字段,分别为该非零元素的行下标、列下标和值。结点间按行优先顺序排列 元素的伪地址就是在矩阵里按行优先顺序的相对位置(包括零元素一起算)。 这个方法是三元组表示法的一个变种。在三元组表示法中,结点的行下标字段是按递增顺序排列的,列下标没有规律,因此可以考虑去掉行下标字段,而加上一个有m+1个元素的辅助行向量NRA,定义如下: 广义表是线性表的推广,具有广泛的应用价值。它是表处理语言的基础结构,也可以用于表示动态存储空间的整体模型。 广义表也是零个或多个元素组成的序列。但与线性表不同,广义表中的元素允许以不同形式出现:它可以是一个院子(逻辑上不能再分解的元素),也可以又是一个广义表。作为广义表元素的广义表称为广义表的子(广义)表。一个广义表还允许直接或间接地作为它自身的子(广义)表。 但要注意的是: E1不是空广义表,它有一个空广义表作为唯一的元素,所以长度为1 每个结点由三个字段组成: 单链表示法主要的缺点是:如果要删除广义表(或子广义表)中某一元素,则需要搜索广义表中所有结点后才能进行。 原则上说,单链表中的元素个数是任意的,允许自由变化的。习惯上把这种使用期间可自由插入和删除的数据结构称为动态数据结构。在程序运行过程中,对于动态数据结构结点的分配和回收需要采用动态存储管理的方法。 当所有结点都是等长时,管理方法比较简单。 在实际应用中,往往要用到多个链表,而这些链表中的结点长度可能各不相同。这种情况下,一个简便的处理方法是,在动态区中建立多个可利用空间表,每个可利用空间表对应一种固定长度的结点。缺点是,难以真正解决多个可利用空间表的共享问题。系统开销也比较大。 为了分配一个大小为N的结点,必须检索可利用空间表中的结点,找出一个size的值大于等于N的可利用块进行分配,同时把多余部分留在可利用空间表中;如果可利用空间表中不存在这样的结点则不能分配,称之为分配失败。常用的查找方法有三种: 从上面的讨论可以看出,系统的动态去主要由两部分构成:一部分是已利用空间构成的广义表,它可能被许多程序共享,每个程序可能同时使用多个不同方式定义的链表;另一部分是可利用空间构成的广义表,它可能包含多个大小不同的可利用空间表,也可能包含多个不等长结点的可利用空间表。 碎片与废料不同,它出现在可利用空间中,但因为太小了,长期无法分配使用。虽然在动态分配和回收过程中,系统采用各种方法来减少碎片的产生,但都难以杜绝碎片的出现。为了从根本上解决碎片问题,可以采用存储压缩的方法。三元组表示法
伪地址表示法
带辅助行向量的二元组表示法
NRA[0] = 0;
NRA[i] = NRA[i - 1] + 矩阵第 i-1行中非零元素的个数(i > 0)行-列表示法
2.6 广义表与动态存储管理
2.6.1 广义表
一个广义表中所包含的元素的个数,称为这个广义表的长度。长度为零的广义表称为空(广义)表。
为了区分广义表和原子,可以用圆括号把一个广义表括起来,再用逗号来分隔广义表中的元素。一个广义表的深度,就是指广义表中所含括号的层数。
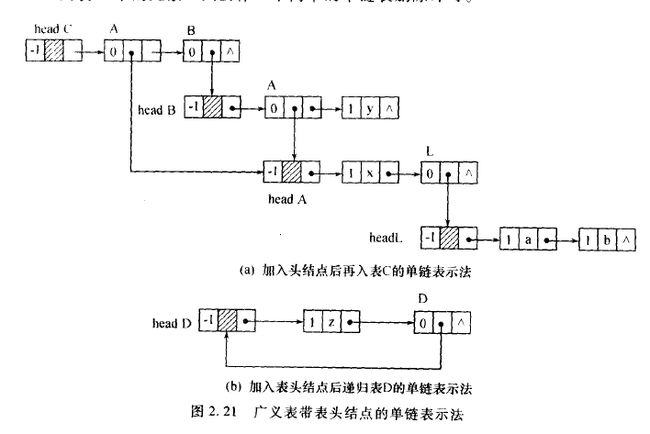
例如:E=()
L=(a, b)
A=(x, L) = (x, (a,b))
B=(A, y) = ((x, (a, b)), y)
C=(A, B) = ((x, (a, b)), ((x, (a, b)), y))
D=(z, D) =(z, (z, (z, ...)))
E1 = (E) = (())
线性表:广义表中的元素全部都是原子
纯表:广义表中的元素允许有子广义表,但所有各层子广义表均无共享
再入表:在各层子广义表中允许共享的广义表
递归表:允许广义表直接地作为自己的子广义表单链表示法
| atom | info | link |
其中atom是标志位:atom = 0 表示本结点为子广义表,这时字段info存放本原子的信息(当信息量较大是,也可以存放本原子信息存放的地址)。字段link存放于本元素同层的下一个元素所对应结点的地址,当本元素是所在层的最后一个元素时,link = NULL。
如下图所示:
带头结点的单链表示法
2.6.2 结点的动态分配与回收
等长结点的分配与回收
在系统运行初期,可以把整个可供链表动态分配的所有空间(称为动态区),按结点node类型的大小链接起来,构成一个单链表尘给可利用空间包(avail)。它与一般的链表差别在于:它是动态存储管理系统中,用于管理和记录可以分配的结点空间的单链表,不是应用程序中定义的单链表,不包括任何用户定义的信息,链接的顺序也无关紧要。当需要向某一个单链表插图一个结点时,可先从avail表中删除一个结点,然后把这个结点的空间提供给新插入结点使用;反过来,当从某个单链表中删除一个结点时,只要将这个结点从单链表中删除,然后送回到avail表中即可。不等长结点的分配与回收
另一种处理不等长结点的办法是:组织一个可以管理各种大小结点的可利用空间表。这种处理方法的优点是可以解决存储空间的共享问题,缺点是分配和回收的算法复杂了。另外,在系统长期动态运行过程中,这种方法有可能使整个空间被分割成许多大小不等的碎块,而某些碎块由于太小而长期得不到使用,则就产生了碎片问题。动态分配
2.6.3 废料收集与存储压缩
废料收集
在动态区中,还可能在一些被无用结点占用的空间,简称为无用结点(也称为废料)。
废料收集需要解决的问题是:从整个动态区的已利用空间中,找出哪些结点是无用结点,并且把它们送入可利用空间表中。存储压缩
压缩存储就是把有用的结点压缩到动态区的一端,把可利用的结点(包括碎片)压缩到动态区的另一端,使全部可利用的空间连成一片,构成一个大的可利用块。