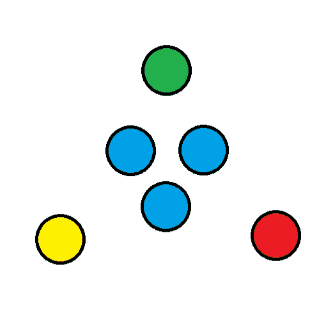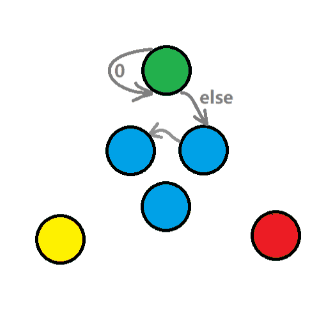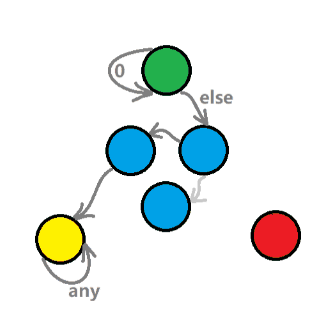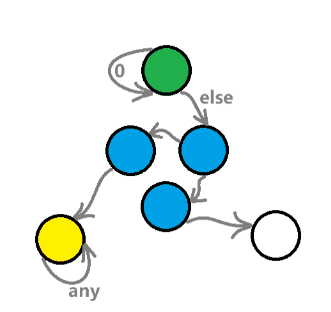夜深人静写算法(二十九)- 数位DP
文章目录
- 一、前言
- 二、数位 DP 简介
-
- 1、数位 DP 定义
- 2、数位 DP 引例
- 3、状态分析
- 三、数位 DP 代码实现
-
- 1、状态初始化
- 2、数位初始化
- 3、记忆化搜索
- 四、数位 DP 进阶
-
- 1、非法状态
- 2、饱和状态
- 3、组合状态
- 4、前导零状态
- 5、位压缩状态
- 6、二分优化
- 五、数位 DP 总结
-
- 1、状态转移图
- 2、数位 DP 模板
- 六、数位 DP 相关题集整理
一、前言
数位 DP 又称 数位动态规划,在 LeetCode 上属于难题,而 ACM 竞赛中属于中等题,甚至可以说是模板题。
数位 DP 的状态设计千变万化,但万变不离其宗,只要确定这个题是用数位 DP 求解,基本就很容易把状态套出来。当然,对于刚接触动态规划的同学,建议先看下 背包问题、最长单调子序列、最长公共子序列、记忆化搜索 等基础内容,对状态机和状态转移有一个初步的认识,那么,在学习数位 DP 时能够起到事半功倍的效果。
二、数位 DP 简介
1、数位 DP 定义
- 数位 DP 又称 数位动态规划,一般可以从题干就能确定这个题是否可以用 数位 DP 来求解。因为 数位 DP 的题目一般都描述成如下两种问法之一:
【问法1】给定一个闭区间 [ l , r ] [l, r] [l,r],求在这个区间中,满足 某些条件 的数的个数。
【问法2】如果一个数字满足 某些条件,则称之为 X X X 数,给定闭区间 [ l , r ] [l, r] [l,r],求这个区间中 X X X 数的个数。
- 这里的 某些条件 决定了状态转移的决策,这样说或许比较抽象,那么接下来,我们通过一个简单的例题来了解下 数位DP 的一般求解过程。
2、数位 DP 引例
【例题1】如果一个数的所有位数加起来是 10 10 10 的倍数, 则称之为 g o o d n u m b e r good \ number good number,求区间 [ l , r ] ( 0 ≤ l ≤ r ≤ 1 0 18 ) [l, r](0 \le l \le r \le 10^{18}) [l,r](0≤l≤r≤1018) 内 g o o d n u m b e r good \ number good number 的个数;
- 对于这个问题,朴素算法就是枚举区间里的每个数,并且判断可行性,时间复杂度为 o ( ( r − l ) c ) o((r-l)c) o((r−l)c), c = 19 c=19 c=19,肯定是无法接受的。
1)差分转换
- 对于区间 [ l , r ] [l, r] [l,r] 内求满足数量的数,可以利用差分法分解问题;
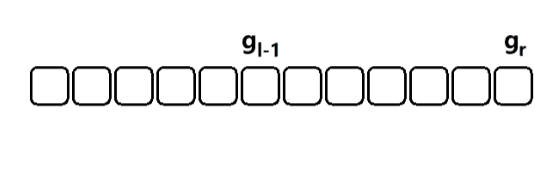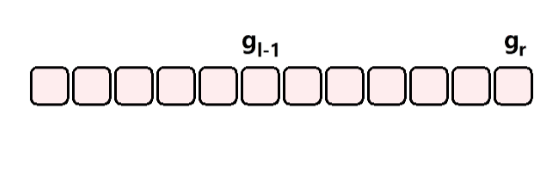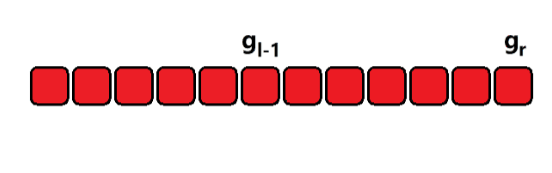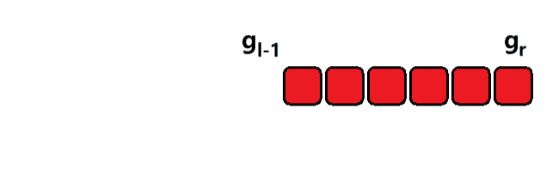
- 假设 [ 0 , x ] [0, x] [0,x] 内的 g o o d n u m b e r good \ number good number 数量为 g x g_x gx,那么区间 [ l , r ] [l, r] [l,r] 内的数量就是 g r − g l − 1 g_r - g_{l-1} gr−gl−1;分别用同样的方法求出 g r g_r gr 和 g l − 1 g_{l-1} gl−1,再相减即可;
图二-2-1
2)数位性质
- 如果一个数字 i i i 满足 i < x i < x i<x,那么 i i i 从高到低肯定出现某一位,使得这一位上的数值小于 x x x 对应位上的数值,并且之前的所有高位都和 x x x 上的位相等。
- 举个例子,当 x = 1314 x = 1314 x=1314 时, i = 0 a b c i=0abc i=0abc、 i = 12 a b i=12ab i=12ab、 i = 130 a i=130a i=130a、 i = 1312 i=1312 i=1312,那么对于 i i i 而言,无论后面的字母取什么数字,都是满足 i < x i < x i<x 这个条件的。
- 如图二-2-2所示:
图二-2-2 - 如果我们要求 g 1314 g_{1314} g1314 的值,可以通过枚举高位:当最高位为0,那么问题就转化成 g 999 g_{999} g999 的子问题;当最高位为1,问题就转化成 g 314 g_{314} g314 的子问题。
- g 314 g_{314} g314 可以继续递归求解,而 g 999 g_{999} g999 由于每一位数字范围都是 [ 0 , 9 ] [0,9] [0,9],可以转换成一般的动态规划问题来求解。
3)前缀状态
- 这里的前缀状态就对应了之前提到的 某些条件;
- 在这个问题中,前缀状态的描述为:一个数字前缀的各位数字之和对10取余(模)的值。
- 前缀状态的变化过程如图二-2-3所示:

图二-2-3 - 在【例题1】中,前缀状态的含义是:对于一个数 520 ,我们不需要记录 520 ,而只需要记录 7;对于 52013,我们不需要记录 52013,而只需要记录 1。这样就把原本海量的状态,变成了最多 10 个状态。
3、状态分析
1)状态定义
- 根据以上的三个信息,我们可以从高位到低位枚举数字 i i i 的每一位,逐步把问题转化成小问题求解。
- 我们可以定义 f ( n , s t , l i m ) f(n, st, lim) f(n,st,lim) 表示剩下还需要考虑 n n n 位数字,前面已经枚举的高位组成的前缀状态为 s t st st,且用 l i m lim lim 表示当前第 n n n 位是否能够取到最大值(对于 b b b 进制,最大值就是 b − 1 b-1 b−1,比如 10 进制状态下,最大值就是 9) 时的数字个数。我们来仔细解释一下这三维代表的含义:
- 1)当前枚举的位是 n n n 位, n n n 大的代表高位,小的代表低位;
- 2) s t st st 就是前缀状态,在这个问题中,代表了所有已经枚举的高位(即数字前缀)的各位数字之和对10取余(模)。注意:我们并不关心前缀的每一位数字是什么,而只关心它们加和模10之后的值是什么。

图二-3-1 - 3) l i m = t r u e lim=true lim=true 表示的是已经枚举的高位中已经出现了某一位比给定 x x x 对应位小的数,那么后面枚举的每个数最大值就不再受 x x x 控制;否则,最大值就应该是 x x x 的对应位。举例说明,当十进制下的数 x = 1314 x = 1314 x=1314 时,枚举到高位前三位为 “131”, l i m = f a l s e lim = false lim=false, 那么第四位数字的区间取值就是 [ 0 , 4 ] [0,4] [0,4];而枚举到高位前三位为 “130” 时, l i m = t r u e lim = true lim=true,那么第四位数字的区间取值就是 [ 0 , 9 ] [0, 9] [0,9]。参考 图二-2-2 加深理解。
2)状态转移
- 所以,我们根据以上的状态,预处理 x x x 的每个数位,表示成十进制如下:
- x = d n d n − 1 . . . d 1 x = d_nd_{n-1}...d_1 x=dndn−1...d1
- (其中 d n d_n dn 代表最高位, d 1 d_1 d1 代表最低位)
- 得出状态转移方程如下:
- f ( n , s t , l i m ) = ∑ k = 0 m a x v f ( n − 1 , ( s t + k ) m o d 10 , l i m o r ( k < m a x v ) ) \begin{aligned}& f(n, st, lim) \\ &= \sum_{k=0}^{maxv} f(n-1, (st+k) \mod 10, lim \ or \ (k < maxv))\end{aligned} f(n,st,lim)=k=0∑maxvf(n−1,(st+k)mod10,lim or (k<maxv))
- k k k 表示第 n n n 位取什么数字,它的范围是 [ 0 , m a x v ] [0, maxv] [0,maxv];
- m a x v maxv maxv 表示第 n n n 位能够取到的最大值,它由 l i m lim lim 决定,即:
- m a x v = { 9 l i m = t r u e d n l i m = f a l s e maxv = \begin{cases}9 & lim = true\\d_n & lim = false\end{cases} maxv={ 9dnlim=truelim=false
3)初始状态
- 利用上述的状态转移方程,我们可以进行递归求解,并且当 n = 0 n=0 n=0 的时候为递归出口,由于数字要求满足所有数字位数之和为 10 10 10 的倍数,所以只有 s t = 0 st = 0 st=0 的情况为合法状态,换言之,当 n = 0 n=0 n=0 时,有:
- f ( 0 , x , l i m ) = { 1 x = 0 0 0 < x ≤ 9 f(0, x, lim) = \begin{cases} 1 & x = 0\\ 0 & 0 \lt x \le 9\end{cases} f(0,x,lim)={ 10x=00<x≤9
- 而我们需要求的,就是 f ( n , 0 , f a l s e ) f(n, 0, false) f(n,0,false)。
4)记忆化
- 我们发现,如果按照以上的状态转移进行求解,会导致一个问题,就是会有很多重叠子问题,所以需要进行记忆化,比较简单的方法就是用一个三维数组 f [ n ] [ s t ] [ l i m ] f[n][st][lim] f[n][st][lim] 来记忆化。
- 当然,这里有一个技巧,就是 l i m lim lim 这个变量只有 t r u e true true、 f a l s e false false 两种取值,并且当它为 f a l s e false false 时,代表之前枚举的数的高位和所求区间 [ 0 , x ] [0, x] [0,x] 右端点中的 x x x 的高位保持完全一致,所以当 l i m = f a l s e lim = false lim=false 时,深度优先搜索树的分支最多只有 1 1 1 条,所以无须记忆化,每次直接算就可以。如图二-3-2所示的蓝色结点,就是那条唯一分支。

图二-3-2 - 综上所述,我们只需要用 f [ n ] [ s t ] f[n][st] f[n][st] 表示长度为 n n n,且每个数字的范围为 [ 0 , m a x v ] [0, maxv] [0,maxv],且前缀状态为 s t st st 的数字个数(这里 m a x v maxv maxv 和进制有关,如果是 b b b 进制,那么 m a x v = b − 1 maxv = b - 1 maxv=b−1)。
- f ( n , s t , f a l s e ) f(n, st, false) f(n,st,false) 采用普通深搜, f ( n , s t , t r u e ) f(n, st, true) f(n,st,true) 采用记忆化搜索。
三、数位 DP 代码实现
数位 DP 计算过程主要分为以下几步:
1、状态初始化
2、数位初始化
3、记忆化搜索
1、状态初始化
- 状态初始化主要是初始化 f [ n ] [ s t ] f[n][st] f[n][st] 数组,将数组中的所有值都初始化为一个小于 0 的数即可,一般用 -1。
- c++ 代码实现如下:
const int maxl = 20;
const int maxstate = 10;
const int inf = -1;
#define ll long long
ll f[maxl][maxstate];
void init() {
memset(f, inf, sizeof(f));
}
2、数位初始化
- 数位初始化就是将给定的区间 [ 0 , x ] [0, x] [0,x] 的右端点 x x x 按照数位分解到数组 d [ ] d[] d[] 中;
- 需要注意的是处理边界情况: x < 0 x \lt 0 x<0 以及 x = 0 x = 0 x=0 的情况;
- c++ 代码实现如下:
const int base = 10;
ll g(ll x) {
if (x < 0) return 0;
if (x == 0) return 1;
int d[maxl];
int n = 0;
while (x) {
d[++n] = x % base;
x /= base;
}
return dfs(n, 0, false, d);
}
3、记忆化搜索
- 记忆化搜索部分就是数位 DP 的核心实现,先给出代码,再来解释代码的含义:
ll dfs(int n, stType state, bool lim, int d[]) {
if(n == 0)
return isEndStateValid(state) ? 1 : 0; // 1)
ll sum = f[n][state];
if(lim && sum != inf) return sum; // 2)
sum = 0;
int maxv = lim ? base - 1 : d[n]; // 3)
for(int k = 0; k <= maxv; ++k) {
stType st = nextState(state, k);
bool nextlim = (k < maxv) || lim;
sum += dfs(n-1, st, nextlim, d); // 4)
}
if(lim) f[n][state] = sum; // 5)
return sum;
}
- 1)当 n = 0 n = 0 n=0 的时候,即为递归出口,也就是所有的数位都已经枚举完毕,这时候通过 所有数字之和对 10 取余数的值来判断是否是一个题目中要求的数,是则返回 1,否则返回 0;通过
isEndStateValid(state)进行判定:
#define stType int
bool isEndStateValid(stType state) {
return state == 0;
}
- 2)当
lim = true,表示接下来所有数的取值都不受给定的 x x x 限制,这时候如果f[n][state]已经计算过了,则直接返回即可; - 3)通过
lim来决定当前第 n n n 位数字枚举的上限:当lim = true时,上限为base-1;否则,为 d n d_n dn; - 4)这一步主要做状态转移,封装出一个
nextState(state, k)函数来生成当前位取 k k k 时的下一步的状态,对于【例题1】来说,函数实现如下:
stType nextState(stType st, int digit) {
return (st + digit) % 10;
}
- 5)当
lim = true,进行记忆化操作,和步骤 (2)相照应; - 通过【例题1】,我们了解了一下 数位 DP 的大致求解过程,这个题也是最简单的,接下来我们来看下竞赛中一般会遇到什么样的问题。你会发现,除了状态设计和状态转移部分的差别,整体框架代码都是不变的,所以说 数位DP 就是模板题。
四、数位 DP 进阶
1、非法状态
- 所谓非法状态,就是对于某个数字,在它的某个前缀已经能够判定这个数不满足给定题目的条件时,无须继续往下枚举,而这个前缀状态被称为非法状态,我们通过【例题2】来理解下非法状态的实际含义。
【例题2】对于一个数字,如果出现 4 或者 62 ,则属于不吉利数字,给定 l , r ( 0 < l < r < 1 0 6 ) l, r(0 \lt l \lt r < 10^6) l,r(0<l<r<106),求区间 [ l , r ] [l, r] [l,r] 中非不吉利数字的个数。
- 对于任意一个在区间 [ l , r ] [l, r] [l,r] 内的数,它的某个前缀的最后一位数字只要是 “4” 或者 最后两位数字只要是 “62” 就一定不是我们要求的数,换言之,只要一个数的前缀以 “4” 或者 “62” 结尾,那么就一定是非法前缀状态,简称非法状态。
- 前缀状态 s t st st 表示:已经枚举的数字的前缀的最后一位,所以合法的状态总共有 9 种情况:分别是以 0、1、2、3、5、6、7、8、9 结尾的,然后对所有合法状态,增加一位 [ 0 , 9 ] [0,9] [0,9] 的数字后进行状态转移;状态转移过程中会出现两种非法状态:
- 1)新增加的位等于 4;
- 2) s t = 6 st = 6 st=6,且新增加的位等于 2;
- 除了非法状态不进行状态转移,其它状态都进行状态转移,我们只需要在 【例题1】的 数位 DP 代码基础上,修改
nextstate和isEndStateValid函数即可。 - c++ 代码实现如下:
const int invalidstate = -123456789;
bool isEndStateValid(stType state) {
return true;
}
stType nextState(stType st, int digit) {
if( (digit == 4) || (st == 6 && digit == 2) ) {
return invalidstate;
}
return digit;
}
- 状态转移如图四-1-1所示:

图四-1-1 - 图中红色状态代表非法状态,蓝色状态代表任意的合法状态。当一个以 3 结尾的数字,增加一位 6,再增加一位 2,则变成非法状态,无法再进行状态转移,同样,增加一位 4,也能直接变成非法状态。而一个以 6 结尾的数字,增加一位 3,则又回到了 3 的状态。
- 可以定义一个和所有状态变量不重复的常量(一般可以用负数,如 -123456789)来表示非法状态。
2、饱和状态
- 所谓饱和状态,就是对于某个数字,在它的某个前缀已经能够判定这个数满足给定题目的条件,而这个前缀状态被称为饱和状态,我们通过【例题3】来理解下饱和状态的实际含义。
【例题3】给定一个 n ( 1 ≤ n ≤ 2 63 − 1 ) n(1 \le n \le 2^{63}-1) n(1≤n≤263−1),求小于等于 n n n 的数字中包含 49 的数的个数。
- 从题意可以得知,饱和状态 和 非法状态 正好是两个逆状态。
- 对于任意一个小于等于 n n n 的数,它的某个前缀的最后两位数字只要是 “49” 就一定是我们要求的数,换言之,只要一个数的前缀以 “49” 结尾,那么就一定是饱和前缀状态,简称饱和状态。饱和状态,无论接收什么数字,还是保持饱和状态不变。
- 前缀状态 s t st st 表示:已经枚举的数字的前缀的最后一位,所以合法的状态总共有 10 种情况:分别是以 0、1、2、3、4、5、6、7、8、9 结尾的,然后对所有合法状态,增加一位 [ 0 , 9 ] [0,9] [0,9] 的数字后进行状态转移;状态转移过程中会出现一种饱和状态:
- 1) s t = 4 st = 4 st=4,且新增加的位等于 9;
- 当某个状态变成饱和状态的那一刻,它前缀的最后一位也是9,为了区别原先的 9,我们可以用 10 进行编码,我们只需要在 【例题1】的 数位 DP 代码基础上,修改
nextstate和isEndStateValid函数即可。 - c++ 代码实现如下:
const int saturatedstate = 10;
bool isEndStateValid(stType state) {
return (state == saturatedstate);
}
stType nextState(stType st, int digit) {
if(st == 4 && digit == 9) {
st = saturatedstate;
}else if(st != saturatedstate){
st = digit;
}
return st;
}
- 状态转移如图四-2-1所示:

图四-2-1 - 图中黄色状态代表饱和状态,蓝色状态代表任意的合法状态。当一个以 3 结尾的数字,增加一位 4,再增加一位 9,则变成饱和状态,无论怎么状态转移都回到自己;而一个以 4 结尾的数字,增加一位 3,则又回到了 3 的状态。
- 可以定义一个和所有状态变量不重复的常量来表示饱和状态,由于饱和状态也是要进行记忆化的,所以不能用负数。
3、组合状态
- 所谓组合状态,就是几种不同维度的状态,通过整数编码映射到一个整数中,方便计算。
【例题4】一个数的十进制包含子串 “13” 并且能被 13 整除,则被称为 B 数,求小于等于 n ( n ≤ 1 0 9 ) n(n \le 10^9) n(n≤109) 的 B 数。
- 心里没有点 B 数,说的就是这道题了。
- 这个问题既要满足 饱和 又要满足 同余。
- 所以对于这个问题,我们发现,前缀状态 s t st st 由两部分组成:
- 1)已经枚举的数字的前缀的最后一位;
- 2)已经枚举的数字前缀模 13 的值;
- 对于第(1)种情况而言,前缀最后一位总共 0、1、2、3、4、5、6、7、8、9 这 10 种情况,并且当之前一位是 1,再枚举一个 3 时,数字达到饱和状态,可以用 10 编码;而对于第(2)种情况,可以参考 【例题1】 直接采用取模的方式,总共 13 种;
- 那么,我们可以把 (1) 和 (2) 组合起来编码,编码成一个四位的十进制数。
- 例如:前缀最后一位为 4,且所有前缀数字之和模13 为 9,则可以用 409 来表示状态,最大的状态表示为 1012。
- 同样,我们只需要在 【例题1】的 数位 DP 代码基础上,修改
nextstate和isEndStateValid函数即可。 - c++ 代码实现如下:
const int invalidstate = -123456789;
const int saturatedstate = 10;
const int mod = 13;
bool isEndStateValid(stType state) {
return (state == saturatedstate * 100 + 0);
}
stType nextState(stType st, int digit) {
int high = st/100, low = st%100;
if(high == 1 && digit == 3) {
high = saturatedstate;
}else if(high != saturatedstate){
high = digit;
}
low = (low * 10 + digit) % mod;
return high * 100 + low;
}
4、前导零状态
- 为什么要引入前导零状态?【例题5】会告诉你答案。
【例题5】如果一个数的二进制表示中 0 的个数大于等于 1,则称它为 r o u n d n u m b e r round \ number round number,给定一个区间 [ a , b ] ( 1 ≤ a ≤ b ≤ 1 0 9 ) [a,b](1 \le a \le b \le 10^9) [a,b](1≤a≤b≤109),求其中 r o u n d n u m b e r round \ number round number 的个数。
- 在这个问题中,01 和 1 是同一个数,但是 01 是符合 r o u n d n u m b e r round \ number round number 的特征的,而 1 不符合,但是我们在利用数位 DP 求解的时候,如果没有处理前导零,就会把 1 误 当成 01 而统计成 r o u n d n u m b e r round \ number round number。
- 前缀状态 s t st st 表示:二进制表示的数前缀中,0的个数 减去 1的个数,所以状态范围为 [ − 32 , 32 ] [-32, 32] [−32,32]。
- 则对于任意一个状态 st,在后面加上 0 和 1 后实现状态转移;
- 由于前导零不能作为正常零统计,所以需要加入一个初始状态,即前导零状态,只要编码不在 [ − 32 , 32 ] [-32,32] [−32,32] 即可,可以用 33 33 33 来表示;
- 我们只需要在 【例题1】的 数位 DP 代码基础上,修改
nextstate和isEndStateValid函数即可。 - c++ 代码实现如下:
const int leadingzerostate = 33;
bool isEndStateValid(stType state) {
return (state >= 0) || (state == leadingzerostate);
}
stType nextState(stType st, int digit) {
if(st == leadingzerostate) {
if(digit == 0)
return leadingzerostate;
st = 0;
}
return st + (digit == 0 ? 1 : -1);
}
- 图中绿色状态代表前导零状态,蓝色状态代表任意的合法状态。前导零状态的特点是遇到 0 则回到自己。
- 对于所有前导零会影响结果的问题,我们可以采用如下通用解法:
- 1)定义 1 个不和其它状态数字重复的 前导零状态;
- 2)状态转移的时候,如果源状态是前导零状态,在遇到下一位是零的情况,则维持前导零状态;否则,进入下一状态;
- 3)结束状态时判定如果是前导零状态,则表明这个状态表示的数就是 0,进行相应的判定。
5、位压缩状态
- 一个二进制数的每一位有两种取值 [ 0 , 1 ] [0,1] [0,1],对于一些互相独立的状态,可以用一个整数来表示各个维度的组合。总共可以表示 2 n 2^n 2n 种状态。
【例题6】一个数字的十进制下的每个位都不同,则称为 S p e c i a l N u m b e r Special \ Number Special Number,求小于 n ( n < 1 0 8 ) n(n \lt 10^8) n(n<108) 的数的个数。
- 为了确保十进制数的每一位都不同,那么在没增加一位的时候,都需要判断新增的这个数字在之前的高位数字中有没有出现过,数字一共 10 种,有 和 没有是两种状态,所以最多就是 2 1 0 2^10 210 种状态。
- 前缀状态 s t st st 表示:每位数字的出现次数,例如 s t = 11 st = 11 st=11 的二进制表示为 ( 1011 ) 2 (1011)_2 (1011)2,代表的是0、1、3 这三个数字出现过,所以我们在进行状态转移的时候,遇到 0、1、3 只能进入非法状态。
- 实际实现可以采用位运算加速,我们只需要在 【例题1】的 数位 DP 代码基础上,修改
nextstate和isEndStateValid函数即可。 - c++ 代码实现如下:
bool isValidState(stType state) {
return state != leadingzerostate;
}
stType nextState(stType st, int digit) {
if(leadingzerostate == st) {
if(digit == 0)
return leadingzerostate;
st = 0;
}
if( st & (1<<digit) ) {
return invalidstate;
}
return st | (1<<digit);
}
6、二分优化
【例题7】一个数如果至少包含 3 个 6,则称为 “beast number”,给定一个 k k k, 求第 k k k 个 “beast number”。
- 假设 [ 0 , x ] [0, x] [0,x] 区间内有 g ( x ) g(x) g(x) 个满足条件的数,那么自然, g ( x ) g(x) g(x) 是 关于 x x x 的单调不降函数。
- 我们只需要求出满足 g ( x ) ≥ k g(x) \ge k g(x)≥k 的最小的 x x x 就是答案了,于是可以用 二分 x x x,数位DP 求解 g ( x ) g(x) g(x),从而找出最小的 x x x。
- 状态编码如下:
- 状态0:前缀数字最后位不是6,且未出现过连续3个6;
- 状态1:前缀数字最后位连续6的个数为1个,且未出现过连续3个6;
- 状态2:前缀数字最后位连续6的个数为2个,且未出现过连续3个6;
- 状态3:已经出现过连续3个6,饱和状态;
- 状态转移如图四-6-1所示:

图四-6-1 - 然后就是 二分答案 + 数位DP 判可行 了。
- 我们只需要在 【例题1】的 数位 DP 代码基础上,修改
nextstate和isEndStateValid函数即可。 - c++ 代码实现如下:
const int saturatedstate = 3;
bool isEndStateValid(stType state) {
return (state == saturatedstate);
}
stType nextState(stType st, int digit) {
if(st == saturatedstate) {
return saturatedstate;
}
if(digit == 6) {
return st + 1;
}
return 0;
}
五、数位 DP 总结
1、状态转移图
- 图五-1-1对四类状态进行了一个动态演示,接下来对这张图做一个简单的解释:
- 前导零状态●:接收 数字0 时回到自己,否则根据题意进入任意初始状态;
- 饱和状态●:接收任意数字都回到自己;
- 非法状态●:无法再进行状态转移;
- 其它状态●:进行正常状态转移的状态,可能到饱和状态,也可能到非法状态,但是无法回到前导零状态;
2、数位 DP 模板
- 关于 数位 DP 的内容到这里就全部结束了,如果还有不懂的问题可以留言告诉作者或者添加作者的微信公众号。
- 本文所有示例代码均可在以下 github 上找到:github.com/WhereIsHeroFrom/Code_Templates
![]()
六、数位 DP 相关题集整理
| 题目链接 | 难度 | 解析 |
|---|---|---|
| HDU 5965 扫雷 | ★☆☆☆☆ | 无数位限制的简单数位 DP |
| HDU 4608 I-number | ★☆☆☆☆ | 比较水 |
| HDU 4722 Good Numbers | ★☆☆☆☆ | 【例题1】同余 |
| HDU 2089 不要62 | ★☆☆☆☆ | 【例题2】非法状态 |
| LeetCode 600 不含连续1的非负整数 | ★☆☆☆☆ | 非法状态 |
| HDU 3555 Bomb | ★★☆☆☆ | 【例题3】饱和状态 |
| HDU 3652 B-number | ★☆☆☆☆ | 【例题4】饱和状态 + 同余 |
| PKU 3252 Round Numbers | ★★☆☆☆ | 【例题5】前导零状态 |
| PKU 3286 How many 0’s? | ★★☆☆☆ | 前导零状态 |
| LeetCode 233 数字 1 的个数 | ★★☆☆☆ | 前导零状态 |
| HDU 3485 Count 101 | ★★☆☆☆ | 非法状态 |
| HDU 3284 Adjacent Bit Counts | ★★☆☆☆ | 非法状态 |
| HDU 1663 The Counting Problem | ★★☆☆☆ | 前导零状态 |
| 洛谷 P2602 数字计数 | ★★☆☆☆ | 前导零状态 |
| 洛谷 P2657 windy 数 | ★★☆☆☆ | 前导零状态 + 非法状态 |
| 洛谷 P3413 萌数 | ★★☆☆☆ | 饱和状态 + 前导零状态 |
| 洛谷 P6754 Palindrome-Free Numbers | ★★☆☆☆ | 非法状态 + 前导零状态 |
| 洛谷 P4317 花神的数论题 | ★★☆☆☆ | 二分快速幂 + 数位DP |
| HDU 5898 odd-even number | ★★☆☆☆ | 前导零状态 + 非法状态 |
| HDU 6148 Valley Numer | ★★☆☆☆ | 非法状态 + 前导零状态 |
| 洛谷 P6371 V | ★★★☆☆ | 同余 + 分情况讨论 |
| HDU 4734 F(x) | ★★★☆☆ | 预处理 + 剪枝 |
| HDU 4151 The Special Number | ★★★☆☆ | 【例题6】位压缩 + 非法状态 + 前导零状态 |
| HDU 5179 beautiful number | ★★★☆☆ | 位压缩 + 前导零状态 |
| 洛谷 P4124 手机号码 | ★★★☆☆ | 位压缩 + 前导零状态 |
| 洛谷 CF855E Salazar Slytherin’s Locket | ★★★☆☆ | 位压缩 + 前导零状态 |
| PKU 3208 Apocalypse Someday | ★★★☆☆ | 【例题7】二分 + 饱和状态 |
| HDU 2867 Continuous Digit | ★★★☆☆ | PKU 3208 的一般情况 |
| HDU 3271 SNIBB | ★★★☆☆ | 二分 + 求和 |
| HDU 2889 Without Zero | ★★★☆☆ | 二分 + 非法状态 |
| HDU 3943 K-th Nya Number | ★★★☆☆ | 二分 + 非法状态 |
| PKU 3971 Scales | ★★★☆☆ | 进位模拟 |
| 洛谷 P4127 同类分布 | ★★★☆☆ | 枚举 + 同余 |
| HDU 5787 K-wolf Number | ★★★☆☆ | 状态压缩 + 前导零状态 |
| HDU 3709 Balanced Number | ★★★☆☆ | 推导 + 前导零状态 |
| HDU 3967 Zero’s Number | ★★★☆☆ | 组合状态 |
| HDU 5676 ztr loves lucky numbers | ★★★☆☆ | 二分 + 数位DP |
| HDU 5456 Matches Puzzle Game | ★★★★☆ | 数位 DP 进阶题 |
| 洛谷 CF55D Beautiful numbers | ★★★★☆ | 最小公倍数 + 数位 DP |
| HDU 4507 吉哥系列故事——恨7不成妻 | ★★★★☆ | 数论 + 数位DP |
| HDU 4352 XHXJ’s LIS | ★★★★☆ | 最长递增子序列 + 数位DP |
| PKU 3986 Math teacher’s homework | ★★★★★ | 位运算 + 数位DP |