FZU 1096 QS Network
QS Network
64-bit integer IO format: %I64d Java class name: Main
In the planet w-503 of galaxy cgb, there is a kind of intelligent creature named QS. QScommunicate with each other via networks. If two QS want to get connected, they need to buy two network adapters (one for each QS) and a segment of network cable. Please be advised that ONE NETWORK ADAPTER CAN ONLY BE USED IN A SINGLE CONNECTION.(ie. if a QS want to setup four connections, it needs to buy four adapters). In the procedure of communication, a QS broadcasts its message to all the QS it is connected with, the group of QS who receive the message broadcast the message to all the QS they connected with, the procedure repeats until all the QS's have received the message.
A sample is shown below:
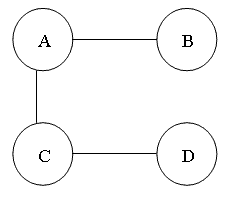
A sample QS network, and QS A want to send a message.
Step 1. QS A sends message to QS B and QS C;
Step 2. QS B sends message to QS A ; QS C sends message to QS A and QS D;
Step 3. the procedure terminates because all the QS received the message.
Each QS has its favorate brand of network adapters and always buys the brand in all of its connections. Also the distance between QS vary. Given the price of each QS's favorate brand of network adapters and the price of cable between each pair of QS, your task is to write a program to determine the minimum cost to setup a QS network.
Input
The 1st line of the input contains an integer t which indicates the number of data sets.
From the second line there are t data sets.
In a single data set,the 1st line contains an interger n which indicates the number of QS.The 2nd line contains n integers, indicating the price of each QS's favorate network adapter.
In the 3rd line to the n+2th line contain a matrix indicating the price of cable between ecah pair of QS.
Constrains:
All the integers in the input are non-negative and not more than 1000.Output
for each data set,output the minimum cost in a line. NO extra empty lines needed.
Sample Input
1 3 10 20 30 0 100 200 100 0 300 200 300 0
Sample Output
370
解题:需要注意:每个网络适配器只能用于单一的通信中

1 #include <iostream> 2 #include <cstdio> 3 #include <queue> 4 #include <cstring> 5 #define INF 0x3f3f3f3f 6 #define pii pair<int,int> 7 using namespace std; 8 const int maxn = 1010; 9 struct arc{ 10 int to,w,next; 11 arc(int x = 0,int y = 0,int z = -1){ 12 to = x; 13 w = y; 14 next = z; 15 } 16 }e[maxn*maxn]; 17 int head[maxn],d[maxn],adapter[maxn],tot,n; 18 bool done[maxn]; 19 priority_queue< pii,vector< pii >,greater< pii > >q; 20 void add(int u,int v,int w){ 21 e[tot] = arc(v,w,head[u]); 22 head[u] = tot++; 23 } 24 int prim(){ 25 int ans = 0; 26 for(int i = 0; i < maxn; ++i){ 27 d[i] = INF; 28 done[i] = false; 29 } 30 while(!q.empty()) q.pop(); 31 q.push(make_pair(d[0] = 0,0)); 32 while(!q.empty()){ 33 int u = q.top().second; 34 q.pop(); 35 if(done[u]) continue; 36 done[u] = true; 37 ans += d[u]; 38 for(int i = head[u]; ~i; i = e[i].next){ 39 if(d[e[i].to] > e[i].w) q.push(make_pair(d[e[i].to] = e[i].w,e[i].to)); 40 } 41 } 42 return ans; 43 } 44 int main(){ 45 int kase; 46 scanf("%d",&kase); 47 while(kase--){ 48 memset(head,-1,sizeof(head)); 49 int ans = tot = 0,tmp; 50 scanf("%d",&n); 51 for(int i = 0; i < n; ++i) 52 scanf("%d",adapter+i); 53 for(int i = 0; i < n; ++i){ 54 for(int j = 0; j < n; ++j){ 55 scanf("%d",&tmp); 56 if(i != j) add(i,j,tmp+adapter[i]+adapter[j]); 57 } 58 } 59 printf("%d\n",prim()); 60 } 61 return 0; 62 }
