1. 回顾拉格朗日乘数法
想象一下,目标函数是一座山的高度,约束
是镶嵌在山上的一条曲线如下图。
为了找到曲线上的最低点,就从最低的等高线(0那条)开始网上数。数到第三条,等高线终于和曲线有交点了(如上图所示)。因为比这条等高线低的地方都不在约束范围内,所以这肯定是这条约束曲线的最低点了。
而且约束曲线在这里不可能和等高线相交,一定是相切。因为如果是相交的话,如下图所示,那么曲线一定会有一部分在B区域,但是B区域比等高线低,这是不可能的。
两条曲线相切,意味着他们在这点的法线平行,也就是法向量只差一个任意的常数乘子(取为
, 我们把这个式子的右边移到左边,并把常数移进微分算子,就得到
把这个式子重新解释一下,这个就是函数
无约束情况下极值点的充分条件
2. 回顾对偶问题
更多信息见
https://www.camdemy.com/media/1585
证明见
http://sma.epfl.ch/~niemeier/opt09/opt09_ch05.pdf
https://www.cs.cmu.edu/afs/cs.cmu.edu/academic/class/15859-f11/www/notes/lecture05.pdf
优化原问题和其对偶问题
本来是有约束的极值问题,可以转换为其对偶问题的无约束极值问题
优化理论系列1——拉格朗日对偶及强弱定理证明
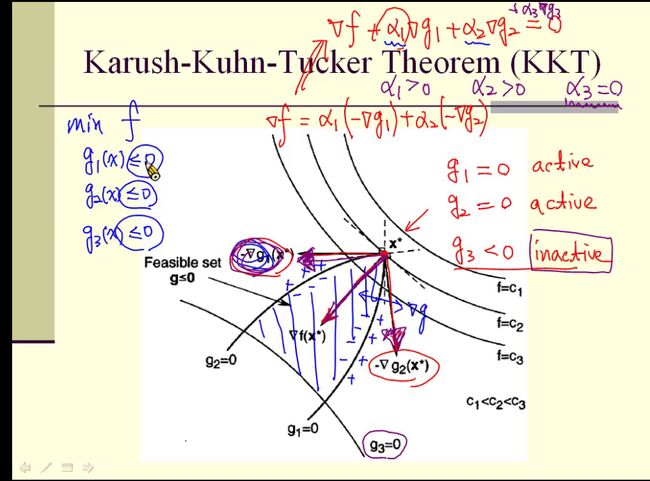
3. 回顾 Karush-Kuhn-Tucker(KKT)
那么针对不等式的约束如何处理呢?
KKT是用来解释哪些点是重要的,即找到support vector
梯度是变化率最大的方向
针对极值x来说,可以看到
g1=0,(active constraint),
g2=0,(active constraint),
g3<0,(inactive constraint),
对于,(active constraint),我们认为对于确定极值是有用的,而(Inactive constraint)我们认为对确定极值是没有用的。
x的梯度方向可以用g1,g2的负梯度方向来表示。此时a1>0,a2>0.
若将x*的梯度方向可以用g1,g2的负梯度方向和g3的梯度方向来表示,则此时a1>0,a2>0,a3=0.
也就是说针对哪些有用的active constraint,他们的拉格朗日系数大于零,而针对哪些无用的inactive constraint,他们的拉格朗日系统等于0.
由三式可知,若拉格朗日系数a>0,则相应的g=0,即为active constraint,为有用的约束,也就是这些约束点为支撑向量点,落在g=0上。
若g<0,则a=0,即为inactive constraint,无用的约束,则这些点不是支撑向量点。
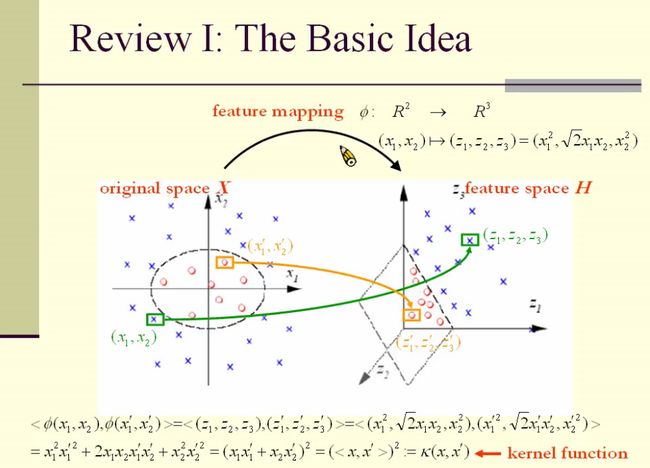
4. Feature mapping
特征映射从低维空间映射到高维空间,便于“线性可分”
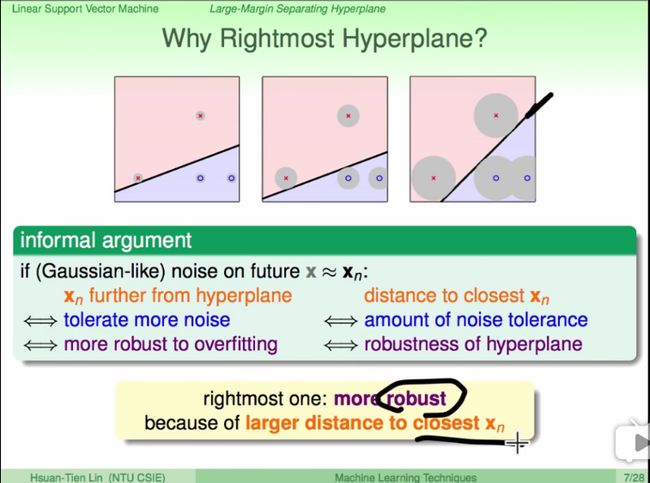
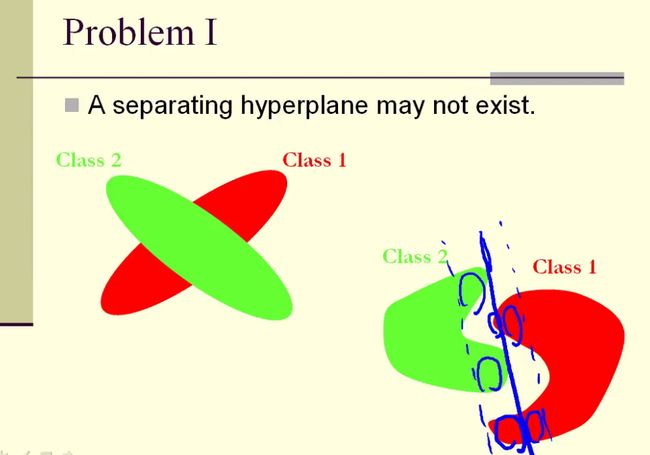
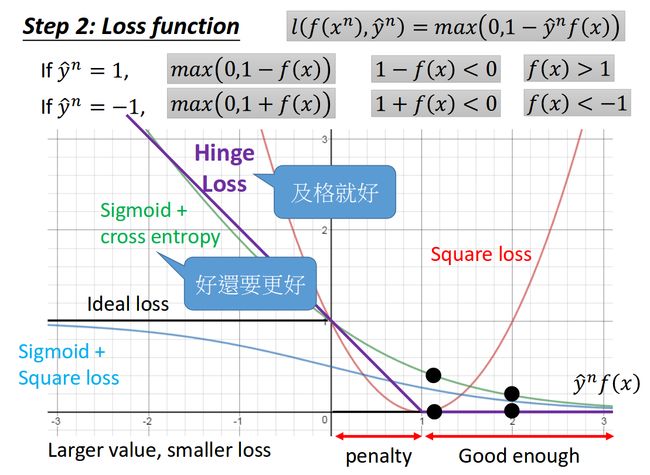
5. SVM的思想起源
在感知机模型中,我们可以找到多个可以分类的超平面将数据分开,并且优化时希望所有的点都离超平面远。但是实际上离超平面很远的点已经被正确分类,我们让它离超平面更远并没有意义。反而我们最关心是那些离超平面很近的点,这些点很容易被误分类。如果我们可以让离超平面比较近的点尽可能的远离超平面,那么我们的分类效果会好有一些。
支持向量机(Support Vector Machine)是Cortes和Vapnik于1995年首先提出的,它在解决小样本、非线性及高维模式识别中表现出许多特有的优势,并能够推广应用到函数拟合等其他机器学习问题中。
找到对局部扰动“容忍”性最好的超平面是最优超平面。
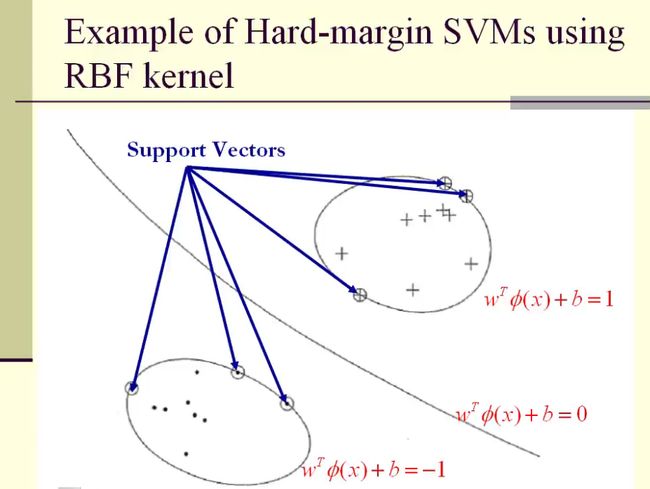
6. Hard-Margin
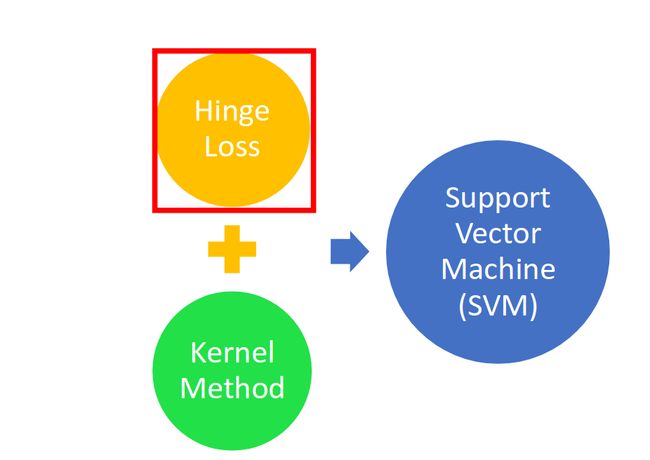
Kernel Lagrange
Quadratic Problem
How to find "b"
7. Soft-Margin:
容忍一些误差,也就是说一些样本会落在最大间隔两边支持向量边界的内部。
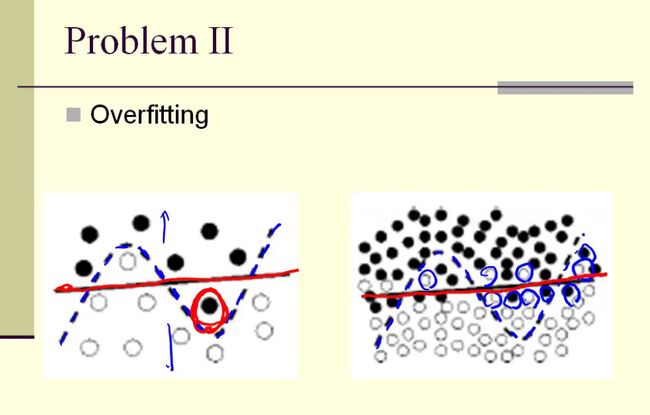
overfitting的问题,小样本容易出现overfitting,样本不具备代表性。
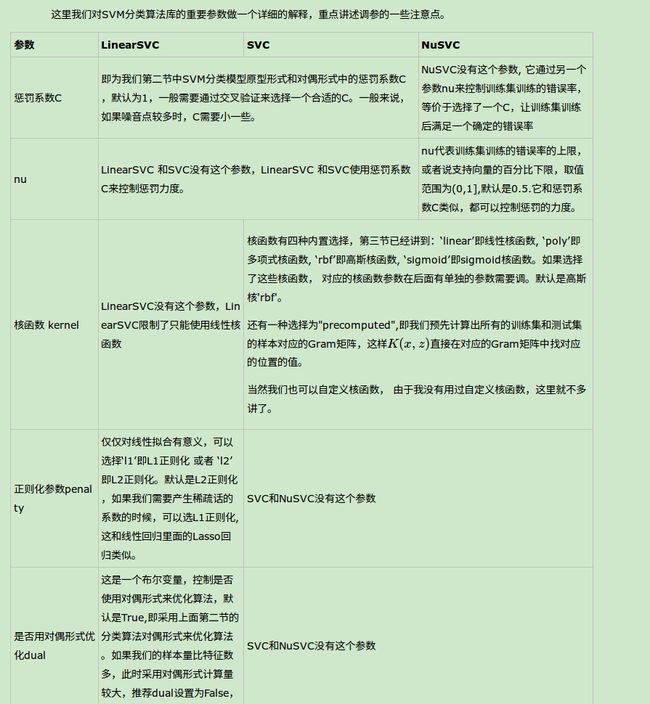
scikit-learn 支持向量机算法库使用小结
支持向量机高斯核调参小结
本文从实践的角度对scikit-learn SVM算法库的使用做一个小结。scikit-learn SVM算法库封装了libsvm 和 liblinear 的实现,仅仅重写了算法了接口部分。
- scikit-learn SVM算法库使用概述
scikit-learn中SVM的算法库分为两类,一类是分类的算法库,包括SVC, NuSVC,和LinearSVC 3个类。另一类是回归算法库,包括SVR, NuSVR,和LinearSVR 3个类。相关的类都包裹在sklearn.svm模块之中。
对于SVC, NuSVC,和LinearSVC 3个分类的类,SVC和 NuSVC差不多,区别仅仅在于对损失的度量方式不同,而LinearSVC从名字就可以看出,他是线性分类,也就是不支持各种低维到高维的核函数,仅仅支持线性核函数,对线性不可分的数据不能使用。
同样的,对于SVR, NuSVR,和LinearSVR 3个回归的类, SVR和NuSVR差不多,区别也仅仅在于对损失的度量方式不同。LinearSVR是线性回归,只能使用线性核函数。
我们使用这些类的时候,如果有经验知道数据是线性可以拟合的,那么使用LinearSVC去分类 或者LinearSVR去回归,它们不需要我们去慢慢的调参去选择各种核函数以及对应参数, 速度也快。如果我们对数据分布没有什么经验,一般使用SVC去分类或者SVR去回归,这就需要我们选择核函数以及对核函数调参了。
什么特殊场景需要使用NuSVC分类 和 NuSVR 回归呢?如果我们对训练集训练的错误率或者说支持向量的百分比有要求的时候,可以选择NuSVC分类 和 NuSVR 。它们有一个参数来控制这个百分比。
这些类的详细使用方法我们在下面再详细讲述。
- 回顾SVM分类算法和回归算法
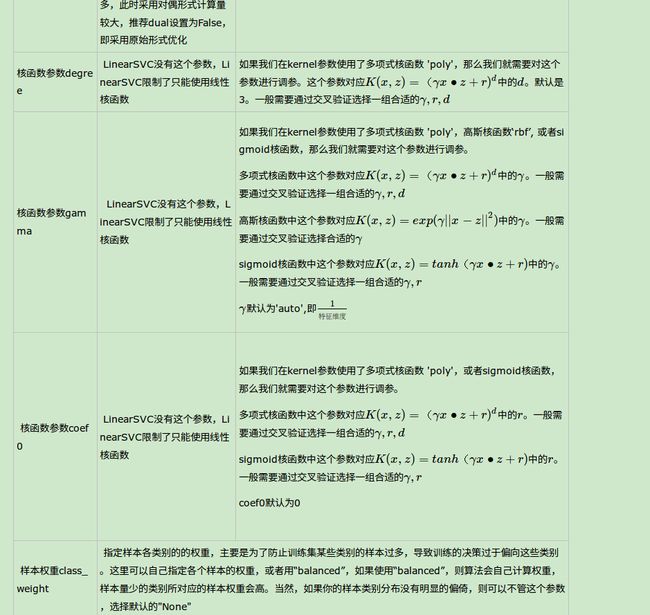
- SVM核函数概述
在scikit-learn中,内置的核函数一共有4种,当然如果你认为线性核函数不算核函数的话,那就只有三种。
1)线性核函数(Linear Kernel)表达式为:K(x,z)=x∙z
,就是普通的内积,LinearSVC 和 LinearSVR 只能使用它。
2) 多项式核函数(Polynomial Kernel)是线性不可分SVM常用的核函数之一,表达式为:K(x,z)=(γx∙z+r)d
,其中,γ,r,d
都需要自己调参定义,比较麻烦。
3)高斯核函数(Gaussian Kernel),在SVM中也称为径向基核函数(Radial Basis Function,RBF),它是libsvm默认的核函数,当然也是scikit-learn默认的核函数。表达式为:K(x,z)=exp(γ||x−z||2)
, 其中,γ
大于0,需要自己调参定义。
4)Sigmoid核函数(Sigmoid Kernel)也是线性不可分SVM常用的核函数之一,表达式为:K(x,z)=tanh(γx∙z+r)
, 其中,γ,r
都需要自己调参定义。
一般情况下,对非线性数据使用默认的高斯核函数会有比较好的效果,如果你不是SVM调参高手的话,建议使用高斯核来做数据分析。
-
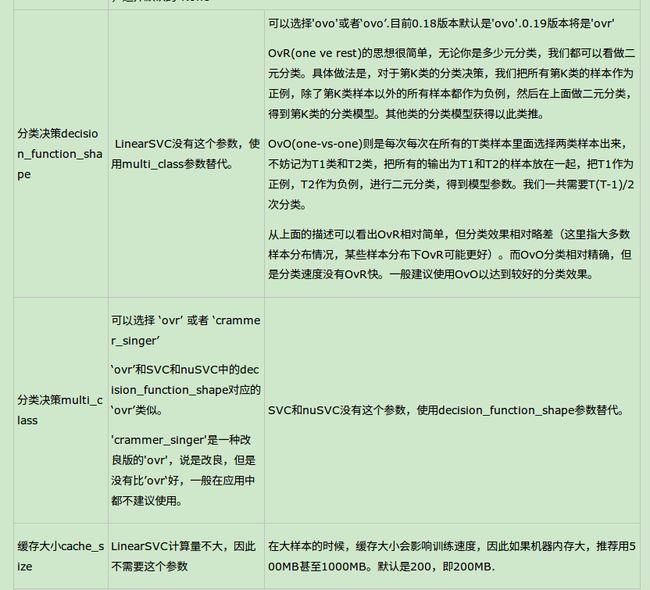
SVM分类算法库参数小结
- SVM回归算法库参数小结
- SVM算法库其他调参要点
上面已经对scikit-learn中类库的参数做了总结,这里对其他的调参要点做一个小结。
1)一般推荐在做训练之前对数据进行归一化,当然测试集中的数据也需要归一化。。
2)在特征数非常多的情况下,或者样本数远小于特征数的时候,使用线性核,效果已经很好,并且只需要选择惩罚系数C即可。
3)在选择核函数时,如果线性拟合不好,一般推荐使用默认的高斯核'rbf'。这时我们主要需要对惩罚系数C和核函数参数γ 进行艰苦的调参,通过多轮的交叉验证选择合适的惩罚系数C和核函数参数γ。
4)理论上高斯核不会比线性核差,但是这个理论却建立在要花费更多的时间来调参上。所以实际上能用线性核解决问题我们尽量使用线性核。
SVM调参
SVM模型有两个非常重要的参数C与gamma。其中 C是惩罚系数,即对误差的宽容度。c越高,说明越不能容忍出现误差,容易过拟合。C越小,容易欠拟合。C过大或过小,泛化能力变差。
gamma是选择RBF函数作为kernel后,该函数自带的一个参数。隐含地决定了数据映射到新的特征空间后的分布,gamma越大,支持向量越少,gamma值越小,支持向量越多。支持向量的个数影响训练与预测的速度。
此外大家注意RBF公式里面的sigma和gamma的关系如下:
这里面大家需要注意的就是gamma的物理意义,大家提到很多的RBF的幅宽,它会影响每个支持向量对应的高斯的作用范围,从而影响泛化性能。如果gamma设的太大,很小的高斯分布长得又高又瘦, 会造成只会作用于支持向量样本附近,对于未知样本分类效果很差,存在训练准确率可以很高,(如果让
rbf实际是记忆了若干样例,在sv中各维权重重要性等同。线性核学出的权重是feature weighting作用或特征选择
随机搜索Random search与网格搜Grid search
在沙堆上淘金,把沙堆按比例分成格子,淘了一格再去淘下一格,这是网格搜索。网格搜索其实可以理解成暴力搜索,一般当超参数的数目稍小的时候(三四个或者更少的超参数),才会用网格搜索.当超参数的数量增长时,网格搜索的计算复杂度会呈现指数增长.,用户列出一个较小的超参数值域,这些超参数值域的笛卡尔集(排列组合)为一组组超参数。网格搜索算法使用每组超参数训练模型并挑选验证集误差最小的超参数组合。
3.2. Tuning the hyper-parameters of an estimator
在沙堆上淘金,闭上眼睛每次随便选个方向走,每次再随便选个步数,走到这步数就停下来淘一把,这是随机搜索。随机搜索一般会根据超参数的边缘分布采样。为每个参数定义了一个分布函数并在该空间中采样(sampling).
Bergstra, J. and Bengio, Y., Random search for hyper-parameter optimization, The Journal of Machine Learning Research (2012)
优缺点比较:
Randomized Search指数级高效于Grid Search,因为Grid Search将大量的计算浪费在了指数级的对结果无影响的参数中,而Randomized Search几乎每次都搜索了对结果有影响的参数的值。
Grid Search网格搜索可以得到全局最优, (C,gamma)相互独立,便于并行化进行
关于深度学习中超参数优化方法中的随机搜索和网格搜索的解释?
SVM的两个参数 C 和 gamma
# -*- coding: UTF-8 -*-
from __future__ import division
#from __future__ import print_function
print("0. import dependency----------------------------------------------")
from sklearn.model_selection import validation_curve
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import LabelEncoder
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import RandomizedSearchCV
from sklearn.svm import SVC
from sklearn.ensemble import RandomForestClassifier
from scipy.stats import randint as sp_randint # 用于产生随机分布的整数
# 使用随机搜索,使用SVM分类器
def RS_SVM(X_train, y_train):
# 构造模型
pipe_svc = Pipeline([('scl', StandardScaler()),
('clf', SVC(random_state=1))])
param_range = [10 ** c for c in range(-4, 4)]
param_dist = { # 对于核SVM则需要同时调优C和gamma值
'clf__C': param_range,
'clf__gamma': param_range,
'clf__kernel': ['linear', 'rbf']
}
# run randomized search
n_iter_search = 20
random_search = RandomizedSearchCV(pipe_svc,
param_distributions=param_dist,
n_iter=n_iter_search)
random_search.fit(X_train, y_train)
report(random_search.cv_results_)
return random_search.best_estimator_
# 使用网格搜索,使用SVM分类器
def GS_SVM(X_train, y_train):
# 构造模型
pipe_svc = Pipeline([('scl', StandardScaler()),
('clf', SVC(random_state=1))])
param_range = [10**c for c in range(-4, 4)]
# param_range = np.linspace(0.0001, 1, 10)
param_grid = [
{'clf__C': param_range, 'clf__kernel': ['linear']}, # 对于线性SVM只需要调优正则化参数C
{'clf__C': param_range, 'clf__gamma': param_range, 'clf__kernel': ['rbf']} # 对于核SVM则需要同时调优C和gamma值
]
gs = GridSearchCV(estimator=pipe_svc,
param_grid=param_grid,
scoring='accuracy',
cv=10,
n_jobs=-1)
gs = gs.fit(X_train, y_train)
# print(gs.best_score_)
# print(gs.best_params_)
# 使用最优模型进行性能评估
# clf = gs.best_estimator_
# clf.fit(X_train, y_train)
# print('Test Accuracy: %.3f' % clf.score(X_test, y_test))
report(gs.cv_results_)
return gs.best_estimator_
[读书笔记] 《Python 机器学习》 - 使用RandomParameterOpt与GridSearch进行超参调整
参考文献
Hard-Margin Support Vector Machines
Soft-Margin Support Vector Machines
https://www.camdemy.com/media/1647
李政轩
《Kernel Method(A Chinese Tutorial on Kernel Method, PCA, KPCA, LDA, GDA, and SVMs)》
https://www.camdemy.com/folder/462
如果能看YouTube,裡面有更新的版本
(請找一下播放清單)
https://www.youtube.com/user/u4815977
Clustering
https://www.camdemy.com/folder/463
Scikit-learn实战之 SVM回归分析、密度估计、异常点检测
Regression
https://www.camdemy.com/folder/464
https://www.camdemy.com/folder/465
pluskid支持向量机系列
支持向量机: Maximum Margin Classifier
jerrylead支持向量机SVM
http://yuenshome.cn/?p=3023
Support Vector Machine (SVM)
http://speech.ee.ntu.edu.tw/~tlkagk/courses/ML_2016/Lecture/SVM%20(v5).pdf
《Kernel Method(A Chinese Tutorial on Kernel Method, PCA, KPCA, LDA, GDA, and SVMs)》
https://www.camdemy.com/folder/462
SVM-ipython-tutorial
支持向量机(SVM)的特点与不足
----------------------------------
SVM 简要推导过程
YichuanTang , “Deep Learning using Linear Support Vector Machines”, ICML 2013 Challenges in Representation Learning Workshop
Structured SVM
http://speech.ee.ntu.edu.tw/~tlkagk/courses/ML_2017/Lecture/Structured%20Introduction.pdf
解密SVM系列(一):关于拉格朗日乘子法和KKT条件
解密SVM系列(二):SVM的理论基础
解密SVM系列(三):SMO算法原理与实战求解
解密SVM系列(四):SVM非线性分类原理实验
解密SVM系列(五):matlab下libsvm的简单使用:分类与回归
支持向量机原理(一) 线性支持向量机
支持向量机原理(二) 线性支持向量机的软间隔最大化模型
支持向量机原理(三)线性不可分支持向量机与核函数
支持向量机原理(四)SMO算法原理
支持向量机原理(五)线性支持回归
支持向量机高斯核调参小结
scikit-learn 支持向量机算法库使用小结
零基础学SVM—Support Vector Machine(一)
零基础学SVM—Support Vector Machine(二)
SVM算法入门
支持向量机通俗导论(理解SVM的三层境界)
程序员训练机器学习 SVM算法分享
【机器学习实战07】SVM--LibSVM工具包的使用
【机器学习实战07】理解SVM
【直观详解】支持向量机SVM