C#堆栈和队列
C#堆栈和队列
此前已经采用 Array类和ArrayList类来把数据像列表一样组织在一起. 尽管这两种数据结构可以方便的把数据组织起来进行处理, 但是它们都没有为设计和实现实际问题的解决方案提供真正的抽象。
堆栈(stack)和队列(queue)是两种面向列表(list-oriented)的数据结构, 它们都提供了易于理解的抽象. 堆栈中的数据只能在表的某一端进行添加和删除操作, 反之队列中的数据则在表的一端进行添加操作而在表的另一端进行删除操作. 堆栈被广泛用于从表达式计算到处理方法调用的任何编程语言的实现中. 而队列则用在区分优先次序的操作系统处理以及模拟现实世界的事件方面, 比如银行出纳柜台的队列, 以及建筑物内电梯的操作。
C#为使用这些数据结构提供了两种类:Stack 类和Queue类. 本章将会讨论如何使用这些类并且介绍一些实用的例子。
堆栈, 堆栈的实现以及Stack 类
正如前面提到的那样, 堆栈是最频繁用到的数据结构之一. 在堆栈中, 数据项只能从表的末端进行访问. 可访问的这端被称为是栈顶. 堆栈的标准模型是自助餐厅的盘子堆. 人们始终要从顶部拿走盘子, 而且当洗碗工或者杂工把盘子放回盘子堆的时候也是把它放在盘堆的顶部. 堆栈是著名的后进先出(LIFO)数据结构.
堆栈的操作
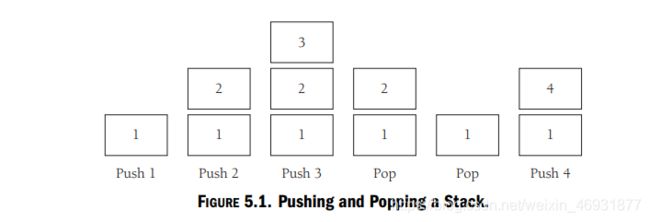
堆栈最基本的两种操作就是向堆栈内添加数据项以及从堆栈中删除数据项. Push(进栈)操作是向堆栈内添加数据项. 而把数据项从堆栈内取走则用 Pop(出栈)操作. 这些操作的实例说明可参见图5-1.
堆栈的另外一种基本操作就是察看栈顶的数据项. Pop 操作会返回栈顶的数据项, 但是此操作也会把此数据项从堆栈中移除. 如果只是希望察看栈顶的数据项而不是真的要移除它, 那么在C#中有一种名为Peek(取数)的操作可以实现. 此操作在其他语言和实现中可能采用其他的名称(比如Top). 进栈、出栈以及取数都是在使用堆栈时会执行的基本操作. 但是, 还有其他一些需要执行的操作以及需要检查的属性. 从堆栈中移除全部数据项就是非常有用的操作. 通过调用Clear(清除)操作可以把堆栈全部清空. 此外, 在任何时候都能知道堆栈内数据项的数量也是非常有用的. 这可以通过调用Count(计数)属性来实现. 许多实现都有StackEmpty 方法, 此方法会返回true或false来表示堆栈是否为空, 也可以采用Count属性达到同样的目的. .NET 框架的Stack 类实现了全部这些操作和属性, 甚至还要更多. 但是在讨论如何使用它们之前, 还是先来看看如果没有Stack 类, 则需要如何实现一个堆栈。
Stack类的实现
Stack的实现需要采用一种潜在的结构来保存数据. 为了在新数据项进栈的时候不需要考虑列表的大小, 所以这里选择用ArrayList来+ 保存数据。
因为C#拥有如此强大的面向对象的编程特征, 所以这里将把我们自定义的堆栈以类的形式来实现.
将这个类命名为CStack, 它应该包括一个构造方法以及上述提及的各种操作方法. 我们将使用"属性property"的方式来获取堆栈数据的数量, 从而演示一下C#中类的属性是如何实现的. 首先从该类需要的私有数据开始吧。
所需要的最重要的变量就是用来存储堆栈数据项的 ArrayList对象. 除此以外, 另一个需要关注的数据就是栈顶. 这里将用一个简单的整型变量来处理以便提供类似索引的功能. 当实例化一个新的CStack对象时, 通过构造方法将此变量的初始值设为-1, 每次把新的数据项入栈时, 该变量变量就加1。
入栈方法Push将调用ArrayLsit的Add 方法, 并且把传递给它的数值添加到ArrayList里面. 出栈方法Pop需要完成三件事:调用RemoveAt方法来取走栈顶的数据项, 栈顶索引变量减1, 以及最终返回出栈的对象.。Peek方法则通过调用ArrayList的Item 方法来实现. Clear方法调用ArrayList类中的同名方法. 另外由于不需要直接改变堆栈上数据项的数量, 所以Count属性设置为只读.根据上述思路, CStack代码如下:
using System.Collections;
class CStack {
//栈顶索引
private int p_index;
//在CStack类内部保存数据的ArrayList字段
private ArrayList list;
public CStack()
{
list = new ArrayList();
p_index = -1;
}
//只读属性, 返回ArrayList的元素总数
public int count {
get {
return list.Count;
}
}
//入栈
public void push(object item)
{
list.Add(item);
p_index++;
}
//出栈
public object pop()
{
object obj = list[p_index];
list.RemoveAt(p_index);
//数据出栈后栈顶改变
p_index--;
return obj;
}
public void clear()
{
list.Clear();
p_index = -1;
}
public object peek()
{
return list[p_index];
}
}
下面就用这段代码来编写一个用堆栈解决问题的程序。
首先介绍一个概念: “回文palindrome”. 回文是指向前和向后拼写都完全一样的字符串. 例如, “dad”、“madam”以及“上海自来水来自海上”都是回文, 而“来左手跟我一起画个龙”就不是回文. 检查一个字符串是否为回文的工具之一就是使用堆栈. 具体做法就是, 逐个字符的读取字符串, 并把读取的每个字符都压入堆栈. 下一步就是把堆栈内的字符依次出栈, 并每次都与原始字符中与取出次序一样的位置的字符进行比较. 如果在任何时候发现两个字符不相同, 那么此字符串就不是回文, 同时就此终止程序. 如果比较始终都相同, 那么此字符串就是回文。
既然已经定义了CStack 类, 所以下面这个程序就从Sub Main 开始:
static void Main()
{
CStack alist = new CStack();
string ch;
string word = "月下舟随舟下月";
bool isPalindrome = true;
for (int x = 0; x < word.Length; x++)
//逐个字符入栈
alist.push(word.Substring(x, 1));
//标记已经对比到字符串第几个位置了
int pos = 0;
while (alist.count > 0) {
//不断出栈, 并与字符串对应位置的字符对比
ch = alist.pop().ToString();
if (ch != word.Substring(pos, 1)) {
//友一个不一样就不算是回文
isPalindrome = false;
break;
}
pos++;
}
if (isPalindrome)
Console.WriteLine(word + "===那可是正经老回文了");
else
Console.WriteLine(word + "不是回文");
Console.Read();
}
Stack类
Stack 类是ICollection接口的一个实现. 它代表了一个LIFO群集或一个堆栈. 该类在.NET Framework中作为循环缓冲区实现, 它允许在入栈时动态分配堆栈的长度.
Stack类包含与堆栈相关的众多方法, 首先讨论下Stack类的构造方法的工作原理.
Stack构造函数方法
有三种方式来实例化一个Stack对象.
第一种, 默认的构造函数, 会实例化一个具有10 个数值初始容量的空堆栈. 调用默认构造函数的方式如下所示:
Stack myStack = new Stack();
泛型堆栈构造函数的使用方法如下所示:
Stack<string> myStack = new Stack<string>();
每次堆栈装满元素后, 容量扩充为之前的二倍大小.
第二种实例化Stack对象的方式是, 为构造函数传递一个群集对象来创建堆栈对象. 例如, 可以为堆栈的构造函数传递一个数组参数, 并基于这个数组的元素来设置堆栈对象的数据:
string[] names = new string[] {
"Raymond", "David", "Mike" };
Stack nameStack = new Stack(names);
对上方代码创建的堆栈执行出栈操作, 会首先移除"Mike".
第三种实例化堆栈对象的方式是, 通过构造函数指明堆栈的初始容量. 程序在使用这种方式创建的Stack对象时会更有效率. 如果堆栈中有20个元素, 并且它的总容量为20, 那么添加一个新元素将带来20+1个指令操作, 因为每个元素都必须移位以适应新元素(通过阅读C#微软手册Stack类, 可以知道, Stack使用一个内部数组存储数据, 所以此处的20+1个指令操作应该指的就是, 新建一个扩容的数组后, 执行复制20个原数组数据和新增1个数据到扩容后的新数组所带来的.)
实例化带有初始容量的Stack 对象的程序代码如下所示:
Stack myStack = new Stack(25);
主要的堆栈操作
对堆栈最主要的操作就是Push和Pop. 用Push方法把数据添加到堆栈里面. 用Pop方法把数据从堆栈中移除. 下面通过用堆栈来实现一些简单的数学计算, 来了解一下这些方法.
这个算数计算器采用了两个堆栈:一个用于存储运算数字, 而另一个则用于运算符号. 数学公式会作为字符串存储起来. 利用For循环来读取公式中的每个字符, 从而把字符串解析成一个个独立的记号. 如果记号是数字, 就把它压入数字堆栈内. 如果记号是运算符, 则把它压入运算符堆栈内. 既然这里采用的是中缀算术运算(中缀运算指的公式中, 计算符号都位于数字之间, 比如3+4; 与此对应的还有前缀运算和后缀运算, 有兴趣的自行百度), 所以在执行一次操作之前要等到堆栈内压入两个数字后才可以进行一次计算. 一旦满足了进行计算的条件, 就把两个运算数和一个运算符出栈, 并且根据运算符执行对应计算, 计算出的结果将被压入数字堆栈, 并作为下一个运算符的第一个运算数. 继续反复这样的操作直到所有数字都执行完入栈和出栈操作为止.
下面就是程序的代码:
//原文代码有一些纰漏 我已修改
using System;
using System.Collections.Generic;
using System.Text.RegularExpressions;
namespace csstack
{
class Class1
{
static void Main(string[] args)
{
//运算数字堆栈
Stack<int> nums = new Stack<int>();
//运算符号堆栈
Stack<string> ops = new Stack<string>();
//计算目标数学公式
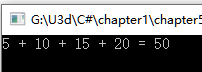
string expression = "5 + 10 + 15 + 20";
Console.Write(expression + " = ");
Calculate(nums, ops, expression);
Console.WriteLine(nums.Pop());
Console.Read();
}
//自定义的用来判断字符串是否是数字的函数
static bool IsNumeric(string input)
{
bool flag = true;
//匹配全数字的正则表达式
string pattern = (@"^\d+$");
Regex validate = new Regex(pattern);
if (!validate.IsMatch(input)) {
//如果匹配不上, 说明不是数字字符串
flag = false;
}
return flag;
}
//计算公式结果的方法
static void Calculate(Stack<int> N, Stack<string> O, string exp)
{
string ch, token = "";
for (int p = 0; p < exp.Length; p++) {
//遍历exp字符串, 一个字符一个字符的提取
ch = exp.Substring(p, 1);
if (IsNumeric(ch))
//如果是数字, 连接到临时字符串token中
token += ch;
if (ch == " " || p == (exp.Length - 1)) {
//计算符号后面是有空格的, 此时token还没有内容, 如果不判断, 就会在这时出错
if (IsNumeric(token)) {
N.Push(int.Parse(token));
token = "";
}
}
else if (ch == "+" || ch == "-" || ch == "*" || ch == "/")
//如果不是数字, 并且是加减乘除某个操作符号, 压入符号栈
O.Push(ch);
if (N.Count == 2)
//数字栈有了两个数字后, 进行一次计算
Compute(N, O);
}
}
//计算两个数字结果的方法
static void Compute(Stack<int> N, Stack<string> O)
{
int oper1, oper2;
string oper;
oper2 = Convert.ToInt32(N.Pop());//第二个数后入栈, 在栈顶, 所以先出栈的是oper2
oper1 = Convert.ToInt32(N.Pop());//第一个数先入栈, 在栈底, 所以后出栈的是oper1
oper = Convert.ToString(O.Pop());
//按照加减乘除, 计算结果, 并将结果压入数字栈
switch (oper) {
case "+":
N.Push(oper1 + oper2);
break;
case "-":
N.Push(oper1 - oper2);
break;
case "*":
N.Push(oper1 * oper2);
break;
case "/":
N.Push(oper1 / oper2);
break;
}
}
}
}
代码运行结果 :
实际上用Stack 来执行后缀算术表达式的计算会更容易. 大家在练习里会有机会实现后缀算数计算器。
Peek 方法
Peek方法会让人们在不把数据项移出堆栈的情况下看到栈顶数据项的值. 如果没有这种方法, 那么就需要把数据项从堆栈内移除才会知道它的数值. 当大家想在栈顶数据项出栈之前查看它的数值的时候, 就可以采用这种方法 :
if (IsNumeric(Nums.Peek()))
num = Nums.Pop();:
Clear方法
Clear方法会把所有数据项从堆栈内移除. 很难说清楚Clear方法是否会影响堆栈的容量. 因为无法检查堆栈的实际容量, 所以最好的办法就是假设堆栈的容量被重新设置为初始默认的10 个元素的大小.
Clear方法的应用场景是在出现错误时清除堆栈数据. 例如, 在上述表达式求值器中, 如果遇到除以0 的操作, 这就是错误, 需要清除堆栈:
case "/":
if (oper2 == 0) {
Console.WriteLine("除零错误! 清除此前结果");
N.Clear();
}
else
N.Push(oper1 / oper2);
break;
Contains方法
Contains方法用来确定指定的元素是否在堆栈内. 如果找到该元素, 那么此方法会返回true;否则就返回false. 该方法可以用来寻找堆栈内非栈顶的数值. 比如检查是否存在某个会导致处理错误的字符:
if (myStack.Contains(" "))
//找到了空格
else
//没找到空格
CopyTo方法和ToArray 方法
CopyTo方法会把堆栈内的内容复制到一个数组中. 数组必须是 Object类型, 因为这是所有堆栈对象的数据类型. 此方法需要两个参数:一个数组和开始放置堆栈元素的数组的起始索引. 堆栈内元素按照LIFO的顺序进行复制操作, 就好像对它们进行出栈操作一样. 下面这段代码说明了CopyTo方法的调用:
static void Main()
{
Stack<object> myStack = new Stack<object>();
Console.WriteLine("从栈顶到栈底的数字依次是 :");
for (int i = 0; i < 10; i++) {
myStack.Push(i);
Console.Write($"{9 - i} ");
}
object[] myArray = new object[myStack.Count + 5];
for (int i = 0; i < myArray.Length; i++) {
myArray[i] = "空";
}
//第二个参数代表开始接受出栈数据的数组索引
//如果从该位置开始, 剩余数组长度不足以接受全部出栈数据, 就会报错
myStack.CopyTo(myArray, 3);
Console.WriteLine();
Console.WriteLine("从数组索引3位置开始接受CopyTo方法的出栈数据, 操作完成后数组内容如下 :");
for (int i = 0; i < myArray.Length; i++) {
Console.WriteLine($"元素{i}:{myArray[i]} ");
}
Console.ReadLine();
}
代码运行结果 :

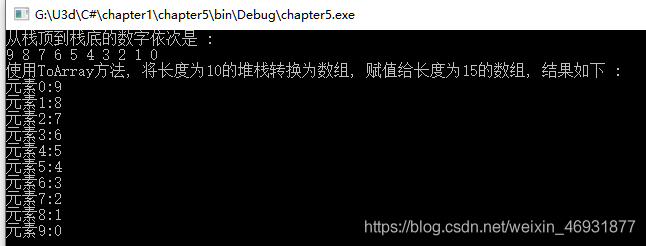
ToArray方法的工作原理与CopyTo方法类似. 但是用户无法指定数组的起始索引位置, 而是需要在赋值语句中创建新的数组. 实例如下所示:
static void Main()
{
Stack<object> myStack = new Stack<object>();
Console.WriteLine("从栈顶到栈底的数字依次是 :");
for (int i = 0; i < 10; i++) {
myStack.Push(i);
Console.Write($"{9 - i} ");
}
object[] myArray = new object[myStack.Count + 5];
for (int i = 0; i < myArray.Length; i++) {
myArray[i] = "空";
}
//使用ToArray方法返回的数组为myArray赋值后, 之前的赋值就都没意义了, 因为数组对象被直接替换了
//此处依然保留上方的赋值操作, 是为了对比打印结果更好的理解这里
myArray = myStack.ToArray();
Console.WriteLine();
Console.WriteLine("使用ToArray方法, 将长度为10的堆栈转换为数组, 赋值给长度为15的数组, 结果如下 :");
for (int i = 0; i < myArray.Length; i++) {
Console.WriteLine($"元素{i}:{myArray[i]} ");
}
Console.ReadLine();
}
Stack 类的实例:十进制向多种进制的转换
虽然在大多数商务应用中都采用十进制数, 但是一些科学技术应用则要求把数字表示成其他进制形式. 许多计算机系统应用程序要求数字既可以表示成八进制形式, 也可以表示成二进制形式.
把十进制数转化为八进制或二进制数的算法之一是利用堆栈来实现的. 下面列出了该算法的步骤:(原书这一段直译意思不清, 所以译者进行的补充说明. )
- 假设要进行转换的十进制数字是N
- 假设要转换为X进制数
- N/X的余数压入堆栈
- N/X的商, 转换为整型, 再赋值给N
- 循环重复步骤3和步骤4, 直到N变成0
以上算法过程结束后, 将堆栈中的数字依次出栈就得到了十进制N对应的X进制数字, 以下是代码实现 :
static void Main()
{
while (true) {
int num, baseNum;
Console.Write("输入一个十进制数字 :");
num = int.Parse(Console.ReadLine());
Console.Write("输入代表目标进制的数字 : ");
//应该输入大于1小于10的数字, 1进制没有意义报错,
//而如果大于10进制, 还需要额外处理大于10的单个数字的符号, 有兴趣的可以自己实现
baseNum = int.Parse(Console.ReadLine());
Console.Write($"{num}转换为{baseNum}进制后是 : ");
MulBase(num, baseNum);
Console.WriteLine("\n");
}
}
//进制转换函数
static void MulBase(int n, int b)
{
Stack<int> Digits = new Stack<int>();
do {
//余数入栈
Digits.Push(n % b);
//n和b都是整数, 相除结果的小数部分会被舍弃
n /= b;
} while (n != 0);
while (Digits.Count > 0)
Console.Write(Digits.Pop());
}
运行结果如下 :

上述程序说明了为什么堆栈对许多计算问题而言是一种有用的数据结构. 当把十进制数转化成其他进制的时候, 会从最右侧的数字开始操作, 并且按照这种工作方式一直到左侧. 在操作顺利执行的同时把每一个数字压入堆栈, 这是因为在操作结束的时候, 被转换的数字可以按照正确的顺序排列.
尽管堆栈是一种有用的数据结构, 但是一些应用程序为了更适合的其他目的而采用了基于列表的数据结构. 例如, 在杂货店或本地影碟租借店内顾客排的队伍. 不同于后进先出的堆栈, 在这些队伍内的第一个人应该最先出去(FIFO). 另外一个实例就是发送给网络(或本地)打印机的打印任务列表. 打印机应该首先处理最先发送的任务. 这些情况换做计算机来模拟的话, 都采用了一种基于列表的数据结构. 这种结构被称为是队列. 它是下一小节要讨论的主题。
队列, Queue类及其实现
队列是一种把数据从表的末端放入并在表的前端移除的数据结构. 队列会按照数据项出现的顺序来存储它们. 队列是先进先出(FIFO)数据结构的实例. 队列用来对提交的任务进行排序, 比如模拟用户等待的排队情况。
队列的操作
队列包含两种主要的操作. 一个是给队列添加新的数据项, 另一个则是把数据项从队列中移除. 添加新数据项的操作被称为是 Enqueue, 而从队列中移除数据项的操作则被称为是Dequeue. Enqueue操作会在队列的末尾添加一个数据项, 而Dequeue操作则会从队列的开始处移除一个数据项. 图5-2 就举例说明了这些操作。

队列的另外一个主要操作就是查看起始数据项. 像Stack 类一样使用名为Peek的方法查看起始的数据项. 这种方法仅仅返回数据项, 而不会把数据项从队列中移除。
Queue类的其他的属性也会对编程有所帮助. 然而, 在讨论这些属性之前, 还是先来看看如何能实现一个Queue类。
Queue的实现
就像前面的自定义堆栈类CStack一样, 由于数据的数量是不确定的, 自定义的Queue类也要借助ArrayList来存储数据.
当需要往队列中插入数据项时, ArrayList的Add方法会把数据项新增在末尾. 当需要从队列中移除数据项时, 使用ArrayList的RemoveAt方法移除第一个元素.
我们自己实现的队列类CQueue包含EnQueue方法、DeQueue方法、ClearQueue方法、Peek方法以及Count方法, 而且还有一个用于此类的默认构造函数:
public class CQueue
{
private ArrayList pqueue;
public CQueue()
{
pqueue = new ArrayList();
}
public void EnQueue(object item)
{
pqueue.Add(item);
}
public void DeQueue()
{
pqueue.RemoveAt(0);
}
public object Peek()
{
return pqueue[0];
}
public void ClearQueue()
{
pqueue.Clear();
}
public int Count()
{
return pqueue.Count;
}
}
Queue类:实例应用
前面已经提到了用于Queue类的主要方法, 而且还了解了这些方法在Queue类中的实现.
下面通过查看一个用Queue作为基本数据结构的实际编程问题来进一步讨论这些方法. 首先需要说明一下Queue对象的几个基本属性.
在对一个新的Queue对象实例化的时候, 队列默认的容量是32个, 当队列已满时, 其容量会双倍增长. 这就意味着当队列最初达到满容量时, 其新的容量值会变为64个. 但是大家可以不用受这些数值的限制. 在实例化对队列时, 大家可以指定一个不同的初始容量值. 如下所示:
//忘了说明一点, 这一章书中源代码的堆栈与队列的实例化, 作者都使用的非泛型方式
//如果你看到了泛型方式的实例化, 说明是我重写过的
//对于本书要说明的数据结构和算法知识来说, 选择哪个方式并无影响
//不过微软官方不推荐非泛型方式
Queue myQueue = new Queue(100);
这个设置把队列的容量值设为了100 个数据项. 当然, 大家也可以通过改变构造函数的参数来改变队列扩容时会增长的数量 :
Queue myQueue = new Queue(32, 3);
泛型Queue初始化如下所示:
Queue<int> numbers = new Queue<int>();
This line specifies a growth rate of 3 with the default initial capacity. You have to specify the capacity even if it’s the same as the default capacity since the constructor is looking for a method with a different signature.
(以上原文与前面描述的内容, 一半自相矛盾, 一半不知所云, 不予翻译了, 有兴趣的自行翻译, 不过就算跳过也不影响学习后面内容, 可以选择无视)
队列经常用来模拟人们排队的情况. 比如在单身舞会上. 男士们和女士们进入会场并且站成两队.
舞池很小, 只能同时容纳三对男女跳舞, 当舞池中有空间时, 就在队列中寻找最靠前的一位男士以及最靠前的一位女士入场. 一旦有一对舞者离开舞池, 则按照这个规则继续在队列中挑选下一对男女入场. 如果队伍中无法凑成一对男女舞者了, 则将这一信息显示出来, 以寻求其他舞伴.
我们将用Struct类型表示每一位舞者, 其中包含两个String类方法(Chars方法和Substring方法)用来构建舞者. 下面就是这段程序:
using System;
using System.Collections.Generic;
//存储舞者数据的结构类型, 实际性别属性在逻辑中没用到
public struct Dancer {
//舞者姓名
public string name;
//舞者性别
public string sex;
}
class Class1 {
static void Main(string[] args)
{
//男性队列
Queue<Dancer> males = new Queue<Dancer>();
//女性队列
Queue<Dancer> females = new Queue<Dancer>();
//初始化测试数据
formLines(males, females);
//初始有两对舞者, 还能进一对
startDancing(males, females);
//下一对儿舞者准备
headOfLine(males, females);
//从队列中选择下一对舞者结成队伍
newDancers(males, females);
//下一对儿舞者准备
headOfLine(males, females);
//从队列中选择下一对舞者出来结成队伍
newDancers(males, females);
Console.Read();
}
static void headOfLine(Queue<Dancer> male, Queue<Dancer> female)
{
if (male.Count > 0 && female.Count > 0){
Console.WriteLine($"请 : {male.Peek().name} 和 {female.Peek().name}准备入场");
}
else if (male.Count > 0)
Console.WriteLine("下一位男士是: " + male.Peek().name);
else
Console.WriteLine("下一位女士是: " + female.Peek().name);
Console.WriteLine();
}
static void newDancers(Queue<Dancer> male, Queue<Dancer> female)
{
if (male.Count > 0 && female.Count > 0) {
male.Dequeue();
female.Dequeue();
}
else if ((male.Count > 0) && (female.Count == 0))
Console.WriteLine("缺少一位女士舞伴");
else if ((female.Count > 0) && (male.Count == 0))
Console.WriteLine("缺少一位男士舞伴");
}
static void startDancing(Queue<Dancer> male, Queue<Dancer> female)
{
Console.WriteLine("现在舞池中的舞者是 : ");
Console.WriteLine();
for (int count = 0; count < 2; count++) {
Console.WriteLine($"{male.Dequeue().name} 和 {female.Dequeue().name}");
}
}
//设置两个队列的测试数据
static void formLines(Queue<Dancer> male, Queue<Dancer> female)
{
//原文读取的一个本地文件加载的数据, 我给改成在程序内设置简单的测试数据了
//为了测试, 故意让男士少一位
Dancer d = new Dancer();
for (int i = 0; i <4; i++) {
if (i<3) {
d.sex = "男士";
d.name = $"英俊小伙{male.Count + 1}";
male.Enqueue(d);
}
d.sex = "女士";
d.name = $"靓丽姑娘{female.Count + 1}";
female.Enqueue(d);
}
}
}
用队列存储数据
队列的另外一种用途是存储数据. 回顾计算机的早期时代, 那时的程序都是通过穿孔卡片录入到大型计算机内, 其中每张卡片上存有单独一条程序语句. 卡片用机械排序器进行存储, 这种排序器采用了类似箱子的结构. 这里可以用队列存储数据的方式来模拟此过程. 这种排序方法被称为是基数排序. 基数排序在编程的指令系统中不是最快的排序方法, 但是它却能说明队列在这方面的有趣用法.
基数排序是通过对一组数据进行两遍排序来操作的. 在这种情况下, 整数的取值范围是从0到99. 第一遍是基于个位上的数字进行排序, 而第二遍则是基于十位上的数字进行排序.根据这些位置上的每个数字来把每一个数放置在一个"箱子"内. 假设有下列这些数:
91、46、85、15、92、35、31、22
第一遍按照个位数排序的结果是:
• 0 号箱子:
• 1 号箱子:91 31
• 2 号箱子:92 22
• 3 号箱子:
• 4 号箱子:
• 5 号箱子:85 15 35
• 6 号箱子:46
• 7 号箱子:
• 8 号箱子:
• 9 号箱子:
现在, 把这些数按照它们在箱子中的位置排列起来, 结果如下所示:
91、31、92、22、85、15、35、46
接下来, 取上述列表, 按照十位上的数字对这些数排序后放入适当的箱子内:
0 号箱子:
1 号箱子:15
2 号箱子:22
3 号箱子:31 35
4 号箱子:46
5 号箱子:
6 号箱子:
7 号箱子:
8 号箱子:85
9 号箱子:91 92
把这些数从箱子内取出, 并且把它们放回到列表内. 此时就是这组整数排序后的结果:
15、22、31、35、46、85、91、92
用队列来表示这些箱子就可以实现这个算法. 针对每一位数字一共需要九个队列. 用取余运算和整除运算就可以确定个位上的数字以及十位上的数字. 剩下的事情就是把数添加到适当的队列内, 接着根据个位上的数字再把数从队列中取出进行重新排序, 随后根据十位上的数字重复上述操作. 最后的结果就是排序后的整数列表.
利用队列实现基数排序的代码如下:
using System;
using System.Collections.Generic;
class Class1 {
//代表基数的枚举
enum DigitType {
ones = 1, tens = 10 }
//显示指定数组内容
static void DisplayArray(int[] n)
{
for (int x = 0; x <= n.GetUpperBound(0); x++)
Console.Write(n[x] + " ");
}
//按照指定的基数将指定数组的元素放入与基数数字对应的队列中
static void RSort(Queue<int>[] que, int[] n, DigitType digit)
{
int snum;
for (int x = 0; x <= n.GetUpperBound(0); x++) {
if (digit == DigitType.ones)
snum = n[x] % 10;
else
snum = n[x] / 10;
que[snum].Enqueue(n[x]);
}
}
//从指定的队列数组中将每个队列的数字依次取出, 放入同一个整数数组中
static void BuildArray(Queue<int>[] que, int[] n)
{
int y = 0;
for (int x = 0; x <= 9; x++)
while (que[x].Count > 0) {
n[y] = que[x].Dequeue();
y++;
}
}
static void Main(string[] args)
{
Queue<int>[] numQueue = new Queue<int>[10];
Random rnd = new Random();
int[] nums = new int[10];
for (int i = 0; i < nums.Length; i++) {
nums[i] = rnd.Next(100);
}
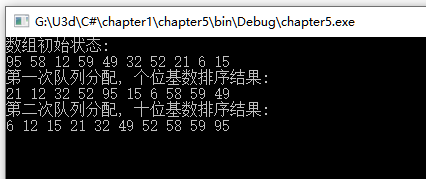
Console.WriteLine("数组初始状态: ");
DisplayArray(nums);
for (int i = 0; i < 10; i++)
numQueue[i] = new Queue<int>();
RSort(numQueue, nums, DigitType.ones);
BuildArray(numQueue, nums);
Console.WriteLine();
Console.WriteLine("第一次队列分配, 个位基数排序结果: ");
DisplayArray(nums);
RSort(numQueue, nums, DigitType.tens);
BuildArray(numQueue, nums);
Console.WriteLine();
Console.WriteLine("第二次队列分配, 十位基数排序结果: ");
DisplayArray(nums);
Console.Read();
}
}
代码运行结果如下 :
用RSort方法的参数包括一个队列数组、一个整数数组以及一个枚举值. 此枚举值代表要对个位上的数字还是对十位上的数字进行排序. 如果是个位, 那么排序的数字就是这个整数对10 进行取模运算后的余数. 如果是十位, 那么排序的数字则是对这个整数除以10后商的整数部分.
为了将排序结果重新构建为一个数组, 当只要队列中有数据, 就连续的Dequeue操作直到队列数组中的每个队列都为空. 这个操作在BuildArray子程序中执行, 这个过程是从保存较小数字的队列开始的, 所以最终得到的整数数组是有序的.
源自Queue类的优先队列
正如之前所说, 队列是一种先进先出的数据结构. 然而, 对于一些程序而言, 需要一种可以把具有最高优先级的数据项最先移除的数据结构, 即使这个数据项在结构中不是“最早进入的”一个. 对于这类程序, 有一种特殊的队列, 那就是优先队列.
许多程序在操作中都利用到了优先队列. 一个很好的实例就是在计算机操作系统内的进程处理. 某些进程可能有高于其他进程的优先级. 进程通常会根据优先级进行编号, 优先级为0 的进程比优先级为20的任务具有更高的优先性.
通常会把存储在优先队列中的数据项作为键值对来构造, 其中键就是指优先级, 而值则代表数据本身. 例如, 可以按照如下形式对一个操作系统进程进行定义:
struct Process
{
//优先级
int priority;
//进程名称
string name;
}
默认的Queue对象无法用作优先队列. DeQueue方法在被调用时只会把队列中的第一个数据项移除. 但是, 可以从 Queue类派生出自己的优先队列类, 同时覆盖DeQueue方法来实现自己的需求.
把这个自定义的队列类称为PQueue. 所有Queue的方法都可以照常使用, 同时覆盖Dequeue方法来移除具有最高优先级的数据项. 为了不从队列前端移除数据项, 首先需要把队列的数据项写入一个数组. 然后遍历整个数组从而找到具有最高优先级的数据项. 最后, 根据标记的数据项, 就可以在不考虑此标记数据项的同时对队列进行重新构建.
下面就是有关PQueue类的代码:
using System.Collections;
public struct pqItem {
public int priority;
public string name;
public pqItem(int p, string n)
{
priority = p;
name = n;
}
}
//非泛型的Queue才提供了可继承的各种虚方法
public class PQueue : Queue {
public override object Dequeue()
{
object[] items;
//将当队列的数据转换为数组
items = this.ToArray();
//标记优先级值最低, 也就是优先级级别最高的数组元素索引
int minPriorityIndex;
//初始假定索引0的元素优先级最高
minPriorityIndex = 0;
for (int i = 1; i <= items.GetUpperBound(0); i++) {
//每次找到priority更小的元素, 都将更新标记最高优先级元素的索引
if (((pqItem)items[i]).priority < ((pqItem)items[minPriorityIndex]).priority) {
minPriorityIndex = i;
}
}
//清空队列的数据
this.Clear();
//使用之前转换的数组数据重新填充队列
for (int i = 0; i <= items.GetUpperBound(0); i++) {
//最高优先级, 也就是priority值最小的元素, 不加入队列, 它已经被Dequeue了
if (i != minPriorityIndex) {
this.Enqueue(items[i]);
}
}
//返回被优先Dequeue的数据
return items[minPriorityIndex];
}
}
(使用下述代码测试下优先队列的效果
static void Main(string[] args)
{
PQueue pq = new PQueue();
Random rnd = new Random(1);
int temp = 0;
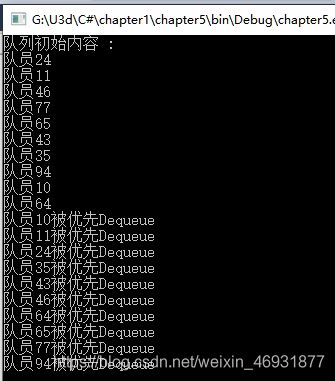
Console.WriteLine("队列初始内容 :");
for (int i = 0; i < 10; i++) {
temp = rnd.Next(100);
pq.Enqueue(new pqItem(temp, $"队员{temp.ToString()}"));
Console.WriteLine($"队员{temp.ToString()}");
}
//Dequeue所有数据项, 观察顺序
while (pq.Count > 0) {
Console.WriteLine(((pqItem)pq.Dequeue()).name + "被优先Dequeue");
}
Console.ReadLine();
}
运行结果如下 :
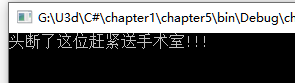
接下来的代码说明了PQueue类的一个简单应用. 急诊等待室对就诊的病人配置了优先级.
病情更严重的病人应该在其他病人之前进行治疗. 下面这个程序模拟了三位几乎在同一时间进入急诊室的病人. 分诊护士在检查完每一位病人后会分配得他们一个优先级, 同时会把这些病人添加到队列内. 进行治疗的第一个病人会通过Dequeue方法从队列中移除。
static void Main()
{
PQueue erwait = new PQueue();
pqItem[] erPatient = new pqItem[4];
pqItem nextPatient;
erPatient[0].name = "头发干枯分叉这位";
erPatient[0].priority = 1;
erPatient[1].name = "头断了这位";
erPatient[1].priority = 0;//优先级数最低, 表示优先级最高
erPatient[2].name = "吃饭咽着这位";
erPatient[2].priority = 3;
for (int x = 0; x <= erPatient.GetUpperBound(0); x++)
erwait.Enqueue(erPatient[x]);
nextPatient = (pqItem)erwait.Dequeue();
Console.WriteLine($"{nextPatient.name}赶紧送手术室!!!");
Console.ReadLine();
}