深蓝学院-多传感器融合定位-第5章作业
深蓝学院-多传感器融合定位-第5章作业
- 第一题:不基于转台的加速度计标定:Jacobian推导
- 第二题:完成标定(自动求导)
- 第三题:完成标定(解析式求导)
-
- 1. 标量对向量求导法
- 2. 向量对向量求导法
Github: https://github.com/WeihengXia0123/LiDar-SLAM
第一题:不基于转台的加速度计标定:Jacobian推导
首先,我们计算出向量 a \textbf{a} a的表达:
a = ( I − S a ) K a ′ A − b a = [ 1 0 0 − S a y x 1 0 − S a z x − S a z y 1 ] [ K a x − 1 0 0 0 K a y − 1 0 0 0 K a z − 1 ] [ A x A y A z ] − [ b a x b a y b a z ] = . . . ( 老 衲 掐 指 一 算 ) = [ K a x − 1 A x − b a x − S a y x K a x − 1 A x + K a y − 1 A y − b a y − S a y x K a x − 1 A x − S a z y K a y − 1 A y + K a z − 1 A z − b a z ] \begin{aligned} \textbf{a} &= (I-S_a)K'_aA-b_a \\ &= \left[ \begin{matrix} 1 & 0 & 0 \\ -S_{ayx} & 1 & 0 \\ -S_{azx} & -S_{azy} & 1 \end{matrix} \right] \left[ \begin{matrix} K_{ax}^{-1} & 0 & 0 \\ 0 & K_{ay}^{-1} & 0 \\ 0 & 0 & K_{az}^{-1} \end{matrix} \right] \left[ \begin{matrix} A_x\\ A_y\\ A_z \end{matrix} \right] - \left[ \begin{matrix} b_{ax}\\ b_{ay}\\ b_{az} \end{matrix} \right] \\\\ &= ...(老衲掐指一算)\\ \\ &= \left[ \begin{matrix} K_{ax}^{-1}A_x-b_{ax} \\ -S_{ayx}K_{ax}^{-1}A_x+K_{ay}^{-1}A_y-b_{ay} \\ -S_{ayx}K_{ax}^{-1}A_x-S_{azy}K_{ay}^{-1}A_y+K_{az}^{-1}A_z-b_{az} \end{matrix} \right] \end{aligned} a=(I−Sa)Ka′A−ba=⎣⎡1−Sayx−Sazx01−Sazy001⎦⎤⎣⎡Kax−1000Kay−1000Kaz−1⎦⎤⎣⎡AxAyAz⎦⎤−⎣⎡baxbaybaz⎦⎤=...(老衲掐指一算)=⎣⎡Kax−1Ax−bax−SayxKax−1Ax+Kay−1Ay−bay−SayxKax−1Ax−SazyKay−1Ay+Kaz−1Az−baz⎦⎤
其次,基于上面的结果,咱们就可以计算残差Residual了:
f ( θ a c c ) = ∣ ∣ g ∣ ∣ 2 − ∣ ∣ a ∣ ∣ 2 = g 0 2 − a T a = g 0 2 − ( K a x − 1 A x − b a x ) 2 − ( − S a y x K a x − 1 A x + K a y − 1 A y − b a y ) 2 − ( − S a z x K a x − 1 A x − S a z y K a y − 1 A y + K a z − 1 A z − b a z ) 2 \begin{aligned} f(\theta^{acc}) &= ||g||^2-||a||^2\\ &= g_{0}^{2} - a^Ta\\ &= g_{0}^2 - (K_{ax}^{-1}A_x-b_{ax})^2 - (-S_{ayx}K_{ax}^{-1}A_x+K_{ay}^{-1}A_y-b_{ay})^2\\ &\ \ \ \ -(-S_{azx}K_{ax}^{-1}A_x-S_{azy}K_{ay}^{-1}A_y+K_{az}^{-1}A_z-b_{az})^2 \end{aligned} f(θacc)=∣∣g∣∣2−∣∣a∣∣2=g02−aTa=g02−(Kax−1Ax−bax)2−(−SayxKax−1Ax+Kay−1Ay−bay)2 −(−SazxKax−1Ax−SazyKay−1Ay+Kaz−1Az−baz)2
好了,有了 f ( ⋅ ) f(\cdot) f(⋅)的完整表达形式,咱们就可以计算Jacobian了:


这里因为Residual只有一个 f f f,所以 J ( θ a c c ) J(\theta^{acc}) J(θacc)是一个1x9的向量。
通过复合函数的链式求导法则和上面求得的 f f f,可以得到:
J 1 = ∂ f ∂ S a y x = − 2 ( − S a y x K a x − 1 A x + K a y − 1 A y − b a y ) ( − K a x − 1 A x ) J 2 = ∂ f ∂ S a z x = − 2 ( − S a z x K a x − 1 A x − S a z y K a y − 1 A y + K a z − 1 A z − b a z ) ( − K a x − 1 A x ) J 3 = ∂ f ∂ S a z y = − 2 ( − S a z x K a x − 1 A x − S a z y K a y − 1 A y + K a z − 1 A z − b a z ) ( − K a y − 1 A y ) J 4 = ∂ f ∂ K a x = − 2 ( K a x − 1 A x − b a x ) ( − K a x − 2 A x ) − 2 ( − S a y x K a x − 1 A x + K a y − 1 A y − b a y ) ( S a y x K a x − 2 A x ) − 2 ( − S a z x K a x − 1 A x − S a z y K a y − 1 A y + K a z − 1 A z − b a z ) ( S a z x K a x − 2 A x ) J 5 = ∂ f ∂ K a y = − 2 ( − S a y x K a x − 1 A x + K a y − 1 A y − b a y ) ( − K a y − 2 A y ) − 2 ( − S a z x K a x − 1 A x − S a z y K a y − 1 A y + K a z − 1 A z − b a z ) ( S a z y K a y − 2 A y ) J 6 = ∂ f ∂ K a z = − 2 ( − S a z x K a x − 1 A x − S a z y K a y − 1 A y + K a z − 1 A z − b a z ) ( − K a z − 2 A z ) J 7 = ∂ f ∂ b a x = 2 ( K a x − 1 A x − b a x ) J 8 = ∂ f ∂ b a y = 2 ( − S a y x K a x − 1 A x + K a y − 1 A y − b a y ) J 9 = ∂ f ∂ b a y = 2 ( − S a z x K a x − 1 A x − S a z y K a y − 1 A y + K a z − 1 A z − b a z ) \begin{aligned} J_1 &= \frac{\partial f}{\partial S_{ayx}} = -2(-S_{ayx}K_{ax}^{-1}A_x+K_{ay}^{-1}A_y-b_{ay})(-K_{ax}^{-1}A_x) \\ J_2 &= \frac{\partial f}{\partial S_{azx}} = -2(-S_{azx}K_{ax}^{-1}A_x-S_{azy}K_{ay}^{-1}A_y+K_{az}^{-1}A_z-b_{az})(-K_{ax}^{-1}A_x)\\ J_3 &= \frac{\partial f}{\partial S_{azy}} = -2(-S_{azx}K_{ax}^{-1}A_x-S_{azy}K_{ay}^{-1}A_y+K_{az}^{-1}A_z-b_{az})(-K_{ay}^{-1}A_y)\\ J_4 &= \frac{\partial f}{\partial K_{ax}} = -2(K_{ax}^{-1}A_x-b_{ax})(-K_{ax}^{-2}A_x) \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ -2(-S_{ayx}K_{ax}^{-1}A_x+K_{ay}^{-1}A_y-b_{ay})(S_{ayx}K_{ax}^{-2}A_x) \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ -2(-S_{azx}K_{ax}^{-1}A_x-S_{azy}K_{ay}^{-1}A_y+K_{az}^{-1}A_z-b_{az})(S_{azx}K_{ax}^{-2}A_x) \\ J_5 &= \frac{\partial f}{\partial K_{ay}} = -2(-S_{ayx}K_{ax}^{-1}A_x+K_{ay}^{-1}A_y-b_{ay})(-K_{ay}^{-2}A_y)\\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ -2(-S_{azx}K_{ax}^{-1}A_x-S_{azy}K_{ay}^{-1}A_y+K_{az}^{-1}A_z-b_{az})(S_{azy}K_{ay}^{-2}A_y) \\ J_6 &= \frac{\partial f}{\partial K_{az}} = -2(-S_{azx}K_{ax}^{-1}A_x-S_{azy}K_{ay}^{-1}A_y+K_{az}^{-1}A_z-b_{az})(-K_{az}^{-2}A_z)\\ J_7 &= \frac{\partial f}{\partial b_{ax}} = 2(K_{ax}^{-1}A_x-b_{ax})\\ J_8 &= \frac{\partial f}{\partial b_{ay}} = 2(-S_{ayx}K_{ax}^{-1}A_x+K_{ay}^{-1}A_y-b_{ay})\\ J_9 &= \frac{\partial f}{\partial b_{ay}} = 2(-S_{azx}K_{ax}^{-1}A_x-S_{azy}K_{ay}^{-1}A_y+K_{az}^{-1}A_z-b_{az})\\ \end{aligned} J1J2J3J4J5J6J7J8J9=∂Sayx∂f=−2(−SayxKax−1Ax+Kay−1Ay−bay)(−Kax−1Ax)=∂Sazx∂f=−2(−SazxKax−1Ax−SazyKay−1Ay+Kaz−1Az−baz)(−Kax−1Ax)=∂Sazy∂f=−2(−SazxKax−1Ax−SazyKay−1Ay+Kaz−1Az−baz)(−Kay−1Ay)=∂Kax∂f=−2(Kax−1Ax−bax)(−Kax−2Ax) −2(−SayxKax−1Ax+Kay−1Ay−bay)(SayxKax−2Ax) −2(−SazxKax−1Ax−SazyKay−1Ay+Kaz−1Az−baz)(SazxKax−2Ax)=∂Kay∂f=−2(−SayxKax−1Ax+Kay−1Ay−bay)(−Kay−2Ay) −2(−SazxKax−1Ax−SazyKay−1Ay+Kaz−1Az−baz)(SazyKay−2Ay)=∂Kaz∂f=−2(−SazxKax−1Ax−SazyKay−1Ay+Kaz−1Az−baz)(−Kaz−2Az)=∂bax∂f=2(Kax−1Ax−bax)=∂bay∂f=2(−SayxKax−1Ax+Kay−1Ay−bay)=∂bay∂f=2(−SazxKax−1Ax−SazyKay−1Ay+Kaz−1Az−baz)
第二题:完成标定(自动求导)
一开始改错地方了,直接把人家定义的mis_mat改了:
CalibratedTriad_( const _T &mis_yz = _T(0), const _T &mis_zy = _T(0), const _T &mis_zx = _T(0),
const _T &mis_xz = _T(0), const _T &mis_xy = _T(0), const _T &mis_yx = _T(0),
const _T &s_x = _T(1), const _T &s_y = _T(1), const _T &s_z = _T(1),
const _T &b_x = _T(0), const _T &b_y = _T(0), const _T &b_z = _T(0) );
~CalibratedTriad_(){
};
inline _T misYZ() const {
return -mis_mat_(0,1); };
inline _T misZY() const {
return mis_mat_(0,2); };
inline _T misZX() const {
return -mis_mat_(1,2); };
inline _T misXZ() const {
return mis_mat_(1,0); };
inline _T misXY() const {
return -mis_mat_(2,0); };
inline _T misYX() const {
return mis_mat_(2,1); };
--------------------------------------------------------
// 我一开始把下面这个矩阵按课件改了....
mis_mat_ << _T(1) , -mis_yz , mis_zy ,
mis_xz , _T(1) , -mis_zx ,
-mis_xy , mis_yx , _T(1) ;
其实只需要修改三处TODO:
CalibratedTriad_<_T2> calib_triad(
//
// TODO: implement lower triad model here
//
// mis_yz, mis_zy, mis_zx:
_T2(0), _T2(0), _T2(0),
// mis_xz, mis_xy, mis_yx:
params[0], params[1], params[2],
// s_x, s_y, s_z:
params[3], params[4], params[5],
// b_x, b_y, b_z:
params[6], params[7], params[8]
);
------------------------------------------
//
// TODO: implement lower triad model here
//
acc_calib_params[0] = init_acc_calib_.misXZ();
acc_calib_params[1] = init_acc_calib_.misXY();
acc_calib_params[2] = init_acc_calib_.misYX();
------------------------------------------
acc_calib_ = CalibratedTriad_<_T>(
//
// TODO: implement lower triad model here
//
0,0,0,
min_cost_calib_params[0],
min_cost_calib_params[1],
min_cost_calib_params[2],
min_cost_calib_params[3],
min_cost_calib_params[4],
min_cost_calib_params[5],
min_cost_calib_params[6],
min_cost_calib_params[7],
min_cost_calib_params[8]
);
第三题:完成标定(解析式求导)
1. 标量对向量求导法
根据我第3章作业修改Ceres解析式的经验,这里直接改就行了(但要注意外部参数是用的template)。
原本的autodiff的struct如下,咱们要注意它的外部用了template :
template <typename _T1> struct MultiPosAccResidual
{
MultiPosAccResidual(
const _T1 &g_mag,
const Eigen::Matrix< _T1, 3 , 1> &sample
) : g_mag_(g_mag), sample_(sample){
}
template <typename _T2>
bool operator() ( const _T2* const params, _T2* residuals) const {
Eigen::Matrix<_T2, 3, 1> raw_samp(
_T2(sample_(0)),
_T2(sample_(1)),
_T2(sample_(2))
);
/* Apply undistortion transform to accel measurements
mis_mat_ << _T(1) , -mis_yz , mis_zy ,
mis_xz , _T(1) , -mis_zx ,
-mis_xy , mis_yx , _T(1) ;
scale_mat_ << s_x , _T(0) , _T(0) ,
_T(0) , s_y , _T(0) ,
_T(0) , _T(0) , s_z ;
bias_vec_ << b_x , b_y , b_z ;
define:
ms_mat_ = mis_mat_*scale_mat_
then the undistortion transform:
X' = T*K*(X - B)
can be implemented as:
unbias_data = ms_mat_*(raw_data - bias_vec_)
* assume body frame same as accelerometer frame,
* so bottom left params in the misalignment matris are set to zero */
CalibratedTriad_<_T2> calib_triad(
//
// TODO: implement lower triad model here
//
// mis_yz, mis_zy, mis_zx:
_T2(0), _T2(0), _T2(0),
// mis_xz, mis_xy, mis_yx:
params[0], params[1], params[2],
// s_x, s_y, s_z:
params[3], params[4], params[5],
// b_x, b_y, b_z:
params[6], params[7], params[8]
);
// apply undistortion transform:
Eigen::Matrix< _T2, 3 , 1> calib_samp = calib_triad.unbiasNormalize( raw_samp );
residuals[0] = _T2 (g_mag_) - calib_samp.norm();
return true;
}
static ceres::CostFunction* Create ( const _T1 &g_mag, const Eigen::Matrix< _T1, 3 , 1> &sample )
{
return ( new ceres::AutoDiffCostFunction< MultiPosAccResidual, 1, 9 > (
new MultiPosAccResidual<_T1>( g_mag, sample ) ) );
}
const _T1 g_mag_;
const Eigen::Matrix< _T1, 3 , 1> sample_;
};
看完上面autodiff的struct后,我们要改成解析式的class,而且还是模板class:
template <typename _T1>
class MultiPosAccResidual_Analytical : public ceres::SizedCostFunction<1, 9> {
public:
MultiPosAccResidual_Analytical(const _T1 &g_mag, const Eigen::Matrix< _T1, 3 , 1> &sample
) : g_mag_(g_mag), sample_(sample){
}
virtual bool Evaluate(double const* const* parameters,
double* residuals,
double** jacobians) const
{
Eigen::Matrix<double, 3, 1> raw_samp(
double(sample_(0)),
double(sample_(1)),
double(sample_(2))
);
/* Apply undistortion transform to accel measurements
mis_mat_ << _T(1) , -mis_yz , mis_zy ,
mis_xz , _T(1) , -mis_zx ,
-mis_xy , mis_yx , _T(1) ; */
CalibratedTriad_<double> calib_triad(
//
// TODO: implement lower triad model here
//
// mis_yz, mis_zy, mis_zx:
double(0), double(0), double(0),
// mis_xz, mis_xy, mis_yx:
parameters[0][0], parameters[0][1], parameters[0][2],
// s_x, s_y, s_z:
parameters[0][3], parameters[0][4], parameters[0][5],
// b_x, b_y, b_z:
parameters[0][6], parameters[0][7], parameters[0][8]
);
// apply undistortion transform:
Eigen::Matrix< double, 3 , 1> calib_samp = calib_triad.unbiasNormalize( raw_samp );
residuals[0] = g_mag_*g_mag_ - calib_samp.transpose()*calib_samp;
if(jacobians != NULL)
{
if(jacobians[0] != NULL)
{
double S1 = parameters[0][0];
double S2 = parameters[0][1];
double S3 = parameters[0][2];
double K1 = 1.0/parameters[0][3];
double K2 = 1.0/parameters[0][4];
double K3 = 1.0/parameters[0][5];
double b1 = parameters[0][6];
double b2 = parameters[0][7];
double b3 = parameters[0][8];
double A1 = sample_(0);
double A2 = sample_(1);
double A3 = sample_(2);
jacobians[0][0] = -2*(-S1*K1*A1 + K2*A2 - b2) * (-K1*A1);
jacobians[0][1] = -2*(-S2*K1*A1 - S3*K2*A2 + K3*A3 - b3) * (-K1*A1);
jacobians[0][2] = -2*(-S2*K1*A1 - S3*K2*A2 + K3*A3 - b3) * (-K2*A2);
jacobians[0][3] = -2*( K1*A1 - b1) * (-K1*K1*A1) \
- 2*(-S1*K1*A1 + K2*A2 - b2)*(S1*K1*K1*A1) \
- 2*(-S2*K1*A1 - S3*K2*A2 + K3*A3 - b3)*(S2*K1*K1*A1);
jacobians[0][4] = -2*(-S1*K1*A1 + K2*A2 - b2)*(K1*K1*A1) \
- 2*(-S2*K1*A1 - S3*K2*A2 + K3*A3 - b3)*(S3*K2*K2*A2);
jacobians[0][5] = -2*(-S2*K1*A1 - S3*K2*A2 + K3*A3 - b3)*(-K3*K3*A3);
jacobians[0][6] = 2*( K1*A1 - b1);
jacobians[0][7] = 2*(-S1*K1*A1 + K2*A2 - b2);
jacobians[0][8] = 2*(-S2*K1*A1 - S3*K2*A2 + K3*A3 - b3);
}
}
return true;
}
protected:
const _T1 g_mag_;
const Eigen::Matrix< _T1, 3 , 1> sample_;
};
**********************************
//最后记得调用这个class
**********************************
ceres::Problem problem;
for( int i = 0; i < static_samples.size(); i++)
{
// ceres::CostFunction* cost_function = MultiPosAccResidual<_T>::Create (
// g_mag_, static_samples[i].data()
// );
ceres::CostFunction *cost_function = new MultiPosAccResidual_Analytical<_T>(g_mag_, static_samples[i].data());
problem.AddResidualBlock (
cost_function, /* error fuction */
NULL, /* squared loss */
acc_calib_params.data() /* accel deterministic error params */
);
}
ceres::Solver::Options options;
options.linear_solver_type = ceres::DENSE_QR;
options.minimizer_progress_to_stdout = verbose_output_;
ceres::Solver::Summary summary;
ceres::Solve ( options, &problem, &summary );
if( summary.final_cost < min_cost)
{
min_cost = summary.final_cost;
min_cost_th = th_mult;
min_cost_static_intervals_ = static_intervals;
min_cost_calib_params = acc_calib_params;
}
cout << "residual " << summary.final_cost << endl;
坑点:
- 自动求导struct里面的
param[0] param[1] param[2] ...,但是解析式求导里面药用parameters[0][0] parameters[0][1] parameters[0][2] ...。我之前直接就用了个parameters[7],结果各种报错。- 这句Residual的很关键,因为原来的residual是没有平方的:
residuals[0] = g_mag_*g_mag_ - calib_samp.transpose()*calib_samp;
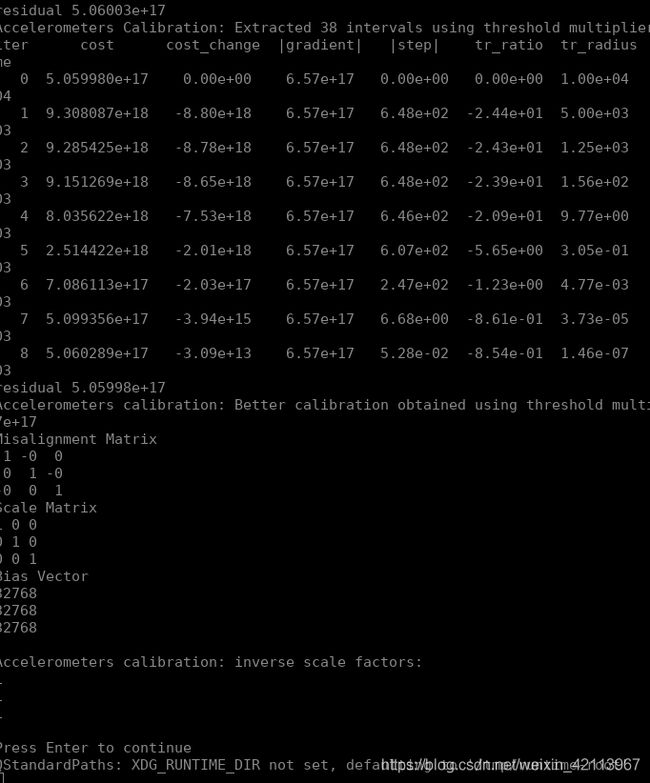
结果有点不如人意,尤其是scale差了500倍:
经过和群里的同学们讨论,估计问题出在化简的公式对初值很敏感,因为一开始那不是一个小量,但被我们忽略了:
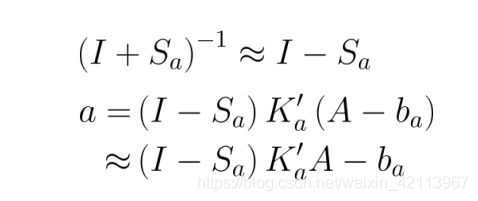
所以改用完整版的来:
a = ( I − S a ) K a ′ ( A − b a ) a = (I-S_a)K_a^{'}(A-b_a) a=(I−Sa)Ka′(A−ba)
由于我代码前面封装的好,直接删除之前所有的b项,然后把A改成(A-b)就搞定了:
double A1 = sample_(0)-b1;
double A2 = sample_(1)-b2;
double A3 = sample_(2)-b3;
jacobians[0][0] = -2*(-S1*K1*A1 + K2*A2 ) * (-K1*A1);
jacobians[0][1] = -2*(-S2*K1*A1 - S3*K2*A2 + K3*A3 ) * (-K1*A1);
jacobians[0][2] = -2*(-S2*K1*A1 - S3*K2*A2 + K3*A3 ) * (-K2*A2);
jacobians[0][3] = -2*( K1*A1 ) * (-K1*K1*A1) \
- 2*(-S1*K1*A1 + K2*A2)*(S1*K1*K1*A1) \
- 2*(-S2*K1*A1 - S3*K2*A2 + K3*A3)*(S2*K1*K1*A1);
jacobians[0][4] = -2*(-S1*K1*A1 + K2*A2)*(K1*K1*A1) \
- 2*(-S2*K1*A1 - S3*K2*A2 + K3*A3)*(S3*K2*K2*A2);
jacobians[0][5] = -2*(-S2*K1*A1 - S3*K2*A2 + K3*A3)*(-K3*K3*A3);
f ( θ a c c ) = ∣ ∣ g ∣ ∣ 2 − ∣ ∣ a ∣ ∣ 2 = g 0 2 − a T a = g 0 2 − ( K a x − 1 ( A x − b a x ) ) 2 − ( − S a y x K a x − 1 ( A x − b a x ) + K a y − 1 ( A y − b a y ) ) 2 − ( − S a z x K a x − 1 ( A x − b a x ) − S a z y K a y − 1 ( A y − b a y ) + K a z − 1 ( A z − b a z ) ) 2 \begin{aligned} f(\theta^{acc}) &= ||g||^2-||a||^2\\ &= g_{0}^{2} - a^Ta\\ &= g_{0}^2 - (K_{ax}^{-1}(A_x-b_{ax}))^2 - (-S_{ayx}K_{ax}^{-1}(A_x-b_{ax})+K_{ay}^{-1}(A_y-b_{ay}))^2\\ &\ \ \ \ -(-S_{azx}K_{ax}^{-1}(A_x-b_{ax})-S_{azy}K_{ay}^{-1}(A_y-b_{ay})+K_{az}^{-1}(A_z-b_{az}))^2 \end{aligned} f(θacc)=∣∣g∣∣2−∣∣a∣∣2=g02−aTa=g02−(Kax−1(Ax−bax))2−(−SayxKax−1(Ax−bax)+Kay−1(Ay−bay))2 −(−SazxKax−1(Ax−bax)−SazyKay−1(Ay−bay)+Kaz−1(Az−baz))2
J 7 = ∂ f ∂ b a x = 2 K a x − 1 ( K a x − 1 ( A x − b a x ) ) − 2 S a y x K a x − 1 ( − S a y x K a x − 1 ( A x − b a x ) + K a y − 1 ( A y − b a y ) ) − 2 S a z x K a x − 1 ( − S a z x K a x − 1 ( A x − b a x ) − S a z y K a y − 1 ( A y − b a y ) + K a z − 1 ( A z − b a z ) ) J 8 = ∂ f ∂ b a y = 2 K a y − 1 ( − S a y x K a x − 1 ( A x − b a x ) + K a y − 1 ( A y − b a y ) ) − 2 S a z y K a y − 1 ( − S a z x K a x − 1 ( A x − b a x ) − S a z y K a y − 1 ( A y − b a y ) + K a z − 1 ( A z − b a z ) ) J 9 = ∂ f ∂ b a y = 2 K a z − 1 ( − S a z x K a x − 1 ( A x − b a x ) − S a z y K a y − 1 ( A y − b a y ) + K a z − 1 ( A z − b a z ) ) \begin{aligned} J_7 &= \frac{\partial f}{\partial b_{ax}} = 2K_{ax}^{-1}(K_{ax}^{-1}(A_x-b_{ax}))-2S_{ayx}K_{ax}^{-1}(-S_{ayx}K_{ax}^{-1}(A_x-b_{ax})+K_{ay}^{-1}(A_y-b_{ay})) \\& \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ -2S_{azx}K_{ax}^{-1}(-S_{azx}K_{ax}^{-1}(A_x-b_{ax}) -S_{azy}K_{ay}^{-1}(A_y-b_{ay})+K_{az}^{-1}(A_z-b_{az}))\\ J_8 &= \frac{\partial f}{\partial b_{ay}} = 2K_{ay}^{-1}(-S_{ayx}K_{ax}^{-1}(A_x-b_{ax})+K_{ay}^{-1}(A_y-b_{ay})) \\& \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ -2S_{azy}K_{ay}^{-1}(-S_{azx}K_{ax}^{-1}(A_x-b_{ax}) -S_{azy}K_{ay}^{-1}(A_y-b_{ay})+K_{az}^{-1}(A_z-b_{az}))\\ J_9 &= \frac{\partial f}{\partial b_{ay}} = 2K_{az}^{-1}(-S_{azx}K_{ax}^{-1}(A_x-b_{ax}) -S_{azy}K_{ay}^{-1}(A_y-b_{ay})+K_{az}^{-1}(A_z-b_{az})) \end{aligned} J7J8J9=∂bax∂f=2Kax−1(Kax−1(Ax−bax))−2SayxKax−1(−SayxKax−1(Ax−bax)+Kay−1(Ay−bay)) −2SazxKax−1(−SazxKax−1(Ax−bax)−SazyKay−1(Ay−bay)+Kaz−1(Az−baz))=∂bay∂f=2Kay−1(−SayxKax−1(Ax−bax)+Kay−1(Ay−bay)) −2SazyKay−1(−SazxKax−1(Ax−bax)−SazyKay−1(Ay−bay)+Kaz−1(Az−baz))=∂bay∂f=2Kaz−1(−SazxKax−1(Ax−bax)−SazyKay−1(Ay−bay)+Kaz−1(Az−baz))
jacobians[0][6] = 2*K1*(K1*A1) - 2*S1*K1*(-S1*K1*A1+K2*A2) - 2*S2*K1*(-S2*K1*A1-S3*K2*A2+K3*A3);
jacobians[0][7] = 2*K2*(-S1*K1*A1+K2*A2) - 2*S3*K2*(-S2*K1*A1-S3*K2*A2+K3*A3);
jacobians[0][8] = 2*K3*(-S2*K1*A1-S3*K2*A2+K3*A3);
算出来结果完全不对了。。。还要debug下哪里写错了
2. 向量对向量求导法
小土豆:大师兄,为啥要改用这个方法呀!
大师兄:因为上面这种全部算出来再求导的方法太蠢了,老纳自己都不想再debug哪儿写错了还是哪儿程序打错了!
f ( θ a c c ) = ∣ ∣ g ∣ ∣ 2 − ∣ ∣ a ∣ ∣ 2 (1) \begin{aligned} \tag{1} f(\theta^{acc}) &= ||g||^2-||a||^2 \\ \\ \end{aligned} f(θacc)=∣∣g∣∣2−∣∣a∣∣2(1)
∂ f ( θ a c c ) ∂ θ a c c = − ∂ ∣ ∣ a ∣ ∣ 2 ∂ ∣ ∣ a ∣ ∣ ⋅ ∂ ∣ ∣ a ∣ ∣ ∂ a ⋅ ∂ a ∂ θ a c c = − 2 ∥ a ∥ ⋅ a ∥ a ∥ ⋅ ∂ a ∂ θ a c c (2) \begin{aligned} \tag{2} \frac{\partial{f(\theta^{acc})}}{\partial{\theta^{acc}}} &= - \frac{\partial{||a||^2}}{\partial{||a||}} \cdot \frac{\partial{||a||}}{\partial{a}} \cdot \frac{\partial{a}}{\partial{\theta^{acc}}}\\ &= -2\Vert a \Vert \cdot\frac{a}{\Vert a \Vert}\cdot \frac{\partial{a}}{\partial{\theta^{acc}}} \\ \end{aligned} ∂θacc∂f(θacc)=−∂∣∣a∣∣∂∣∣a∣∣2⋅∂a∂∣∣a∣∣⋅∂θacc∂a=−2∥a∥⋅∥a∥a⋅∂θacc∂a(2)
根据代码中对应的 a a a和 ∥ a ∥ \Vert a \Vert ∥a∥, 现在要计算 ∂ a ∂ θ a c c \frac{\partial{a}}{\partial{\theta^{acc}}} ∂θacc∂a:
代码实现:
template <typename _T1>
class MultiPosAccResidual_Analytical : public ceres::SizedCostFunction<1, 9> {
public:
MultiPosAccResidual_Analytical(const _T1 &g_mag, const Eigen::Matrix< _T1, 3 , 1> &sample
) : g_mag_(g_mag), sample_(sample){
}
virtual bool Evaluate(double const* const* parameters,
double* residuals,
double** jacobians) const
{
Eigen::Matrix<double, 3, 1> raw_samp(
double(sample_(0)),
double(sample_(1)),
double(sample_(2))
);
/* Apply undistortion transform to accel measurements
mis_mat_ << _T(1) , -mis_yz , mis_zy ,
mis_xz , _T(1) , -mis_zx ,
-mis_xy , mis_yx , _T(1) ; */
CalibratedTriad_<double> calib_triad(
//
// TODO: implement lower triad model here
//
// mis_yz, mis_zy, mis_zx:
double(0), double(0), double(0),
// mis_xz, mis_xy, mis_yx:
parameters[0][0], parameters[0][1], parameters[0][2],
// s_x, s_y, s_z:
parameters[0][3], parameters[0][4], parameters[0][5],
// b_x, b_y, b_z:
parameters[0][6], parameters[0][7], parameters[0][8]
);
// apply undistortion transform:
Eigen::Matrix< double, 3 , 1> calib_samp = calib_triad.unbiasNormalize( raw_samp );
// residuals[0] = g_mag_*g_mag_ - calib_samp.transpose()*calib_samp;
residuals[0] = g_mag_- calib_samp.norm();
if(jacobians != NULL)
{
if(jacobians[0] != NULL)
{
double S1 = parameters[0][0];
double S2 = parameters[0][1];
double S3 = parameters[0][2];
double K1 = parameters[0][3];
double K2 = parameters[0][4];
double K3 = parameters[0][5];
double b1 = parameters[0][6];
double b2 = parameters[0][7];
double b3 = parameters[0][8];
double A1 = sample_(0);
double A2 = sample_(1);
double A3 = sample_(2);
// 向量对向量的解析版:
Eigen::MatrixXd a(3, 1);
a << K1*(A1-b1), S1*K1*(A1-b1)+K2*(A2-b2), -S2*K1*(A1-b1)+S3*K2*(A2-b2)+K3*(A3-b3);
Eigen::MatrixXd da_dTheta(3, 9);
da_dTheta << 0, K1*(A1-b1), 0,
0, 0, -K1*(A1-b1),
0, 0, K2*(A2-b2),
A1-b1, S1*(A1-b1), -S2*(A1-b1),
0, A2-b2, S3*(A2-b2),
0, 0, A3-b3,
-K1, -S1*K1, S2*K1,
0, -K2, -S3*K2,
0, 0 ,-K3;
Eigen::Map<Eigen::Matrix<double, 1, 9, Eigen::RowMajor> > Jacob(jacobians[0]);
Jacob.setZero();
// 经过化简后,
// J = - (a / ||a||) * da_dTheta
// Jacob = - a.transpose() / a.norm() * da_dTheta;
Jacob = - calib_samp.transpose() / calib_samp.norm() * da_dTheta;
}
}
return true;
}
protected:
const _T1 g_mag_;
const Eigen::Matrix< _T1, 3 , 1> sample_;
};
大师兄:上面的代码其实是错误的,跟我公式里面打出来的完全不一样。为啥呢?
小红薯: 哦!是不是因为Eigen Matrix << 输入是横着的!你按竖着的输入了。
大师兄:对!所以正确代码如下:
template <typename _T1>
class MultiPosAccResidual_Analytical : public ceres::SizedCostFunction<1, 9> {
public:
MultiPosAccResidual_Analytical(const _T1 &g_mag, const Eigen::Matrix< _T1, 3 , 1> &sample
) : g_mag_(g_mag), sample_(sample){
}
virtual bool Evaluate(double const* const* parameters,
double* residuals,
double** jacobians) const
{
Eigen::Matrix<double, 3, 1> raw_samp(
double(sample_(0)),
double(sample_(1)),
double(sample_(2))
);
/* Apply undistortion transform to accel measurements
mis_mat_ << _T(1) , -mis_yz , mis_zy ,
mis_xz , _T(1) , -mis_zx ,
-mis_xy , mis_yx , _T(1) ; */
CalibratedTriad_<double> calib_triad(
//
// TODO: implement lower triad model here
//
// mis_yz, mis_zy, mis_zx:
double(0), double(0), double(0),
// mis_xz, mis_xy, mis_yx:
parameters[0][0], parameters[0][1], parameters[0][2],
// s_x, s_y, s_z:
parameters[0][3], parameters[0][4], parameters[0][5],
// b_x, b_y, b_z:
parameters[0][6], parameters[0][7], parameters[0][8]
);
// apply undistortion transform:
Eigen::Matrix< double, 3 , 1> calib_samp = calib_triad.unbiasNormalize( raw_samp );
residuals[0] = g_mag_*g_mag_ - calib_samp.transpose()*calib_samp;
// residuals[0] = g_mag_- calib_samp.norm();
if(jacobians != NULL)
{
if(jacobians[0] != NULL)
{
double S1 = parameters[0][0];
double S2 = parameters[0][1];
double S3 = parameters[0][2];
double K1 = parameters[0][3];
double K2 = parameters[0][4];
double K3 = parameters[0][5];
double b1 = parameters[0][6];
double b2 = parameters[0][7];
double b3 = parameters[0][8];
double A1 = sample_(0);
double A2 = sample_(1);
double A3 = sample_(2);
// 向量对向量的解析版:
Eigen::MatrixXd a(3, 1);
a << K1*(A1-b1), S1*K1*(A1-b1)+K2*(A2-b2), -S2*K1*(A1-b1)+S3*K2*(A2-b2)+K3*(A3-b3);
Eigen::MatrixXd da_dTheta(3, 9);
da_dTheta << 0, 0, 0, A1-b1, 0, 0, -K1, 0, 0,
K1*(A1-b1), 0, 0, S1*(A1-b1), A2-b2, 0, -S1*K1, -K2, 0,
0, -K1*(A1-b1), K2*(A2-b2), -S2*(A1-b1), S3*(A2-b2), A3-b3, S2*K1, -S3*K2, -K3;
Eigen::Map<Eigen::Matrix<double, 1, 9, Eigen::RowMajor> > Jacob(jacobians[0]);
Jacob.setZero();
// 经过化简后,
// J = - (a / ||a||) * da_dTheta
// Jacob = - a.transpose() / a.norm() * da_dTheta;
// Jacob = - calib_samp.transpose() / calib_samp.norm() * da_dTheta;
Jacob = - 2 * calib_samp.transpose() * da_dTheta;
}
}
return true;
}
protected:
const _T1 g_mag_;
const Eigen::Matrix< _T1, 3 , 1> sample_;
};
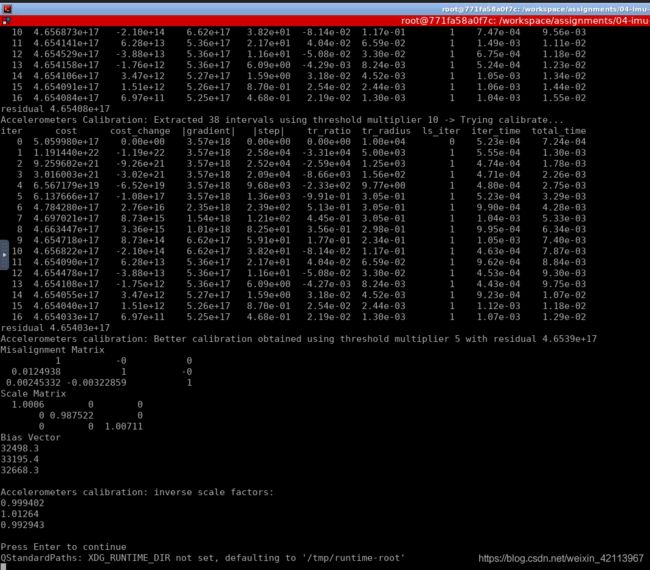
最后结果,如果代码用的residual是取平方的,Residual大概在50-70之间:
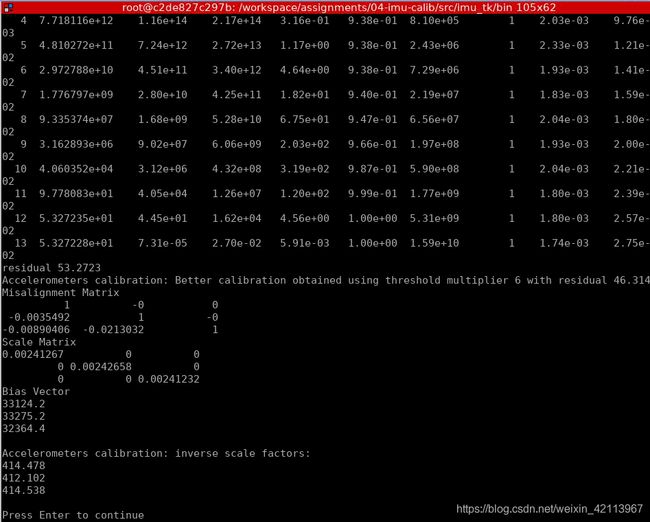
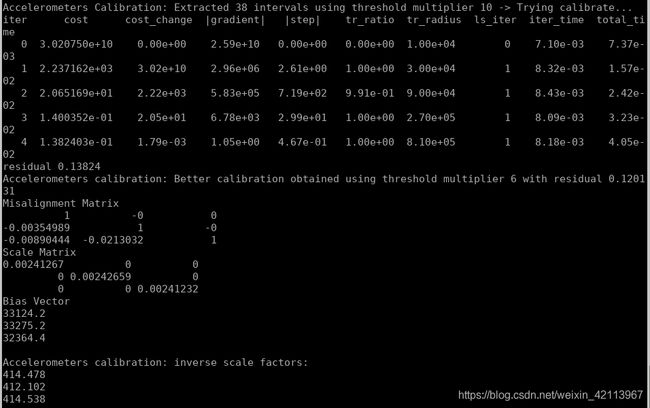
如果Residual不取平方,那大概residual大概在0.1左右:
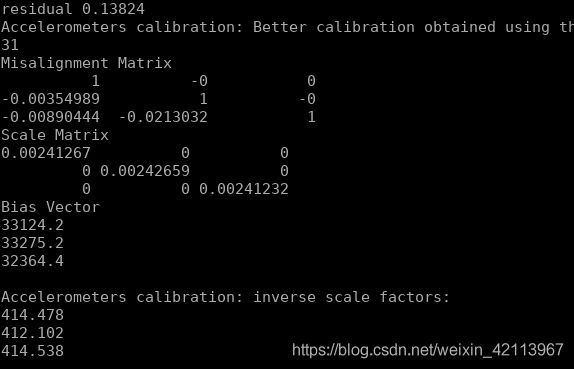
IMU内参Calibration的结果符合预期,完美收官!