打了一个补丁-有效的完全平方数-C语言

对于LeetCode第367题:有效的完全平方数

解法一：暴力遍历

由于int类型所能表示的最大数INT_MAX：2³¹-1，即2147483647
而$\sqrt{2147483647}$ $\approx$ 46340.950001
故在 [1，INT_MAX] 范围内的最大完全平方数的算术平方根为46340
所以暴力遍历代码如下：

#include
bool isPerfectSquare(int num);
int main()
{
     
	int n;
	while(scanf("%d",&n)==1)
		printf("%d\n",isPerfectSquare(n));
}
bool isPerfectSquare(int num)
{
     
	int i;
	for(i=1;i<=46340;i++)
		if(i*i==num)
			return true;//若i*i==num,说明num是完全平方数 
		else if(i*i>num)
			return false;//说明此时(i-1)*(i-1)
	return false;//针对num∈(46340*46340,INT_MAX]的情况 
}

这里要注意的是若 num > 2147395600 （即 46340*46340 ），i 会遍历完 1~43640 的每一个整数，然后退出循环，返回false。（因为46341*46341>INT_MAX，所以区间 (2147395600，INT_MAX] 的数肯定不是完全平方数）
暴力遍历虽然思路清晰，但是对于一个很大的数(不超过INT_MAX)却要计算成千上万次，白白浪费了时间（虽然计算机对于这点计算量还是不在话下的嘿嘿 ），下面给出时间复杂度更小的二分法

解法二：二分法

#include
bool isPerfectSquare(int num);
int main()
{
     
	int n;
	while(scanf("%d",&n)==1) 
		printf("The answer is %d\n",isPerfectSquare(n));
}
bool isPerfectSquare(int num)
{
     
	int left=1,right=num,mid=num/2;
	while(left<=right)
	{
     
		
		if(mid*mid<num)
		{
     
			left=mid+1;
			mid=(left+right)/2;
		}
		else if(mid*mid>num)
		{
     
			right=mid-1;
			mid=(left+right)/2;
		}
		else if(mid*mid==num)
			return true;
	}
	return false;
}

这是力扣题解里面写的最多的一种解法(这段代码是我自己写的，和其他人思路一样，并未抄袭)，但这段代码其实是有漏洞的，问题就在于 mid*mid 可能会数据溢出，也就是说 mid 不能超过46340，这就导致了输入的 n 不能超过46340*2+1=92681，也就是说这段代码只能正确计算 [1,92681] 范围内的数，其他正整数则会由于 mid*mid 的数据溢出而出现计算错误。
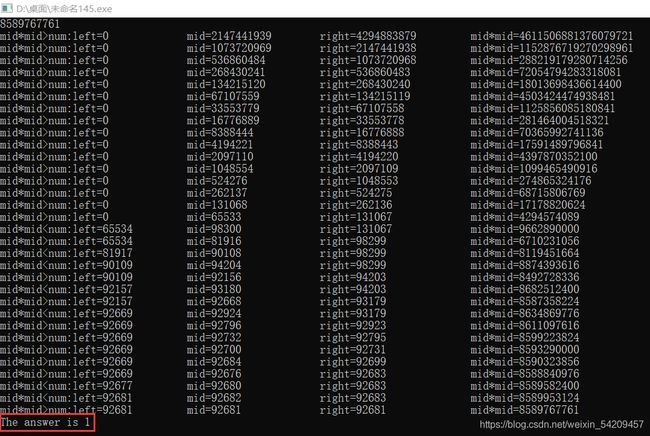
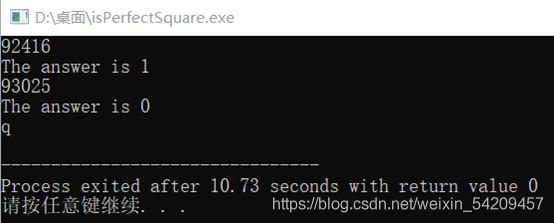
用Dev-C++用这段代码测试 92416 与 93025 两个数据
92416=304*304
93025=305*305
测试结果如下：

由于

	字节	整数最大值
int	4	231-1
long long	8	263-1
unsigned long long	8	264-1
double	8	21024

所以解决这个办法的最简单方法就是在 mid*mid 前面加一个1.0，1ll或者1ull转换下类型

代码如下

#include
bool isPerfectSquare(int num);
int main()
{
     
	int n;
	while(scanf("%d",&n)==1) 
		printf("The answer is %d\n",isPerfectSquare(n));
}
bool isPerfectSquare(int num)
{
     
	int left=1,right=num,mid=num/2;
	while(left<=right)
	{
     
		
		if(1.0*mid*mid<num)//1.0也可以换成1ll或者1ull 
		{
     
			left=mid+1;
			mid=(left+right)/2;
		}
		else if(1.0*mid*mid>num)//1.0也可以换成1ll或者1ull
		{
     
			right=mid-1;
			mid=(left+right)/2;
		}
		else if(mid*mid==num)//这里不用加 
			return true;
	}
	return false;
}

在 LeetCode 里面提交答案的结果如下

测试 92416，93025，2147395600 结果如下

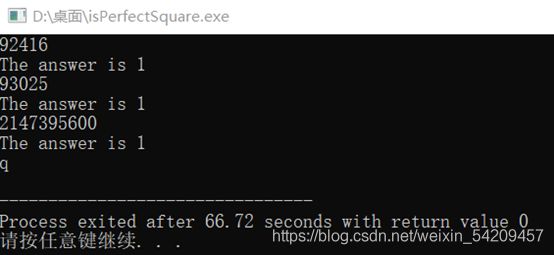
所以对于此题就完美解决了

举一反三

拓展一下本题，如果想要扩大能够输入的数的范围，继续判断这个数是不是完全平方数，怎么办？
其实也挺简单的，把变量 n，left , right , mid 都声明为 long long 或者
unsigned long long 或者 double 类型来扩大这些变量能表示的最大范围。但是由于这些类型还是有最大值，所以不可能正确计算无限大的数是不是完全平方数，对于unsigned long long ，我用以下代码（判断语句里面加了 printf 用来测试）测试了下

#include
bool isPerfectSquare(unsigned long long num);
int main()
{
     
	unsigned long long n;
	while(scanf("%llu",&n)==1)
		printf("The answer is %d\n",isPerfectSquare(n));
}
bool isPerfectSquare(unsigned long long num)
{
     
	unsigned long long left=0,right=num,mid=num/2;
	while(left<=right)
	{
     
		
		if(mid*mid<num)//这里就不用加ull了，因为前面已经声明了这些变量是ull类型 
		{
     
			left=mid+1;
			mid=(left+right)/2;
			printf("mid*mid,left,mid,right,mid*mid);
		}
		else if(mid*mid>num)
		{
     
			right=mid-1;
			mid=(left+right)/2;
			printf("mid*mid>num:left=%-10llu    mid=%-15llu   right=%-15llu    mid*mid=%-30llu\n",left,mid,right,mid*mid);
		}
		else if(mid*mid==num)
			return true;
	}
	return false;
}

因为 4294967295<$\sqrt{2^{64}-1}$<2³²=4294967296
故同样为了防止数据溢出，用这种方法所能计算的最大的数是
4294967295*2+1=8589934591(85亿多)

因为$\sqrt{8589934591}$ $\approx$ 92681.90018

92681*92681=8589767761
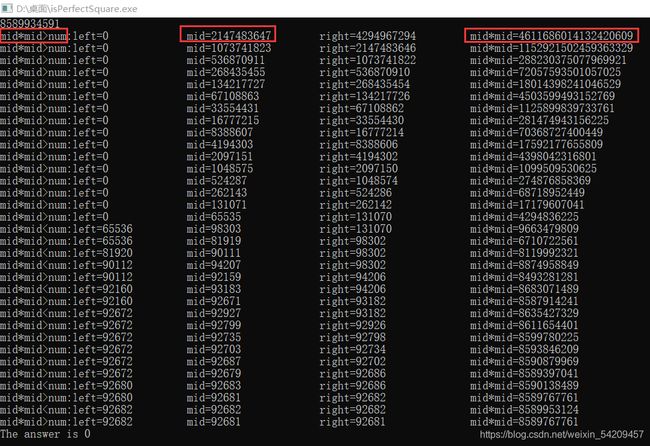
故用 8589767761 测试

测试结果如下:

用8589934591测试结果如下

2147483647*2147483647=4611686014132420609，并未发生数据溢出

用 8589934592 测试如下

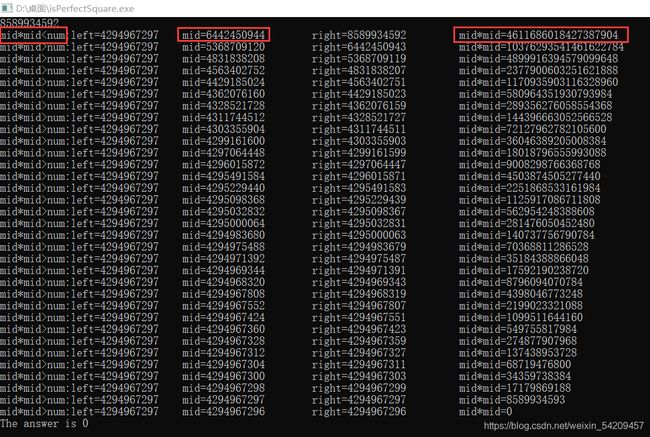
明显错误，第一次 mid * mid 肯定大于 num，其次这里 mid * mid 结果也不对，mid 的个位数为4，那么 mid * mid 的个位数必然为6，这说明 mid * mid溢出了。

另外，有人会问 double 类型所能表示最大整数为 2¹⁰²⁴，几乎是无穷大的数了，是不是可以用 double 来计算比 unsigned long long 更大范围的数呢？

我们把 unsigned long long 全部换成 double 测试一下

#include
bool isPerfectSquare(double num);
int main()
{
     
	double n;
	while(scanf("%lf",&n)==1)
		printf("%d\n",isPerfectSquare(n));

}
bool isPerfectSquare(double num)
{
     
	double left=0,right=num,mid=num/2;
	while(left<=right)
	{
     
		
		if(mid*mid<num)
		{
     
			left=mid+1;
			mid=(left+right)/2;
			printf("mid*mid,left,mid,right,mid*mid);
		}
		else if(mid*mid>num)
		{
     
			right=mid-1;
			mid=(left+right)/2;
			printf("mid*mid>num：left=%-10.0lf  mid=%-15.0lf  right=%-15.0lf  mid*mid=%-30.0lf\n",left,mid,right,mid*mid);
		}
		else if(mid*mid==num)
			return true;
	}
	return false;
}

当 n = 92681 * 92681 = 8589767761，测试结果如图

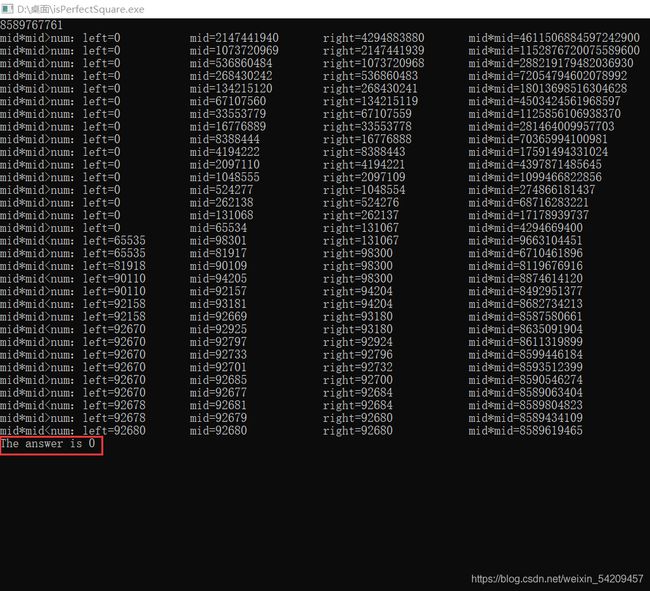
很明显 这里计算错误
2147441940*2147441940的准确结果是
4611506885670963600
而这里的结果是
4611506884597242900

我们对比一下
4611506885670963600
4611506884597242900

他这里第10位出现了不同，说明第11位及以后是不准确的，这也就是为什么这里answer是0 的原因
double虽然能表示的最大数是2¹⁰²⁴，但double的精度只有15-16位有效数字，超过这个位数就不准确了，所以会出现计算错误的情况。
PS：这里有点小问题就是既然double精度能达到15-16位，为啥这里只到第11位就不准确了，但我单独用2147441940测试的时候可以达到16位精度

#include
int main()
{
     
	double n=2147441940; 
	printf("%.0f",n*n); 
}

对比结果
4611506885670963600
4611506885670963700

这里到第17位才不同，这里我有点搞不懂！
俺同学叫我参考参考IEEE754
和这本书：提取码为1234

要结束啦

所以别看 double 能表示的最大整数比 unsigned long long 很大，但由于精度限制，能计算的最大值却没有 unsigned long long 大。另外,对于 double 或者 unsigned long long 数据其实也可以用第一种方法，计算出对应类型最大值的算术平方根（取整数），虽然可能要循环好多好多次，但是这种方法是最安全的！
所以如果你还想计算比 unsigned long long 能计算的数还大的数，或者无限大整数，就转战Python 吧！
因为在 Python 中，整数的值不受位数限制，并且可以扩展到可用内存的限制。也就是说你内存有多大，你就可以用多大的数字。因此，我们不需要任何特殊的安排来存储大量数字。

最后欢迎大家指出本文的可能出现的错误以及不足~